Расчет разветвленной параллельной RLC-цепи

Содержание страницы

1. Теоретические основы параллельной RLC-цепи
2. Векторные диаграммы и проводимости
3. Мощность в разветвленной цепи
4. Практические примеры расчета
5. Сравнение последовательной и параллельной RLC-цепей
6. Преимущества и недостатки параллельного соединения RLC
7. Интересные факты об RLC-цепях
8. FAQ: Часто задаваемые вопросы
Заключение

Разветвленная RLC-цепь (или параллельный колебательный контур) — это фундаментальная схема в электротехнике, состоящая из резистора, катушки индуктивности и конденсатора, соединенных параллельно.

История изучения таких цепей восходит к концу XIX века и работам Оливера Хевисайда и Чарльза Штейнмеца, которые разработали математический аппарат для анализа переменных токов. Понимание процессов в RLC-цепях необходимо для проектирования фильтров, усилителей и систем передачи энергии. В данной статье мы подробно разберем методы расчета, векторные диаграммы и решим практические задачи.

1. Теоретические основы параллельной RLC-цепи

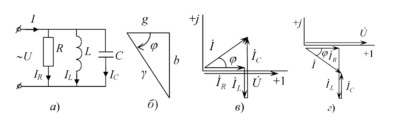
Простейшая разветвленная цепь, составленная из реальных элементов (резисторов, индуктивных катушек, конденсаторов), может быть представлена эквивалентной схемой из идеальных элементов \( R \), \( L \), \( C \), соединенных параллельно.

Рис. 1. Схема параллельной RLC-цепи (эквивалентная схема)

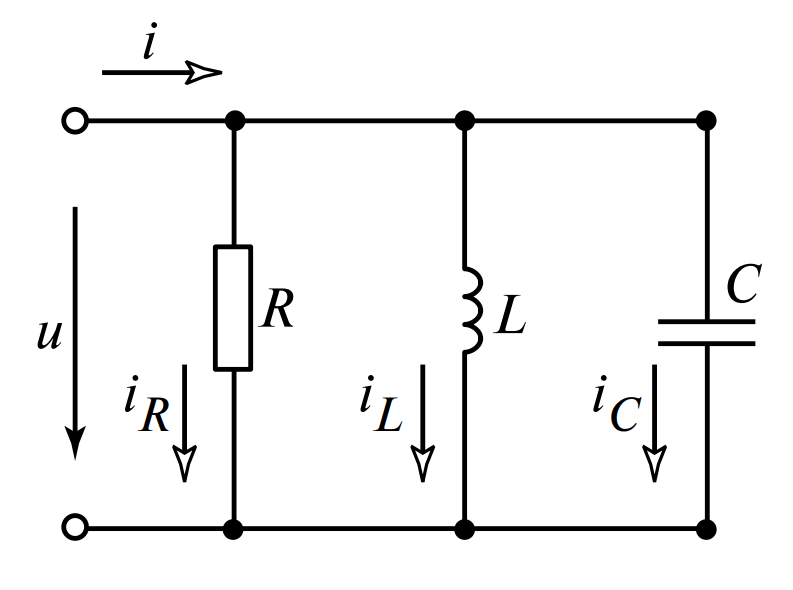
Общий ток \( i(t) \) по первому закону Кирхгофа равен сумме токов в ветвях:

i(t) = i_R + i_L + i_C = G u + \frac{1}{L} \int u \, dt + C \frac{du}{dt}

Здесь учтено, что токи в ветвях определяются следующими соотношениями:

Ток в резисторе: \( i_R = \frac{u}{R} = G u \) (где \( G \) — активная проводимость).
Ток в индуктивности: \( i_L = \frac{1}{L} \int u \, dt \).
Ток в емкости: \( i_C = C \frac{du}{dt} \).

Заметим, что зависимость тока \( i \) от напряжения \( u \) в рассматриваемой цепи описывается интегро-дифференциальным уравнением. При произвольной форме напряжения его решение сложно. Однако, в случае синусоидального напряжения эту сложность преодолеть легче.

Анализ при синусоидальном напряжении

Итак, пусть напряжение \( u \) будет синусоидальным: \( u(t) = U_m \sin \omega t \). Для простоты начальная фаза напряжения \( \psi_u \) принята равной нулю. Тогда токи в ветвях примут вид:

i_R = G U_m \sin \omega t = I_{Rm} \sin \omega t \) \( i_L = B_L U_m \sin(\omega t — \frac{\pi}{2}) = I_{Lm} \sin(\omega t — \frac{\pi}{2}) \) \( i_C = B_C U_m \sin(\omega t + \frac{\pi}{2}) = I_{Cm} \sin(\omega t + \frac{\pi}{2})

где \( B_L = \frac{1}{\omega L} \) — индуктивная проводимость, а \( B_C = \omega C \) — емкостная проводимость.

2. Векторные диаграммы и проводимости

Изложенное выше позволяет изобразить векторную диаграмму. Она строится для действующих значений токов и напряжений:

I_R = G U; \quad I_L = B_L U; \quad I_C = B_C U

В векторной форме общее уравнение токов выглядит так: \( \vec{I} = \vec{I}_R + \vec{I}_L + \vec{I}_C \).

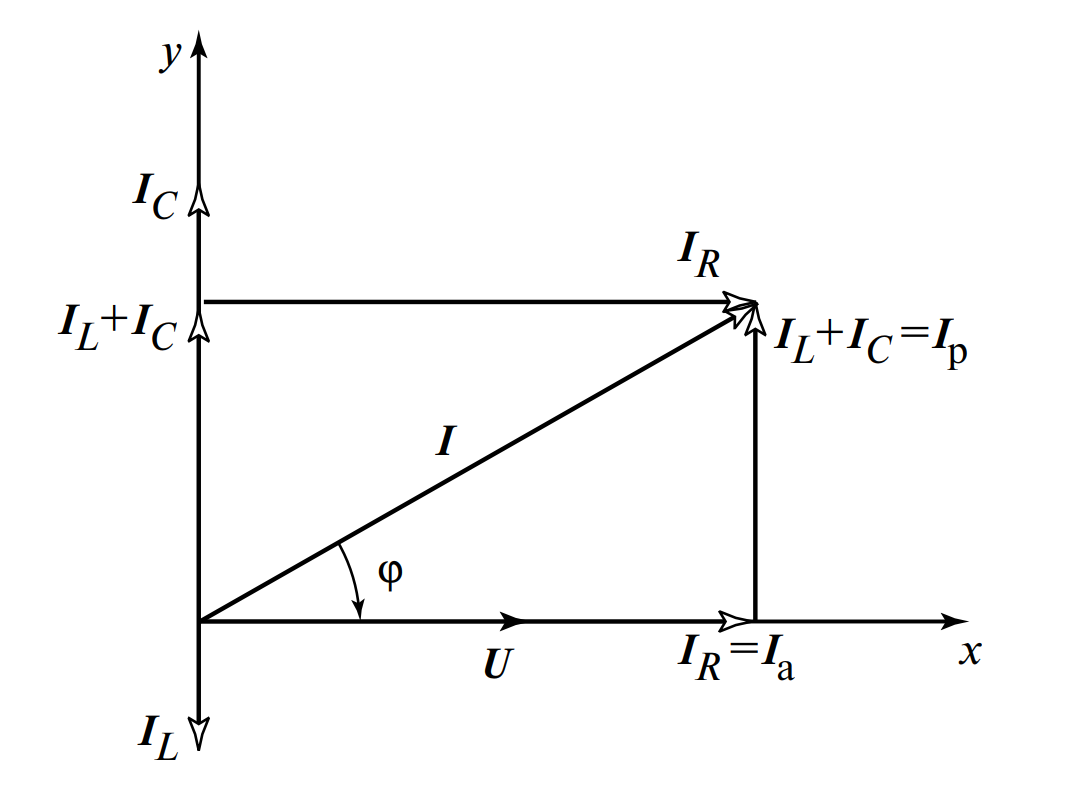
Рис. 2. Векторная диаграмма токов параллельной RLC-цепи

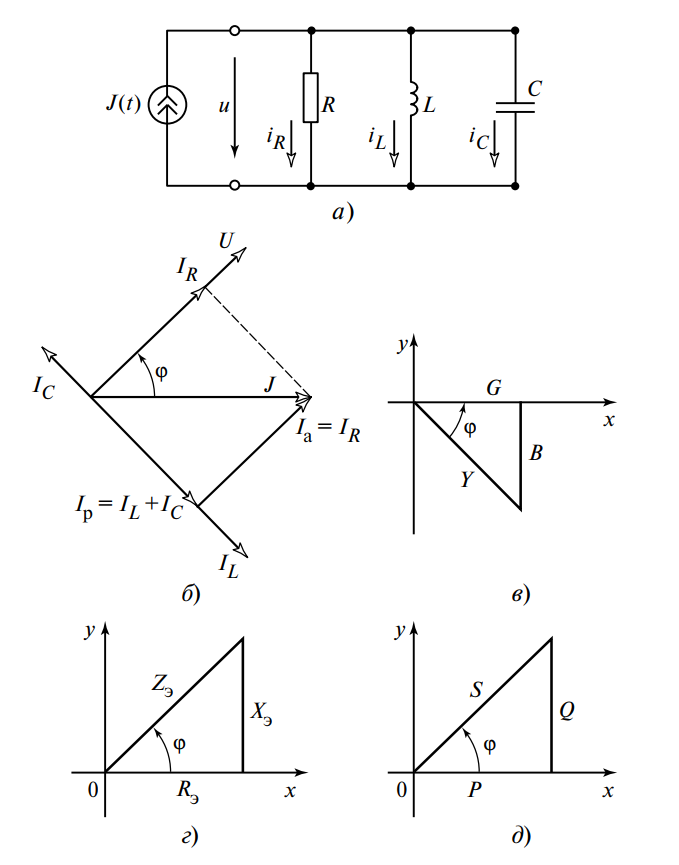
На рис. 2 видно, что векторы \( \vec{I}_L \) и \( \vec{I}_C \) направлены в противоположные стороны, т.е. находятся в противофазе. Поэтому их результирующая (реактивная составляющая тока) равна:

\( I_p = I_L — I_C \)

Здесь \( I_p \) — реактивная составляющая общего тока \( I \), направленная перпендикулярно вектору напряжения \( U \), в отличие от активной составляющей \( I_a \), направленной по вектору напряжения \( U \). Очевидно, что \( I_a = I_R \).

Векторы \( \vec{I} \), \( \vec{I}_a \) и \( \vec{I}_p \) образуют треугольник токов, из которого можно определить действующее значение общего тока:

I = \sqrt{I_a^2 + I_p^2} = \sqrt{(GU)^2 + (I_L — I_C)^2} = U \sqrt{G^2 + (B_L — B_C)^2} = U \sqrt{G^2 + B^2} = YU

где:

\( B = B_L — B_C \) — реактивная проводимость цепи;
\( Y = \sqrt{G^2 + B^2} \) — полная проводимость RLC-цепи.

Сдвиг фаз \( \phi \) между током \( i \) и напряжением \( u \) можно определить из треугольника токов:

\operatorname{tg} \phi = \frac{I_p}{I_a} = \frac{I_L — I_C}{I_R} = \frac{B_L — B_C}{G} = \frac{B}{G}

Характер цепи

Реактивная проводимость \( B \) и сдвиг по фазе \( \phi \) могут быть больше или меньше нуля в зависимости от соотношения величин \( B_L \) и \( B_C \). При этом \( -\pi/2 \le \phi \le \pi/2 \).

Если \( B > 0 \) (\( B_L > B_C \)), то говорят, что цепь носит активно-индуктивный характер (ток отстает от напряжения).
Если \( B < 0 \) (\( B_L < B_C \)), то цепь активно-емкостная (ток опережает напряжение).

Иногда цепь характеризуют треугольником проводимостей \( G, B, Y \). Так как \( I_a = GU \), \( I_p = BU \), \( I = YU \), то треугольник проводимостей подобен треугольнику токов.

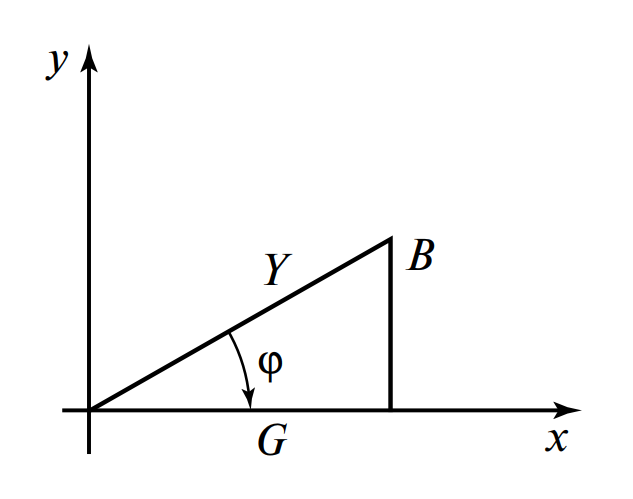
Рис. 3. Треугольник проводимостей

В итоге мгновенное значение общего тока цепи:

i(t) = I_m \sin(\omega t — \phi)

Где амплитуда тока \( I_m = Y U_m \), а угол \( \phi = \operatorname{arctg}(\frac{B_L — B_C}{G}) \).

3. Мощность в разветвленной цепи

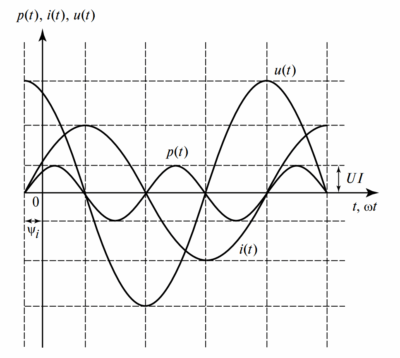
Мгновенная мощность определяется выражением:

p(t) = u(t)i(t) = U_m I_m \sin \omega t \sin(\omega t — \phi) = UI \cos \phi — UI \cos(2\omega t — \phi)

Она состоит из двух составляющих:

Постоянной величины \( P = UI \cos \phi \) (активная мощность).
Переменной \( UI \cos(2\omega t — \phi) \), имеющей удвоенную частоту по сравнению с частотой тока и напряжения.

График \( p(t) \) для разветвленной цепи будет иметь такой же вид, как и для последовательной RLC-цепи, но с учетом фазовых сдвигов.

Рис. 4. Треугольники сопротивлений (а) и мощностей (б)

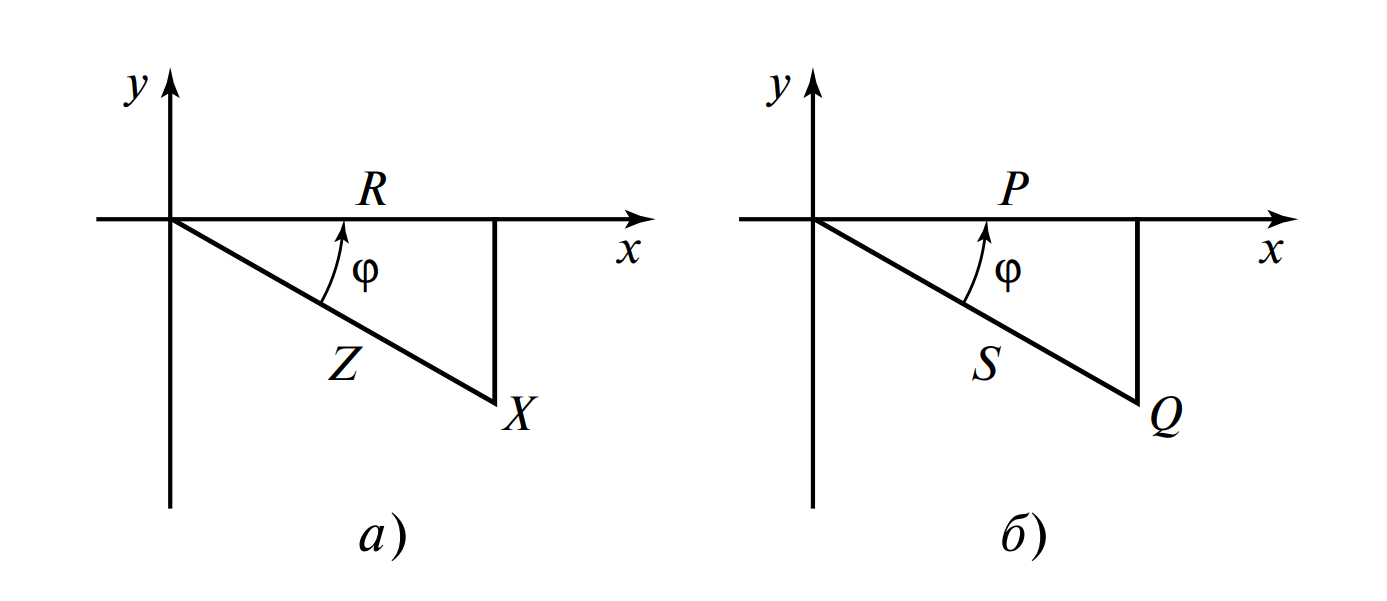
Рисунок 4 приведен для того, чтобы подчеркнуть, что любой двухполюсник, содержащий параллельные RLC-элементы, может быть охарактеризован не только проводимостями, но и эквивалентными сопротивлениями. При этом полное сопротивление \( Z_э = 1/Y \), \( R_э = Z_э \cos \phi \), \( X_э = Z_э \sin \phi \).

4. Практические примеры расчета

Пример 1 (Исходная задача 9.3)

Дано: Параллельную RLC-цепь питает источник тока \( J(t) = 20 \sin 2000t \) А. Параметры элементов: \( R = 10 \) Ом, \( L = 0,004 \) Гн, \( C = 12,5 \) мкФ.

Требуется: Определить характер цепи. Рассчитать напряжение на зажимах источника, токи в ветвях, активную, реактивную, комплексную мощности, коэффициент мощности. Построить векторные диаграммы и треугольники.

Решение:

1. Изобразим расчетную схему (рис. 5, а), укажем на ней положительные направления токов и напряжения.

2. Найдем проводимости ветвей:

Активная проводимость: \( G = 1/R = 1/10 = 0,1 \) См.
Индуктивная проводимость: \( B_L = \frac{1}{\omega L} = \frac{1}{2000 \cdot 0,004} = 0,125 \) См.
Емкостная проводимость: \( B_C = \omega C = 2000 \cdot 12,5 \cdot 10^{-6} = 0,025 \) См.
Реактивная проводимость: \( B = B_L — B_C = 0,125 — 0,025 = 0,1 \) См.
Полная проводимость: \( Y = \sqrt{G^2 + B^2} = \sqrt{0,1^2 + 0,1^2} \approx 0,141 \) См.

Найдем сдвиг фаз:

\phi = \operatorname{arctg} \frac{B}{G} = \operatorname{arctg} \frac{0,1}{0,1} = 45^\circ

Так как \( B > 0 \), то цепь носит активно-индуктивный характер.

3. Амплитуда напряжения: \( U_m = J_m / Y = 20 / 0,141 \approx 141 \) В.

4. Амплитуды токов:

\( I_{Rm} = G U_m = 0,1 \cdot 141 = 14,1 \) А.
\( I_{Lm} = B_L U_m = 0,125 \cdot 141 = 17,625 \) А.
\( I_{Cm} = B_C U_m = 0,025 \cdot 141 = 3,525 \) А.

Рис. 5. Расчетная схема (а), треугольники токов (б), проводимостей (в), сопротивлений (г) и мощностей (д) для Примера 1

5. Мгновенные значения напряжения и токов:

\( u(t) = 141 \sin(2000t + 45^\circ) \) В (так как ток источника мы взяли за базу с нулевой фазой, а напряжение опережает ток в индуктивной цепи, фаза напряжения будет +45°).
\( i_R(t) = 14,1 \sin(2000t + 45^\circ) \) А (совпадает по фазе с \( u(t) \)).
\( i_L(t) = 17,625 \sin(2000t — 45^\circ) \) А (отстает от \( u(t) \) на 90°).
\( i_C(t) = 3,525 \sin(2000t + 135^\circ) \) А (опережает \( u(t) \) на 90°).

6. Мощности:

Полная мощность: \( S = \frac{U_m J_m}{2} = \frac{141 \cdot 20}{2} = 1410 \) В·А = 1,41 кВ·А.
Активная мощность: \( P = S \cos \phi = 1410 \cos 45^\circ = 1000 \) Вт = 1 кВт.
Реактивная мощность: \( Q = S \sin \phi = 1410 \sin 45^\circ = 1000 \) вар = 1 квар.

7. Коэффициент мощности: \( \cos \phi = G / Y = P / S \approx 0,707 \).

8. Эквивалентные сопротивления:

Полное сопротивление: \( Z = 1/Y \approx 7,07 \) Ом.
Активное сопротивление эквивалентной последовательной схемы: \( R_э = Z \cos \phi = 5 \) Ом.
Реактивное сопротивление эквивалентной последовательной схемы: \( X_э = Z \sin \phi = 5 \) Ом.

Пример 2 (Модифицированная задача)

Условие: Решить предыдущую задачу, приняв \( L = 20 \) мГн, \( C = 50 \) мкФ.

Решение:

1. Вычисляем новые проводимости:

\( G = 0,1 \) См (без изменений).
\( B_L = \frac{1}{2000 \cdot 0,02} = \frac{1}{40} = 0,025 \) См.
\( B_C = 2000 \cdot 50 \cdot 10^{-6} = 0,1 \) См.

2. Реактивная проводимость цепи:

\( B = B_L — B_C = 0,025 — 0,1 = -0,075 \) См.

Так как \( B < 0 \), цепь носит активно-емкостный характер.

3. Полная проводимость:

\( Y = \sqrt{0,1^2 + (-0,075)^2} = \sqrt{0,01 + 0,005625} = \sqrt{0,015625} = 0,125 \) См.

4. Напряжение на зажимах:

\( U_m = \frac{J_m}{Y} = \frac{20}{0,125} = 160 \) В.

Это пример показывает, как изменение параметров реактивных элементов кардинально меняет характер нагрузки с индуктивного на емкостный.

5. Сравнение последовательной и параллельной RLC-цепей

Характеристика	Последовательная RLC-цепь	Параллельная RLC-цепь
Основной закон	Второй закон Кирхгофа (сложение напряжений)	Первый закон Кирхгофа (сложение токов)
Общий параметр	Ток \( I \) одинаков для всех элементов	Напряжение \( U \) одинаково для всех элементов
Резонанс	Резонанс напряжений (возможно \( U_L, U_C > U_{вх} \))	Резонанс токов (возможно \( I_L, I_C > I_{вх} \))
Условие резонанса	\( \omega L = \frac{1}{\omega C} \) (или \( X_L = X_C \))	\( \frac{1}{\omega L} = \omega C \) (или \( B_L = B_C \))
Импеданс при резонансе	Минимальный (\( Z_{min} = R \))	Максимальный (\( Z_{max} = R \))
Применение	Входные цепи радиоприемников (последовательный фильтр)	Контуры гетеродинов, выходные каскады передатчиков (фильтр-пробка)

6. Преимущества и недостатки параллельного соединения RLC

Преимущества:

Независимость работы ветвей: выход из строя одного элемента не разрывает цепь полностью (в отличие от последовательного соединения).
Возможность получения резонанса токов, что позволяет «накачивать» большую энергию внутри контура при малом токе источника.
Удобство подключения к источникам напряжения (стандарт для электросетей).

Недостатки:

Сложность расчетов из-за необходимости оперировать проводимостями.
Риск перегрузки ветвей реактивными токами при резонансе, что может привести к тепловому пробою.

7. Интересные факты об RLC-цепях

Резонанс токов: Резонанс в параллельной цепи называется «резонансом токов», потому что токи между катушкой и конденсатором могут в десятки раз превышать ток, потребляемый от источника.
Свойства фильтра: Параллельный RLC-контур обладает свойствами полосового фильтра, пропуская только частоты, близкие к резонансной, если подключен последовательно нагрузке, или подавляя их при ином включении.
Добротность (Q): Добротность (Q-factor) определяет качество контура. Чем выше добротность, тем острее пик резонанса и дольше затухают колебания.
Диссипация энергии: В идеальном LC-контуре (без резистора) колебания продолжались бы вечно. Резистор \( R \) в нашей схеме отвечает за диссипацию (рассеивание) энергии в тепло.
Метод Штейнмеца: Концепция импеданса и комплексных чисел для расчета RLC-цепей была популяризирована Чарльзом Штейнмецем, что позволило заменить сложные дифференциальные уравнения простой алгеброй.
Компенсация мощности: В реальных высоковольтных сетях конденсаторы подключают параллельно нагрузке для компенсации реактивной мощности (power factor correction), уменьшая потери в проводах.
Паразитные эффекты: Паразитные емкости и индуктивности проводов создают непреднамеренные RLC-цепи, которые могут вызывать нежелательные «звоны» и помехи в электронике.

8. FAQ: Часто задаваемые вопросы

1. Почему токи в индуктивности и емкости имеют противоположные знаки в формуле реактивного тока?Это связано с физикой процессов: индуктивность сопротивляется изменению тока (ток отстает от напряжения на 90°), а емкость сопротивляется изменению напряжения (ток опережает напряжение на 90°). Разница фаз составляет 180°, то есть они находятся в противофазе.

2. Что произойдет, если \( B_L = B_C \)?Наступит резонанс токов. Реактивная проводимость цепи станет равной нулю, общий ток будет совпадать по фазе с напряжением и будет минимальным (равным \( I_R \)).

3. Можно ли рассчитывать параллельную цепь через сопротивления, а не проводимости?Да, можно, используя метод комплексных сопротивлений: \( Z_{экв} = \frac{1}{\frac{1}{R} + \frac{1}{j\omega L} + j\omega C} \). Однако метод проводимостей для параллельных цепей математически проще, так как позволяет складывать элементы, а не дроби.

4. В каких единицах измеряется проводимость?Проводимость измеряется в Сименсах (См). 1 См = 1 / Ом.

5. Опасен ли резонанс токов?Для источника питания он часто полезен (разгружает линию), но для элементов контура может быть опасен, если они не рассчитаны на высокие внутренние токи циркуляции.

Заключение

Расчет разветвленной RLC-цепи требует внимательного подхода к определению проводимостей ветвей и построению векторных диаграмм. Использование метода проводимостей значительно упрощает анализ параллельных соединений по сравнению с методом сопротивлений. Понимание поведения активной и реактивной составляющих тока позволяет инженерам эффективно компенсировать реактивную мощность и проектировать устойчивые резонансные системы. Мы рассмотрели теоретические основы, формулы и разобрали два численных примера, демонстрирующих изменение характера нагрузки при вариации параметров \( L \) и \( C \).

Нормативная база

При проектировании и оформлении схем следует руководствоваться действующими стандартами:

ГОСТ 2.702-2011 — Единая система конструкторской документации (ЕСКД). Правила выполнения электрических схем.
ГОСТ 2.728-74 — ЕСКД. Обозначения условные графические в схемах. Резисторы, конденсаторы.
ГОСТ 2.725-68 — ЕСКД. Обозначения условные графические в схемах. Устройства индуктивные и трансформаторы.
ГОСТ IEC 60050-131-2011 — Международный электротехнический словарь. Теория цепей.

Расчет разветвленной параллельной RLC-цепи: Расчет токов, мощности и векторные диаграммы