Электромагнитная совместимость и токи в экранах силовых кабелей

Содержание страницы

1. Расчет токов в экранах кабеля при двухстороннем заземлении
2. Напряжение на экранах кабеля: безопасность и изоляция
3. Методика выбора расчетных токов короткого замыкания
4. Интересные факты об экранах силовых кабелей
5. Часто задаваемые вопросы (FAQ)
Заключение

Развитие современных систем электроснабжения, в особенности в классах напряжения от 6 до 500 кВ, неразрывно связано с переходом от трехфазных кабелей с поясной изоляцией к однофазным кабелям с изоляцией из сшитого полиэтилена (СПЭ). Это технологическое решение обладает рядом неоспоримых преимуществ: высокой пропускной способностью, технологичностью монтажа, низкими диэлектрическими потерями и высокой надежностью. Однако конструктивная особенность однофазного исполнения порождает специфическую инженерную задачу — управление электромагнитными процессами в металлических экранах.

В отличие от трехжильного кабеля, где геометрическая сумма токов жил (в симметричном режиме) близка к нулю и результирующее магнитное поле за пределами общей оболочки минимально, одножильный кабель является мощным источником переменного магнитного поля. Это поле пересекает металлический экран как собственного кабеля, так и соседних фаз, индуцируя в них электродвижущую силу (ЭДС).

Аналогия: Представьте работу однофазного кабеля как работу трансформатора. Жила кабеля выступает в роли первичной обмотки, по которой течет большой ток нагрузки. Металлический экран кабеля играет роль одновитковой вторичной обмотки. Если замкнуть эту вторичную обмотку (заземлить экран с двух сторон), в ней, как и в трансформаторе, потечет значительный ток, который не совершает полезной работы, а лишь нагревает кабель, снижая его пропускную способность.

Игнорирование этих процессов на этапе проектирования может привести к фатальным последствиям: от перегрева изоляции и снижения срока службы линии до пробоя оболочки и поражения персонала электрическим током.

1. Расчет токов в экранах кабеля при двухстороннем заземлении

1.1. Физическая природа и математическая модель

Режим, при котором экраны кабельной линии (КЛ) заземлены с обоих концов, называется «Двухстороннее заземление экранов» или Solid Bonding. В этом случае контур для протекания тока замкнут через заземляющие устройства. Ток, протекающий в экране $ I_{Э} $, индуцируется магнитным полем тока жилы $ I_{Ж} $.

Величина этого тока прямо пропорциональна току в жиле. В инженерной практике для оценки эффективности работы кабельной системы и выбора сечения экрана удобнее оперировать не абсолютными амперами, а безразмерной величиной — коэффициентом (долей) тока в экране.

Относительный ток в экране определяется соотношением: $$ \frac{\dot{I}_{Э}}{\dot{I}_{Ж}} $$

Используя данные по погонным параметрам кабелей (активным и реактивным сопротивлениям), можно вывести выражение для расчета токов в экранах, заземленных по концам, для нормального режима работы сети.

В комплексной форме выражение имеет вид: $$ \frac{\dot{I}_{Э}}{\dot{I}_{Ж}} = — \frac{jX}{R_{Э} + jX} $$

Где:

$ R_{Э} $ — активное сопротивление экрана (Ом). Учитывается температурная зависимость сопротивления материала (медь, алюминий, свинец).
$ X $ — индуктивное сопротивление взаимоиндукции системы «жила-экран» (Ом).

Важно: В приведенной формуле в качестве $ R_{Э} $ и $ X $ можно использовать как полные значения сопротивлений для всей длины кабельной линии $ L_{К} $ (Ом), так и удельные значения на единицу длины (Ом/км). Результат отношения от этого не изменится, так как длина сокращается.

1.2. Определение индуктивного сопротивления

Индуктивное сопротивление $ X $ является ключевым фактором, определяющим величину паразитных токов. Оно зависит от геометрии прокладки кабелей. Для наиболее распространенных конфигураций формула выглядит следующим образом:

X = \omega L_{К} \frac{\mu_{0}}{2\pi} \left[ \ln\left(\frac{D}{r}\right) — \ln\left(\frac{D}{s}\right) \right] = \omega L_{К} \frac{\mu_{0}}{2\pi} \ln\left(\frac{s}{r}\right) \approx \omega L \frac{\mu_{0}}{2\pi} \ln\left(\frac{2s}{d_{Э}}\right)

Где:

$ \omega = 2\pi f $ — угловая частота сети (для 50 Гц $ \omega \approx 314 $ рад/с).
$ L_{К} $ — длина кабеля, м.
$ \mu_{0} $ — магнитная постоянная ($ 4\pi \times 10^{-7} $ Гн/м).
$ s $ — расстояние между осями соседних фаз кабелей (при прокладке треугольником) или среднее геометрическое расстояние.
$ d_{Э} $ — средний диаметр экрана, м. Следует учитывать, что он несколько больше наружного диаметра изоляции ($ 2r_{2} $).

Для практических расчетов часто требуется модуль величины тока, который позволяет выбрать сечение экрана по термической стойкости:

Формула 1: Модуль относительного тока в экране $$ \left| \frac{I_{Э}}{I_{Ж}} \right| = \frac{X}{\sqrt{R_{Э}^2 + X^2}} $$

1.3. Влияние способа прокладки: «Треугольник» vs «Плоскость»

Рассмотрим случай прокладки фаз кабеля вплотную друг к другу сомкнутым треугольником (в вершинах равностороннего треугольника). В этом случае расстояние между центрами жил $ s $ примерно равно диаметру кабеля по оболочке $ d $. С учетом того, что внешний диаметр $ d $ всегда больше среднего диаметра экрана $ d_{Э} $, отношение $ s/d_{Э} $ находится в диапазоне от 1 до 2.

Внимание: Классические формулы часто выводятся при допущении $ s \gg r_{2} $ (или $ s/d_{Э} \gg 0.5 $). При прокладке сомкнутым треугольником это условие выполняется «на грани» ($ s/d_{Э} \approx 1 \div 2 $). Поэтому результаты расчетов для такой конфигурации следует воспринимать как оценочные, имеющие определенную погрешность, однако достаточные для инженерного выбора оборудования.

Анализ формулы (1) позволяет сделать важные выводы о факторах, влияющих на токи в экранах:

Независимость от жилы: Ток в экране (в относительном выражении) не зависит от сечения самой жилы.
Независимость от длины: При условии однородности прокладки длина трассы не влияет на отношение токов.
Зависимость от экрана: Чем больше сечение экрана (меньше $ R_{Э} $), тем больше в нем ток. Это парадокс: улучшая экран, мы увеличиваем потери в нем при двухстороннем заземлении.
Геометрия: Увеличение расстояния $ s $ между фазами резко увеличивает индуктивное сопротивление $ X $ и, как следствие, ток в экране.

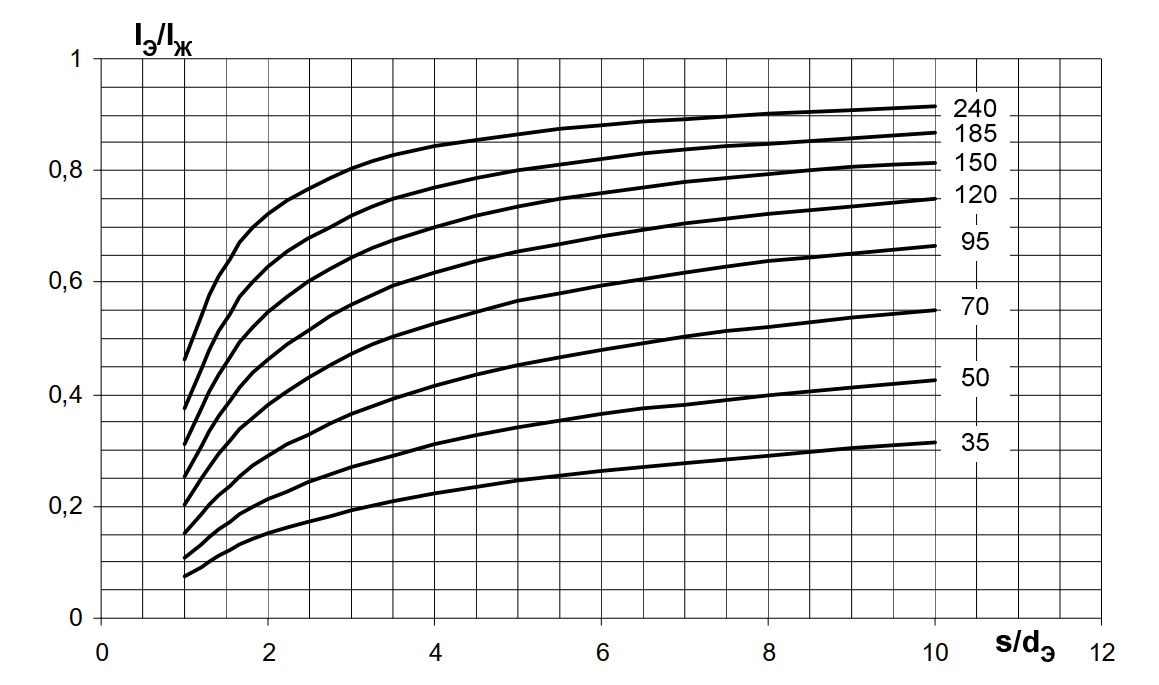
Рис. 1. Токи в заземленных по концам экранах трехфазной группы однофазных кабелей $ I_{Э} $ в зависимости от сечения экрана $ F_{Э} $ (мм²) и взаимного расположения фаз $ s/d_{Э} $.
Описание: На графике по оси абсцисс отложено отношение расстояния между фазами к диаметру экрана ($ s/d_{Э} $), по оси ординат — отношение тока экрана к току жилы. Представлено семейство кривых для различных сечений экрана (35, 50, 70, 95, 120, 150, 185, 240 мм²). Кривые показывают рост тока при увеличении расстояния между фазами и при увеличении сечения экрана.

Из анализа рисунка 1 следует, что для всех классов напряжения с увеличением сечения экрана $ F_{Э} $ и расстояния $ s $ токи в экранах возрастают. В неблагоприятных случаях (плоская прокладка с большим расстоянием между фазами, массивный экран) ток в экране может быть сопоставим с током жилы, что делает эксплуатацию линии экономически нецелесообразной из-за гигантских потерь. Приемлемые значения $ I_{Э}/I_{Ж} $ достигаются только при малых сечениях экрана и прокладке компактным треугольником.

2. Напряжение на экранах кабеля: безопасность и изоляция

2.1. Механизм возникновения перенапряжений

Если экран кабеля заземлен только с одной стороны (схема Одностороннее заземление экранов — Single Point Bonding), то контур для протекания индуктированного тока разомкнут. В этом случае на всей длине экрана наводится ЭДС относительно земли, достигающая максимума на разземленном конце. Это напряжение представляет прямую угрозу для персонала и внешней оболочки кабеля.

В соответствии с нормативными документами (ГОСТ Р 55025-2012, ПУЭ), напряжение на экране при нормальном режиме работы должно быть ограничено безопасными величинами (обычно не более 60-100 В в зависимости от условий доступа персонала).

2.2. Расчет напряжения в симметричном режиме

Для симметричного режима работы (прямой последовательности) напряжение на незаземленном конце определяется как падение напряжения на взаимной индуктивности:

\dot{U}_{Э} = (\dot{Z}_{ЖЭ} — \dot{Z}_{К}) \cdot \dot{I}_{Ж} \cdot L_{К}

После математических преобразований получаем упрощенную формулу:

\dot{U}_{Э} = jX^{*} \cdot \dot{I}_{Ж} \cdot L_{К}

Переходя к модулю величин (для практических измерений вольтметром):

Формула 2: Напряжение в нормальном режиме $$ U_{Э} = X^{*} \cdot I_{Ж} \cdot L_{К} $$

Где удельное индуктивное сопротивление $ X^{*} $ (Ом/км) рассчитывается как:

X^{*} = \omega \frac{\mu_{0}}{2\pi} \ln\left(\frac{s}{r}\right) = \omega \frac{\mu_{0}}{2\pi} \ln\left(\frac{2s}{d_{Э}}\right)

2.3. Расчет напряжения при коротких замыканиях

Наиболее критичным режимом является однофазное короткое замыкание (КЗ) во внешней сети. В этот момент через жилу протекают токи величиной в десятки килоампер, что приводит к возникновению на экране импульсов перенапряжения, способных пробить оболочку кабеля.

Напряжение на разземленном конце при КЗ: $$ \dot{U}_{Э} = \dot{Z}_{ЖЭ} \cdot \dot{I}_{К} \cdot L_{К} $$

Раскрывая полное сопротивление взаимоиндукции:

\dot{U}_{Э} = (R_{З}^{*} + j\omega M_{ЖЭ}^{*}) \cdot \dot{I}_{К} \cdot L_{К}

Поскольку активное сопротивление земли $ R_{З}^{*} $ пренебрежимо мало по сравнению с реактивной составляющей взаимоиндукции $ \omega M_{ЖЭ}^{*} $, формула упрощается до:

Формула 3: Напряжение при коротком замыкании $$ U_{Э} \approx X_{ЖЭ}^{*} \cdot I_{К} \cdot L_{К} $$

Где сопротивление взаимоиндукции «жила-экран» с учетом возврата тока через землю определяется как:

X_{ЖЭ}^{*} = \omega M_{ЖЭ}^{*} = \omega \frac{\mu_{0}}{2\pi} \ln\left(\frac{D_{З}}{r}\right) = \omega \frac{\mu_{0}}{2\pi} \ln\left(\frac{2D_{З}}{d_{Э}}\right)

Здесь $ D_{З} $ — эквивалентная глубина проникновения тока в землю, зависящая от удельного сопротивления грунта $ \rho_{З} $.

Анализ: Из формул (2) и (3) видно, что напряжение на экране зависит от:

Тока в жиле $ I_{Ж} $ (линейно).
Длины участка кабеля $ L_{К} $ (линейно) — именно поэтому длинные линии разбивают на секции транспозицией.
Геометрии прокладки $ s/d_{Э} $ (для нормального режима).
Свойств грунта и глубины прокладки (для режимов КЗ с возвратом тока через землю).

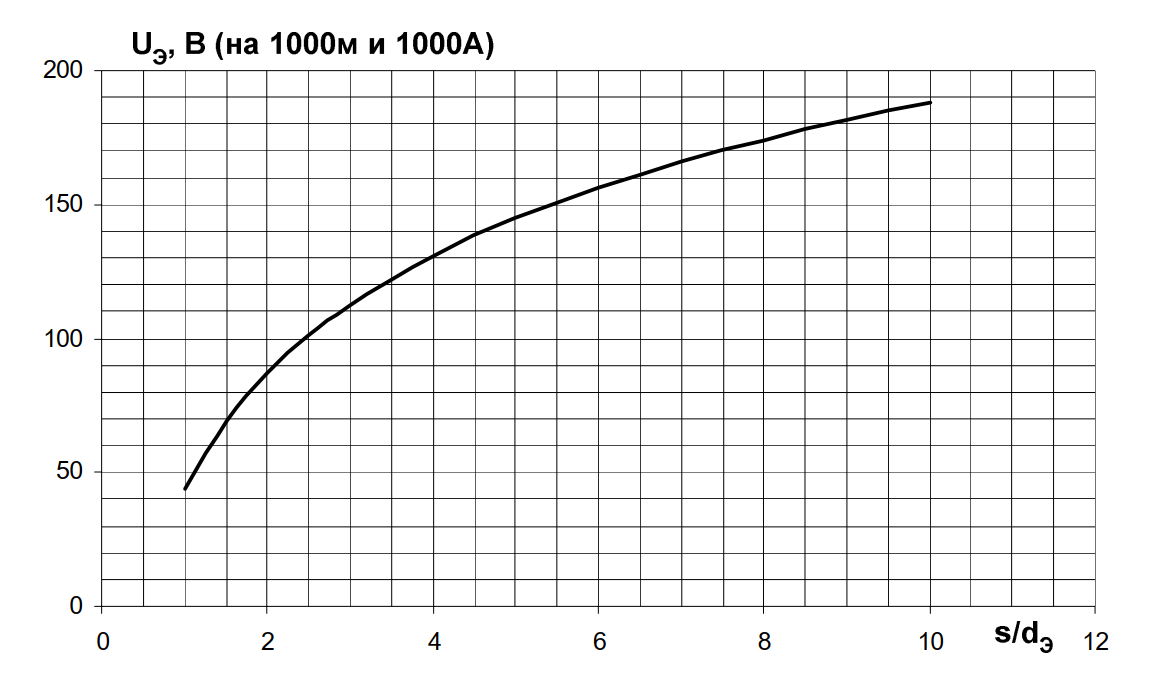
Рис. 2. Напряжение на экране кабеля 6-500 кВ относительно земли $ U_{Э} $, определенное по формуле (2) в зависимости от соотношения $ s/d_{Э} $ для кабеля длиной 1000 м при токе жилы 1000 А.

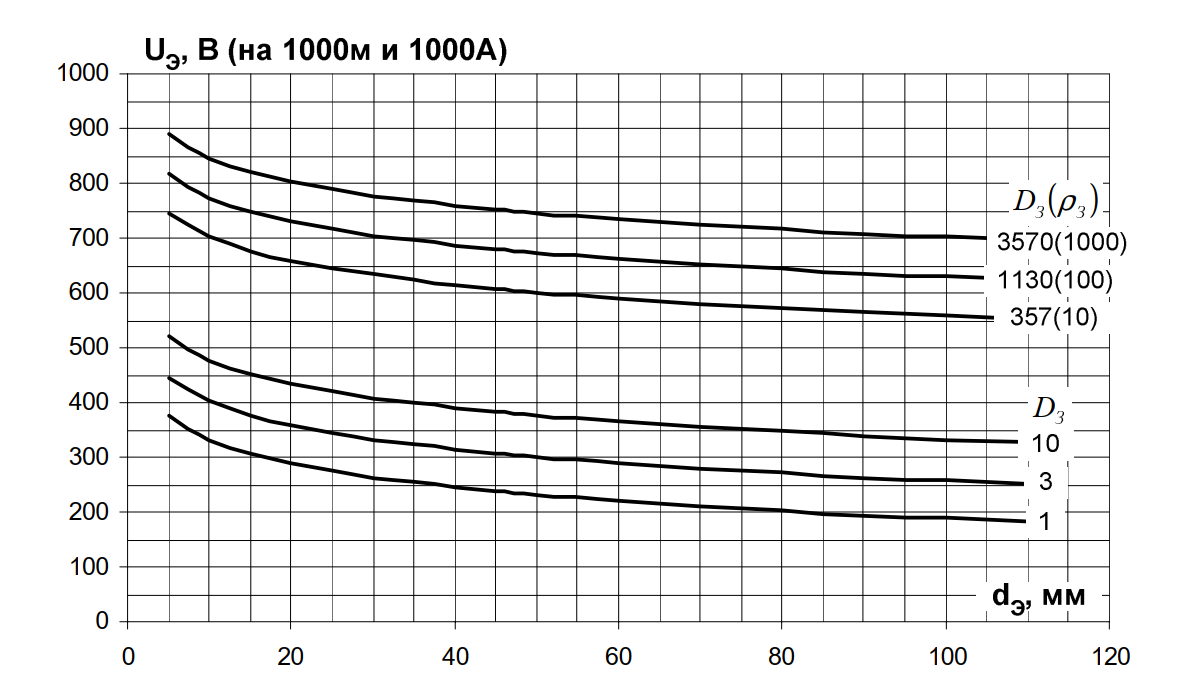
Рис. 3. Напряжение на экране кабеля 6-500 кВ относительно земли, определенное по формуле (3) (режим КЗ) для кабеля длиной 1000 м при токе жилы 1000 А в зависимости от диаметра $ d_{Э} $ и глубины возврата тока через землю $ D_{З} $.
Примечание к рисунку: На оси абсцисс отложен диаметр экрана. Семейство кривых построено для различных значений $ D_{З} $ и удельного сопротивления грунта $ \rho_{З} $.

Для пересчета значений с графиков на реальные параметры линии используется метод пропорций:

U_{Э} = U_{РИС} \cdot \frac{I_{Ж}}{1000} \cdot \frac{L_{К}}{1000}

Если кабель проложен в зоне с развитой системой заземления (территория подстанции, ОРУ), глубина возврата тока $ D_{З} $ мала (1-10 м). В чистом поле она зависит от удельного сопротивления грунта $ \rho_{З} $ (10, 100, 1000 Ом·м).

2.4. Использование транспозиции экранов

Для длинных линий применяется транспозиция экранов (Cross-Bonding) — перекрестная коммутация экранов разных фаз с заземлением в одной точке цикла. Это позволяет векторно суммировать ЭДС трех фаз, что дает в идеале ноль, при этом сохраняя разомкнутый контур для токов промышленной частоты.

Расчетные формулы для различных схем заземления сведены в Таблицу 1.

**Таблица 1.** Напряжение (В), наводимое на экран кабеля относительно земли в различных режимах.
№	Состояние экранов	Симметричный режим работы (нормальный или трехфазное КЗ вне кабеля)	Режим однофазного короткого замыкания вне кабеля
1	Заземлены с одной стороны (K = 1, 2…)	$$ 1 \cdot U_{РИС.2} \cdot \frac{I_{Ж}}{1000} \cdot \frac{L_{К}}{1000} $$	$$ 1 \cdot U_{РИС.3} \cdot \frac{I_{К}}{1000} \cdot \frac{L_{К}}{1000} $$
2	Заземлены с двух сторон	$ \approx 0 $ (Потенциал земли)	$ \approx 0 $ (Потенциал земли)
3	Транспонированы (N = 1, 2…)	$$ \frac{1}{3N} \cdot U_{РИС.2} \cdot \frac{I_{Ж}}{1000} \cdot \frac{L_{К}}{1000} $$ (Остаточное напряжение из-за несимметрии)	$$ \frac{2}{9N} \cdot U_{РИС.2} \cdot \frac{I_{Ж}}{1000} \cdot \frac{L_{К}}{1000} $$ (При КЗ симметрия нарушается)

3. Методика выбора расчетных токов короткого замыкания

3.1. Топология сети и распределение токов

Для корректного использования формул и графиков необходимо правильно определить величину тока $ I_{Ж} $, протекающего непосредственно по жиле кабеля при аварии во внешней сети. Это часто вызывает затруднения у инженеров, так как общий ток КЗ в точке аварии $ I_{K} $ обычно суммируется из нескольких источников и всегда больше или равен току в конкретном кабеле ($ I_{K} \ge I_{Ж} $).

Рассмотрим типовую схему двухцепной кабельной линии между подстанциями ПС-1 и ПС-2 (рис. 4).

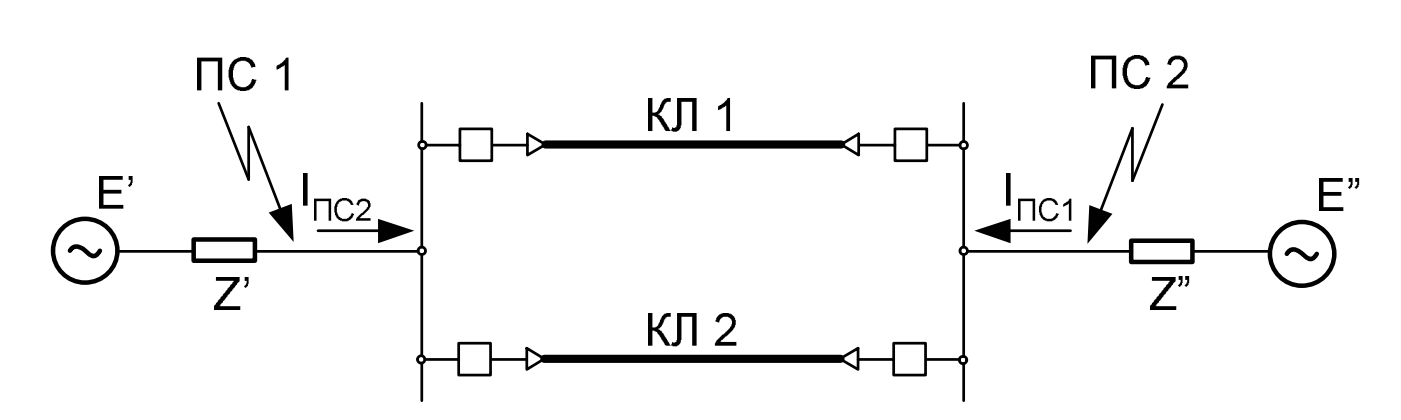
Рис. 4. Схема к вопросу об определении расчетных значений токов короткого замыкания. Показана двухцепная линия, соединяющая два центра питания. Стрелками показаны направления токов подпитки к месту КЗ.

При расчете необходимо рассматривать два сценария:

КЗ на шинах ПС-2: ток подпитки $ I_{Ж1} $ течет от ПС-1 по кабелям.
КЗ на шинах ПС-1: ток подпитки $ I_{Ж2} $ течет от ПС-2 по кабелям.

Величина этих токов зависит от режима работы системы (число включенных цепей $ Q = 1, 2 $) и мощностей короткого замыкания систем, примыкающих к подстанциям. Для расчета применяют метод симметричных составляющих, учитывая сопротивления прямой, обратной и нулевой последовательностей.

3.2. Пример выбора расчетного тока

Предположим, расчеты по методу симметричных составляющих дали следующие значения периодической составляющей суммарного тока в $ Q $ цепях:

Схема (число цепей Q)	КЗ на ПС-2 (ток от ПС-1, $ I_{Ж1} $), кА	КЗ на ПС-1 (ток от ПС-2, $ I_{Ж2} $), кА
Q = 2	17	20
Q = 1	12	15

Алгоритм выбора:

Сравниваем полные токи: $ 20 > 17 $. Худший случай — КЗ на ПС-1.
При двух работающих цепях ($ Q=2 $) суммарный ток 20 кА делится пополам. Ток в одной жиле: $ 20 / 2 = 10 $ кА.
При одной работающей цепи ($ Q=1 $) весь ток течет по одной линии. Ток в жиле: $ 15 $ кА.

Вывод: Для расчета максимального напряжения на экране и выбора ограничителей перенапряжения (ОПН) следует принять расчетный ток $ I_{К(3)} = 15 $ кА. Аналогичный анализ проводится для токов однофазного замыкания $ I_{К(1)} $.

Рекомендация: Если детальные данные о топологии сети и сопротивлениях систем отсутствуют, в целях безопасности (создания запаса прочности) допускается использовать в расчетах полный ток короткого замыкания на шинах подстанции, как если бы он весь протекал через один кабель. Это завысит расчетное напряжение на экране, но гарантирует, что выбранная защита выдержит реальную аварию.

4. Интересные факты об экранах силовых кабелей

Парадокс «нагревателя». При неудачном выборе схемы заземления (например, двухстороннее заземление при плоскостной прокладке) ток в экране может достигать 80-90% от тока в жиле. В этом случае кабель работает как трансформатор с короткозамкнутым витком, превращая дорогую линию электропередачи в гигантский подземный обогреватель грунта.
Геометрия против физики. Простое изменение конфигурации прокладки с «плоскости» (фазы в ряд) на «треугольник» (фазы вплотную вершинами друг к другу) позволяет снизить наводимую ЭДС в экранах в 3-5 раз без применения дорогостоящего оборудования, исключительно за счет взаимной компенсации магнитных полей.
Скрытая угроза КЗ. При коротком замыкании во внешней сети температура медного ленточного экрана может мгновенно подскочить на сотни градусов. Если экран слишком тонок, термическое расширение может деформировать или проплавить внешнюю полиэтиленовую оболочку за доли секунды, нарушив герметичность кабеля еще до срабатывания релейной защиты.
Миф о «нулевом» напряжении. Даже при идеальной реализации цикла транспозиции (Cross-Bonding) напряжение на экранах в узлах коммутации никогда не равно строгому нулю. Из-за неизбежной разницы в длинах секций строительных длин и неоднородности грунта всегда присутствует остаточное напряжение небаланса, которое необходимо контролировать.
Роль грунта как проводника. При расчете напряжений на оболочке критически важно знать удельное сопротивление грунта. В скалистых или сухих песчаных грунтах «глубина возврата тока» через землю может составлять километры, что приводит к кратному росту наводимых перенапряжений по сравнению с влажными глинистыми почвами.
Эволюция материалов. В старых маслонаполненных кабелях свинцовая оболочка выполняла роль и гидроизоляции, и экрана. Современные экраны из медных проволок, скрепленных медной лентой, имеют гораздо меньшее активное сопротивление, что, парадоксальным образом, увеличивает токи потерь при двухстороннем заземлении по сравнению со старыми свинцовыми конструкциями.
Опасность холостого хода. Напряжение на разземленном конце экрана наводится не только от тока нагрузки, но и при включении линии на холостой ход (за счет емкостных токов). Хотя эти токи малы, на длинных сверхвысоковольтных линиях (330-500 кВ) они могут создавать опасный потенциал на экране даже без подключенного потребителя.

5. Часто задаваемые вопросы (FAQ)

1. Почему нельзя просто заземлить экраны с двух сторон на всех линиях и не мучиться с расчетами?

Технически это возможно, но экономически губительно для линий средней и большой длины. При двухстороннем заземлении в экране возникают циркулирующие токи, которые нагревают кабель. Чтобы не перегреть изоляцию, придется снижать допустимый ток нагрузки (пропускную способность линии) на 30–50%. Это означает, что вы покупаете дорогой толстый кабель, но используете его лишь наполовину его возможностей.

2. Зачем нужны ограничители перенапряжения (ОПН) экрана, если экран уже заземлен?

ОПН устанавливаются там, где экран разземлен (при схеме одностороннего заземления или транспозиции). В нормальном режиме ОПН не работает (имеет высокое сопротивление). Однако при ударе молнии или коротком замыкании напряжение на незаземленном конце может подскочить до 5–10 кВ, что пробило бы пластиковую оболочку кабеля. ОПН «срезает» этот опасный импульс, сохраняя целостность оболочки.

3. Какой длины может быть кабельная линия при одностороннем заземлении экранов?

Длина лимитируется величиной наводимого напряжения на незаземленном конце. Согласно ПУЭ, это напряжение не должно превышать 60 В (в некоторых случаях допускается больше при мерах защиты). Обычно для кабелей 10-35 кВ предельная длина составляет 1–2 км, а для кабелей 110 кВ и выше — часто не более 500–800 метров. Если линия длиннее, необходимо применять транспозицию экранов.

4. Можно ли прокладывать однофазные кабели в металлических трубах для защиты?

Категорически запрещено прокладывать отдельный однофазный кабель в стальной магнитной трубе. Труба станет вторичным сердечником, в ней наведутся колоссальные вихревые токи, она раскалится и расплавит изоляцию кабеля. Допускается прокладка всех трех фаз в одной общей стальной трубе (магнитные потоки компенсируются) либо использование немагнитных труб (асбоцементных, пластиковых, из нержавеющей стали).

5. Влияет ли транспозиция экранов на надежность линии?

Транспозиция усложняет линию, добавляя «слабые звенья» — коробки транспозиции и коаксиальные кабели вывода экранов. Статистика показывает, что проблемы часто возникают именно в узлах коммутации (попадание влаги в коробки, выход из строя ОПН). Поэтому применение транспозиции оправдано только там, где двухстороннее заземление недопустимо по потерям, а одностороннее невозможно по длине.

Заключение

Проектирование кабельных линий высокого напряжения требует тщательного анализа электромагнитных процессов. Правильный расчет индуктированных токов и напряжений позволяет:

Оптимизировать сечение экранов, избегая перерасхода цветных металлов.
Выбрать оптимальную схему заземления (двухстороннее, одностороннее или транспозиция), балансируя между потерями мощности и сложностью монтажа.
Обеспечить безопасность эксплуатационного персонала в соответствии с ГОСТ 12.1.038.
Правильно выбрать параметры ОПН для защиты оболочки кабеля от пробоя при внешних КЗ.

Приведенные в статье методики и графические зависимости являются удобным инструментом для быстрой инженерной оценки параметров на стадии предпроектной проработки и технико-экономического обоснования (ТЭО).

Нормативная база

СТО 56947004-29.060.20.072-2010. Методические указания по выбору способа заземления экранов, ограничителей перенапряжений и изоляции оболочки силовых кабелей с изоляцией из сшитого полиэтилена на напряжение 6-500 кВ. — Введ. 2010-06-25. — М.: ОАО «ФСК ЕЭС», 2010.
ПУЭ (Правила устройства электроустановок). 7-е издание. Глава 2.3 «Кабельные линии напряжением до 220 кВ».
ГОСТ Р 55025-2012. Кабели силовые с пластмассовой изоляцией на номинальное напряжение от 6 до 35 кВ включительно. Общие технические условия.

Список литературы

Дмитриев М.В. Заземление экранов однофазных силовых кабелей 6-500 кВ. — СПб.: Изд-во Политехн. ун-та, 2010. — 152 с.
Ларина Э.Т. Силовые кабели и высоковольтные кабельные линии: Учебник для вузов. — М.: Энергоатомиздат, 1996. — 464 с.
Крючков И.П., Старшинов В.А., Пираторов М.В. Переходные процессы в электроэнергетических системах. — М.: Энергоатомиздат, 2008.

Расчет индуктированных токов и напряжений в экранах однофазных силовых кабелей: методика, физика процессов