Вращающееся магнитное поле: получение, теория, применение

Содержание страницы

1. Поле однофазной катушки (Пульсирующее поле)
2. Получение поля в трехфазной системе
3. Получение поля в двухфазной системе
4. Применение в электрических двигателях
5. Сравнительная таблица асинхронных и синхронных двигателей
6. Интересные факты о вращающемся поле
7. Часто задаваемые вопросы (FAQ)
Заключение

Вращающееся магнитное поле — это магнитное поле, вектор индукции которого изменяет свое направление в пространстве с течением времени, как бы «поворачиваясь» вокруг некоторой оси. В контексте электротехники, этот термин чаще всего описывает поле постоянной величины (амплитуды), которое вращается с постоянной угловой скоростью (синхронной скоростью). Это явление является фундаментальным принципом, лежащим в основе работы большинства электрических машин переменного тока.

Исторически, концепция была независимо разработана двумя выдающимися инженерами в 1880-х годах: Галилео Феррарисом в Италии и Николой Теслой в США. Демонстрация Теслой асинхронного двигателя, работающего на этом принципе, в 1888 году стала решающим фактором в «Войне токов», обеспечив победу систем переменного тока (AC) над системами постоянного тока (DC) для генерации и распределения электроэнергии.

1. Поле однофазной катушки (Пульсирующее поле)

Если по одиночной катушке протекает синусоидальный ток $i(t) = I_m \sin(\omega t)$, она создает магнитодвижущую силу (МДС) и, соответственно, магнитное поле, которое также изменяется синусоидально. Однако это поле является пульсирующим, а не вращающимся. Его вектор направлен вдоль оси катушки и лишь меняет свою величину и полярность.

Математически, используя формулу Эйлера, такое пульсирующее поле $B(t)$ можно представить как сумму двух магнитных полей, вращающихся в противоположные стороны с одинаковой угловой скоростью $\omega$:

$$ B(t) = B_m \sin(\omega t) = B_m \frac{e^{j\omega t} — e^{-j\omega t}}{2j} $$

Здесь $ \frac{B_m}{2j}e^{j\omega t} $ представляет поле, вращающееся в одном (прямом) направлении, а $ -\frac{B_m}{2j}e^{-j\omega t} $ — поле, вращающееся в обратном направлении. Для запуска двигателя такое поле неэффективно, так как пусковые моменты от этих двух полей компенсируют друг друга.

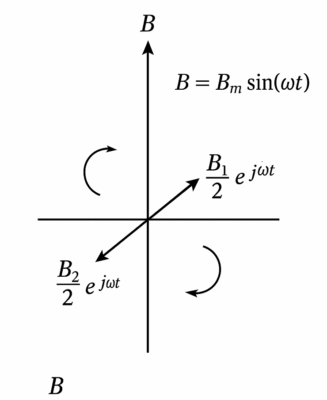
Диаграмма, показывающая пульсирующее магнитное поле (вертикальная ось) как сумму двух контр-вращающихся векторов (прямого и обратного)

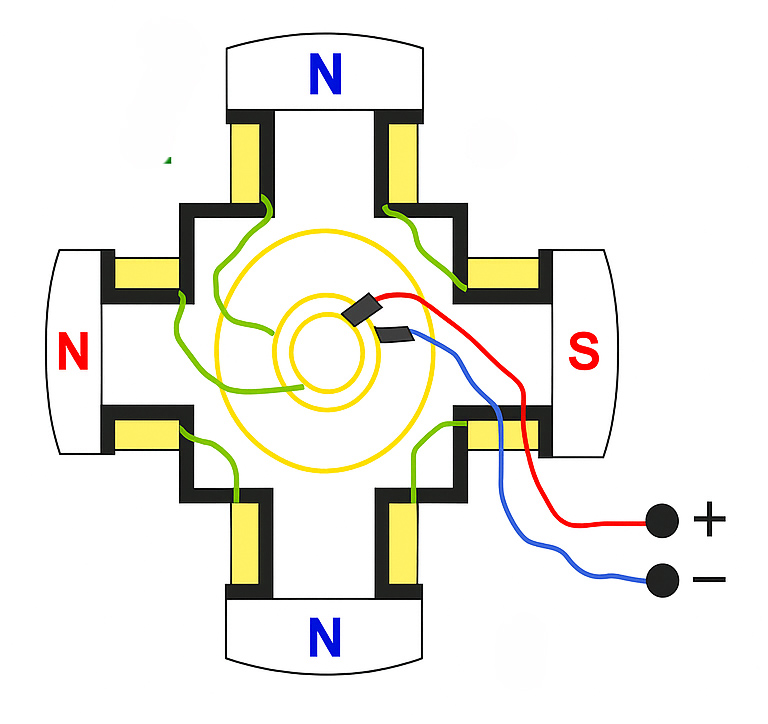
Рисунок 1 — Представление пульсирующего поля в виде суммы двух вращающихся полей.

2. Получение поля в трехфазной системе

Для получения истинно вращающегося (кругового) поля постоянной амплитуды необходима многофазная система. Стандартом де-факто является трехфазная система.

Конструктивно в статоре (неподвижной части машины) размещают три одинаковые обмотки (A, B, C), оси которых сдвинуты в пространстве друг относительно друга на угол 120° (или $2\pi/3$ радиан). Эти обмотки подключаются к симметричной трехфазной системе ЭДС, где напряжения (и токи) сдвинуты по фазе также на 120°.

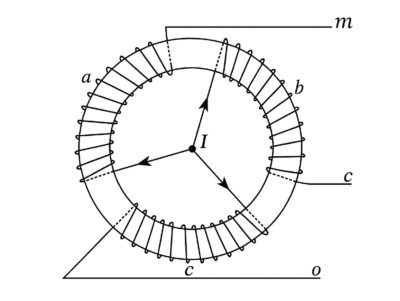
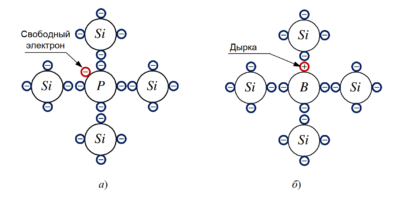
Рисунок 2 — Пространственное расположение трехфазных обмоток статора.

Пусть МДС каждой фазы равны:

Фаза A (ось 0°): $ F_A(t) = F_m \sin(\omega t) $
Фаза B (ось 120°): $ F_B(t) = F_m \sin(\omega t — 120^\circ) $
Фаза C (ось 240°): $ F_C(t) = F_m \sin(\omega t — 240^\circ) $

Результирующее поле $\vec{F}_{res}$ является векторной суммой полей трех фаз. Для строгого математического доказательства удобно использовать комплексное представление. Каждое пульсирующее поле (как в разделе 1) раскладывается на два вращающихся. Результирующее поле будет суммой шести компонентов (три «прямых» и три «обратных»).

Сумма прямых полей (с учетом их пространственного сдвига $a = e^{j120^\circ}$ и $a^2 = e^{j240^\circ}$):

$$ \vec{F}_{прям} = \frac{F_m}{2j} [e^{j\omega t} + a \cdot e^{j(\omega t — 120^\circ)} + a^2 \cdot e^{j(\omega t — 240^\circ)}] $$

Так как $ e^{-j120^\circ} = a^2 $ и $ e^{-j240^\circ} = a $, получаем:

$$ \vec{F}_{прям} = \frac{F_m}{2j} [e^{j\omega t} + (a \cdot a^2) e^{j\omega t} + (a^2 \cdot a) e^{j\omega t}] = \frac{F_m}{2j} [e^{j\omega t} + e^{j\omega t} + e^{j\omega t}] = \frac{3 F_m}{2j} e^{j\omega t} $$

Сумма обратных полей:

$$ \vec{F}_{обр} = -\frac{F_m}{2j} [e^{-j\omega t} + a \cdot e^{-j(\omega t — 120^\circ)} + a^2 \cdot e^{-j(\omega t — 240^\circ)}] $$
$$ \vec{F}_{обр} = -\frac{F_m}{2j} e^{-j\omega t} [1 + a \cdot e^{j120^\circ} + a^2 \cdot e^{j240^\circ}] = -\frac{F_m}{2j} e^{-j\omega t} [1 + a^2 + a^4] $$

Поскольку $a^4 = a$, выражение в скобках становится $(1 + a + a^2)$, что является суммой векторов сбалансированной трехфазной системы и тождественно равно нулю.

Таким образом, результирующее поле $\vec{F}_{res} = \vec{F}_{прям}$ имеет постоянную амплитуду $1.5 F_m$ и вращается с угловой скоростью $\omega$, равной угловой частоте питающей сети. Эта скорость называется синхронной скоростью.

3. Получение поля в двухфазной системе

Аналогично можно доказать, что вращающееся магнитное поле также образуют две катушки, оси которых повернуты в пространстве на 90° друг относительно друга, а токи в них сдвинуты по фазе на 90°. Этот принцип используется, например, в однофазных асинхронных двигателях, где вторая «фаза» создается искусственно с помощью конденсатора или пусковой обмотки.

4. Применение в электрических двигателях

Это явление является основой для создания асинхронных и синхронных электродвигателей. У этих двигателей имеется неподвижный статор, в пазах которого и располагаются обмотки, создающие вращающееся магнитное поле. Внутри статора находится подвижная часть — ротор, который выполняется по-разному для этих типов двигателей.

4.1. Асинхронный (индукционный) двигатель

Ротор асинхронного двигателя выполняется в виде «беличьей клетки» (короткозамкнутый ротор) или в виде нескольких обмоток, замкнутых на себе или на внешнее сопротивление (фазный ротор). «Беличья клетка» представляет собой массивные проводящие стержни (обычно алюминиевые), соединенные по торцам замыкающими кольцами.

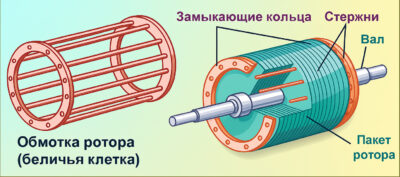
Рисунок 3 — Конструкция короткозамкнутого ротора («беличья клетка»).

Ротор этого двигателя вращается медленнее, чем вращающееся магнитное поле, то есть асинхронно. Разница в скоростях необходима для работы.

Принцип действия (Асинхронный режим)

Рассмотрим процессы, происходящие при работе. Когда ротор неподвижен (в момент пуска), вращающееся магнитное поле статора пересекает проводники или стержни ротора с максимальной относительной скоростью. Это наводит в них ЭДС (ЭлектроДвижущую Силу) по закону электромагнитной индукции. Для отдельного проводника эта ЭДС определяется уравнением:

$$ E = Blv $$

где:

$B$ — магнитная индукция поля;
$l$ — активная длина проводника в поле;
$v$ — относительная скорость движения поля относительно проводника.

Поскольку обмотка ротора замкнута, под действием этой ЭДС по проводникам ротора протекает ток $I$. Взаимодействие этого тока с магнитным полем статора создает силу Ампера (силу Лоренца), которая для отдельного проводника определяется уравнением:

$$ F = IBl $$

Сумма этих сил для всех проводников ротора создает вращающий момент, под действием которого ротор приходит во вращение в ту же сторону, что и поле статора.

Концепция скольжения (Slip)

Ротор асинхронного двигателя никогда не может достичь скорости вращения магнитного поля (синхронной скорости). Если бы это произошло, то относительная скорость $v$ проводников ротора и магнитного поля стала бы равной нулю. В этом случае:

Стала бы равной нулю ЭДС $E$ ($E = Bl \cdot 0 = 0$).
Прекратился бы ток в роторе $I$.
Исчезла бы сила $F$ ($F = 0 \cdot Bl = 0$) и, следовательно, вращающий момент.

Поэтому для создания момента ротор всегда должен «отставать» от поля. Эта разница в скоростях называется скольжением (s) и является ключевой характеристикой асинхронной машины.

4.2. Синхронный двигатель

У синхронного двигателя ротор выполняют в виде постоянного магнита или электромагнита, питаемого постоянным током (через щеточный узел или бесщеточную систему возбуждения). Полюсы этого ротора «сцепляются» с вращающимся полем статора и увлекаются им.

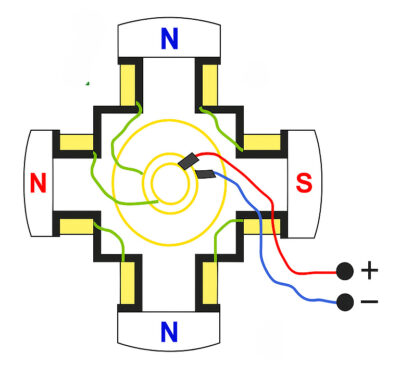
Рисунок 4 — Конструкция ротора синхронного двигателя с обмоткой возбуждения.

Поэтому ротор синхронного двигателя вращается вслед за вращающимся магнитным полем, то есть синхронно — с той же скоростью, что и поле статора, независимо от нагрузки (в пределах допустимого момента).

Преимущества и недостатки двигателей

Асинхронные двигатели:

Преимущества: Исключительная простота конструкции (особенно с «беличьей клеткой»), высокая надежность, низкая стоимость, простота в эксплуатации.
Недостатки: Сложность регулирования частоты вращения (без частотного преобразователя), потребление реактивной мощности, меньший КПД по сравнению с синхронными (особенно при неполной нагрузке).

Синхронные двигатели:

Преимущества: Строго постоянная частота вращения, не зависящая от нагрузки; высокий КПД; возможность работы с опережающим коэффициентом мощности (генерация реактивной мощности в сеть для компенсации).
Недостатки: Сложность конструкции (необходимость источника питания ротора), более высокая стоимость, необходимость пускового устройства (сами по себе не имеют пускового момента).

5. Сравнительная таблица асинхронных и синхронных двигателей

Характеристика	Асинхронный двигатель	Синхронный двигатель
Принцип создания момента	Индукционный (токи наводятся в роторе)	Реактивный (взаимодействие полей статора и ротора)
Конструкция ротора	«Беличья клетка» (КЗ) или фазный (обмотки)	Постоянные магниты или электромагнит (обмотка возбуждения)
Частота вращения ротора	Асинхронная (всегда меньше синхронной, зависит от нагрузки)	Синхронная (строго равна скорости поля, не зависит от нагрузки)
Пусковой момент	Присутствует (зависит от конструкции)	Нулевой (требует пусковой обмотки или частотного пуска)
Коэффициент мощности ($\cos \varphi$)	Всегда отстающий (потребляет реактивную мощность)	Может регулироваться (отстающий, единичный, опережающий)
Применение	Насосы, вентиляторы, конвейеры, станки (самый массовый тип)	Компрессоры, мельницы (мощные нагрузки), генераторы, компенсаторы

6. Интересные факты о вращающемся поле

Победа в «Войне токов»: Именно патент Николы Теслы на асинхронный двигатель, использующий вращающееся поле, стал главным козырем Джорджа Вестингауза в борьбе против систем постоянного тока Томаса Эдисона.
Линейный двигатель: Если «развернуть» статор с его обмотками в плоскость, вращающееся поле превратится в «бегущее» поле. Это принцип работы линейных асинхронных двигателей, которые используются в поездах на магнитной подушке (Маглев).
Скольжение — это не дефект: Отставание ротора (скольжение) в асинхронном двигателе не является недостатком. Это необходимое физическое условие для индукции тока в роторе и, следовательно, для создания вращающего момента.
Управление скоростью: Десятилетиями асинхронные двигатели были нерегулируемыми. Революцию в промышленности произвело изобретение полупроводниковых преобразователей частоты (ПЧ), которые позволяют легко менять скорость вращающегося поля и, как следствие, скорость ротора.
Обратимость машины: Любая вращающаяся электрическая машина обратима. Если асинхронный двигатель раскрутить внешним моментом (например, ветром) быстрее синхронной скорости, он перейдет в генераторный режим и начнет отдавать энергию в сеть.
Компенсация реактивной мощности: Крупные синхронные двигатели на промышленных предприятиях часто запускают в режиме «синхронного компенсатора» (без механической нагрузки), чтобы они генерировали реактивную мощность и улучшали общий коэффициент мощности сети предприятия.
Теорема Леблана: Математическое разложение пульсирующего поля на два вращающихся в разные стороны (упомянутое в разделе 1) носит название теоремы Леблана.

7. Часто задаваемые вопросы (FAQ)

1. Что такое вращающееся магнитное поле?

Это магнитное поле, вектор индукции которого не пульсирует на месте, а вращается в пространстве с постоянной скоростью (синхронной скоростью) и имеет неизменную амплитуду. Оно создается многофазными (обычно тремя) обмотками, сдвинутыми в пространстве и питаемыми токами, сдвинутыми по фазе.

2. Почему поле от трех фаз вращается, а от одной — нет?

Одна фаза создает пульсирующее поле, которое можно представить как сумму двух полей, вращающихся навстречу друг другу (их моменты компенсируются). В трехфазной системе «обратные» компоненты полей взаимно уничтожаются, а «прямые» — складываются, образуя одно результирующее поле постоянной величины, вращающееся в одном направлении.

3. В чем разница между синхронной и асинхронной скоростью?

Синхронная скорость — это скорость вращения магнитного поля статора, она жестко задается частотой сети ($n_{sync} = 60 \cdot f / p$, где $f$ — частота, $p$ — число пар полюсов). Асинхронная скорость — это фактическая скорость вращения ротора асинхронного двигателя. Она всегда немного меньше синхронной.

4. Что такое «скольжение» (slip) в асинхронном двигателе?

Скольжение — это относительная разница между синхронной скоростью поля ($n_1$) и асинхронной скоростью ротора ($n_2$), выраженная в процентах или долях единицы. Формула: $s = (n_1 — n_2) / n_1$. Скольжение необходимо для создания крутящего момента. При $\approx 0\%$ (холостой ход) момент почти нулевой, при $\approx 100\%$ (заторможенный ротор) — пусковой момент.

5. Может ли однофазный двигатель создать вращающееся поле?

Не самостоятельно. Однофазная обмотка создает только пульсирующее поле (нулевой пусковой момент). Для запуска в однофазных двигателях используют вспомогательную пусковую обмотку, фаза тока в которой сдвигается (обычно на 90°) с помощью конденсатора. Это создает эллиптическое (неидеальное, но вращающееся) поле, достаточное для пуска.

6. Что произойдет, если ротор асинхронного двигателя раскрутить до синхронной скорости?

Вращающий момент станет равен нулю. Относительная скорость между полем и ротором будет 0, ЭДС в роторе не будет наводиться, ток в роторе исчезнет. Двигатель перейдет в режим идеального холостого хода (что на практике недостижимо из-за трения).

7. Зачем нужен синхронный двигатель, если он сложнее?

Он незаменим там, где требуется строго постоянная скорость вращения независимо от нагрузки (например, в точных механизмах, генераторах). Кроме того, в мощных установках (от сотен кВт) его высокий КПД и способность регулировать коэффициент мощности (улучшать качество электроэнергии в сети) экономически оправдывают его сложность.

Заключение

Принцип получения вращающегося магнитного поля является одним из величайших достижений в истории электротехники. Эта концепция, основанная на использовании многофазных систем переменного тока, позволила создать простые, надежные и эффективные электродвигатели, которые привели в движение промышленную революцию и продолжают оставаться «рабочими лошадками» современной цивилизации. Понимание этого фундаментального процесса является обязательным для любого инженера-электрика, так как на нем базируется работа абсолютного большинства генераторов и двигателей переменного тока.

Нормативные документы

Технические требования, методы испытаний и параметры вращающихся электрических машин в России и странах СНГ регламентируются межгосударственными стандартами (ГОСТ). Актуальные стандарты включают:

ГОСТ IEC 60034-1-2024 — Машины электрические вращающиеся. Часть 1. Номинальные значения параметров и эксплуатационные характеристики. (Самый современный общий стандарт).
ГОСТ 31606-2012 — Машины электрические вращающиеся. Двигатели асинхронные мощностью от 0,12 до 400 кВт включительно. Общие технические требования.
ГОСТ 11828-86 — Машины электрические вращающиеся. Общие методы испытаний.
ГОСТ 16264.2-2018 — Двигатели синхронные. Общие технические условия. (Для машин малой мощности).

Получение вращающегося магнитного поля в электрических машинах