Периодические несинусоидальные токи в трехфазных цепях

Содержание страницы

Разложение несинусоидальных сигналов в ряд Фурье
Последовательности гармоник в трехфазных системах
Особенности гармоник, кратных трем (нулевой последовательности)
Влияние на линии связи
Сравнение последовательностей гармоник
Примеры расчета
Интересные факты о гармониках
FAQ: Часто задаваемые вопросы
Заключение

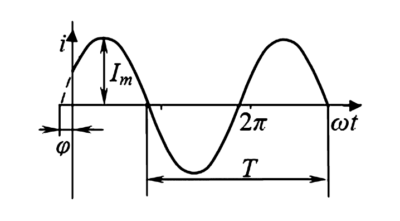
Периодический несинусоидальный ток (или напряжение) — это любой периодический сигнал в электрической цепи, форма которого отличается от идеальной синусоиды. Такие сигналы характерны для современных систем электроснабжения из-за широкого распространения нелинейных нагрузок, таких как выпрямители, преобразователи частоты, импульсные источники питания и люминесцентные лампы.

Исторически, основы анализа таких сложных сигналов были заложены в начале 19-го века французским математиком Жаном-Батистом Жозефом Фурье. Он доказал, что любую периодическую функцию можно представить в виде суммы синусоидальных колебаний с различными частотами, амплитудами и фазами (то есть в виде ряда Фурье). В электротехнике это открытие позволило применять для расчета сложных цепей методы, разработанные для синусоидального тока, к каждой гармонике отдельно, с последующим суммированием результатов.

Разложение несинусоидальных сигналов в ряд Фурье

При анализе несинусоидальных токов и напряжений их раскладывают в ряд Фурье. В этом разложении различают три основных компоненты:

Постоянная составляющая ( $I_0$ ) — гармоника нулевой частоты, или среднее значение тока за период.
Основная (первая) гармоника ( $i_1$ ) — синусоидальная составляющая, частота которой равна частоте несинусоидального сигнала (обычно 50 или 60 Гц).
Высшие гармоники ( $i_n, n > 1$ ) — все остальные синусоидальные составляющие, частоты которых в $n$ раз превышают частоту основной гармоники.

Рассмотрим особенности расчетов симметричных трехфазных цепей, обусловленные наличием высших гармоник. В таких цепях токи и напряжения в любой из фаз (A, B, C) смещены относительно друг друга на 1/3 периода основной гармоники (то есть на $120^\circ$ или $2\pi/3$ радиан).

Однако 1/3 периода основной гармоники равна целому периоду третьей гармоники ( $3 \times 120^\circ = 360^\circ$ ). По этой причине третьи гармоники во всех фазах симметричных трехфазных цепей оказываются синфазными (совпадающими по фазе). Это же справедливо и для всех гармоник, кратных трем (6-й, 9-й, 12-й и т.д.), а также для постоянной составляющей.

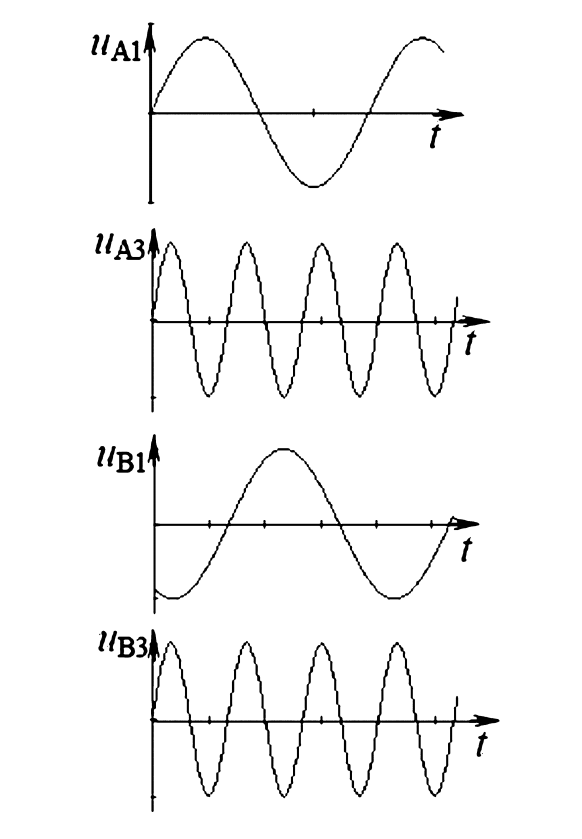
Рис. 1. Сопоставление первой (a) и третьей (б) гармоник в фазах A и B. Видно, что первые гармоники сдвинуты на 120°, в то время как третьи гармоники совпадают по фазе.

Последовательности гармоник в трехфазных системах

Для $n$-ой гармоники в симметричной системе фазные напряжения (или токи) могут быть описаны относительно фазы A:

Напряжение фазы A: $ \dot{U}_{An} $
Напряжение фазы B: $ \dot{U}_{Bn} = \dot{U}_{An} \cdot e^{-j n 2\pi/3} $
Напряжение фазы C: $ \dot{U}_{Cn} = \dot{U}_{An} \cdot e^{+j n 2\pi/3} $

В зависимости от номера гармоники $n$, результирующая система векторов образует три различные последовательности:

Прямая последовательность (n = 1, 4, 7, …):
При $n=1$, сдвиг фаз составляет $-120^\circ$ и $+120^\circ$. Это стандартная последовательность (A-B-C), совпадающая с чередованием фаз основной гармоники.
Обратная последовательность (n = 2, 5, 8, …):
При $n=2$, фазовый сдвиг для фазы B становится $ -2 \cdot 120^\circ = -240^\circ $, что эквивалентно $+120^\circ$. Для фазы C сдвиг равен $+240^\circ$, что эквивалентно $-120^\circ$. Последовательность чередования фаз меняется на обратную (A-C-B).
Нулевая последовательность (n = 3, 6, 9, …):
При $n=3$, сдвиг для фазы B равен $ -3 \cdot 120^\circ = -360^\circ $, что эквивалентно $0^\circ$. Для фазы C сдвиг $+360^\circ$, что также эквивалентно $0^\circ$. Все три вектора гармоник, кратных трем, совпадают по фазе (синфазны): $ \dot{U}_{A3} = \dot{U}_{B3} = \dot{U}_{C3} $.

Особенности гармоник, кратных трем (нулевой последовательности)

Гармоники, кратные трем, из-за своего синфазного характера создают ряд специфических проблем в симметричных трехфазных системах:

Отсутствие в линейных напряжениях. Линейное напряжение, например, $ u_{AB} = u_A — u_B $. Так как для 3-й (и кратных ей) гармоник $ u_{A3}(t) = u_{B3}(t) $, их разность всегда равна нулю.
- Преимущество: Нагрузки, подключенные «в треугольник» или между линиями (например, асинхронные двигатели), не подвержены прямому влиянию этих гармоник.
- Недостаток: Эти гармоники «невидимы» для приборов, измеряющих линейное напряжение, что может маскировать проблемы в цепи.
Суммирование в нулевом (нейтральном) проводе. Ток в нейтральном проводе равен сумме фазных токов: $ i_N = i_A + i_B + i_C $. Для гармоник, кратных трем, $ i_{N3} = i_{A3} + i_{B3} + i_{C3} = 3 \cdot i_{A3} $.
- Недостаток: Это приводит к утроенному току в нейтрали. В системах с большим количеством однофазных нелинейных нагрузок (например, офисные здания с компьютерами) ток в нейтрали может превысить фазный, вызывая ее перегрев и пожароопасную ситуацию, если она не рассчитана на такую нагрузку.
Смещение нейтрали при отсутствии нулевого провода. В четырехпроводной системе (схема «звезда с нулем») ток 3-й гармоники замыкается через нулевой провод. Если этот провод отсутствует (схема «звезда без нуля»), ток протекать не может. В результате напряжение между нейтральными точками генератора (N) и нагрузки (n) определяется только этими гармониками, что приводит к искажению фазных напряжений нагрузки.
Циркулирующие токи в «треугольнике». Если фазные ЭДС генератора содержат гармоники, кратные трем, то при соединении обмоток в «треугольник» эти ЭДС суммируются в контуре: $ \dot{E}_{контура} = \dot{E}_{A3} + \dot{E}_{B3} + \dot{E}_{C3} = 3 \cdot \dot{E}_{A3} $. Эта ЭДС создает значительный циркулирующий ток 3-й гармоники внутри обмоток, даже при отсутствии внешней нагрузки, вызывая дополнительный нагрев.

Влияние на линии связи

Трехфазные линии электропередачи с заземленными нейтралями могут оказывать сильное мешающее влияние на параллельные линии связи. Это связано именно с наличием гармоник, кратных трем. Токи этих (нулевой последовательности) синусоидальных составляющих протекают по широкой петле (провода — земля — провода), создавая сильное магнитное поле. Это поле, имеющее к тому же повышенную частоту (150 Гц, 250 Гц, 450 Гц и т.д.), близкую к частотам спектра разговорной речи, наводит помехи в линиях связи.

Примечание: Регулирование качества электроэнергии

В Российской Федерации качество электрической энергии, включая уровни гармонических составляющих напряжения, нормируется межгосударственным стандартом ГОСТ 32144-2013 «Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения».

Этот стандарт, гармонизированный с европейским EN 50160, устанавливает предельно допустимые значения для коэффициента $n$-ой гармонической составляющей напряжения в точке передачи электроэнергии. Соблюдение этих норм критически важно для обеспечения электромагнитной совместимости (ЭМС) оборудования и предотвращения негативного влияния гармоник на сети.

Сравнение последовательностей гармоник

Характеристика	Прямая последовательность	Обратная последовательность	Нулевая последовательность
Номера гармоник (n)	1, 4, 7, 10, …	2, 5, 8, 11, …	3, 6, 9, 12, …
Чередование фаз	A-B-C (Прямое)	A-C-B (Обратное)	A, B, C (Синфазны)
Сумма векторов в нейтрали $ (\dot{I}_A + \dot{I}_B + \dot{I}_C) $	$ \approx 0 $ (в симметричной системе)	$ \approx 0 $ (в симметричной системе)	$ 3 \cdot \dot{I}_A $ (Не равна нулю!)
Наличие в линейном напряжении $ (U_{AB}) $	Да	Да	Нет
Основное влияние	Основной рабочий поток мощности.	Создает тормозной момент в двигателях, вызывает вибрации.	Перегрев нейтрали, помехи связи, искажение фазных напряжений.

Примеры расчета

Пример 1

Известно, что в фазном напряжении обмоток трансформатора содержатся первая и третья гармонические составляющие. Система симметрична. При соединении обмоток в «звезду» измерены фазное напряжение $ U_Ф = 131 $ кВ и линейное напряжение $ U_Л = 220 $ кВ. Чему равно фазное напряжение третьей гармоники?

Решение:

В линейном напряжении третья гармоника отсутствует, поэтому измеренное линейное напряжение 220 кВ создается только первой гармоникой. Связь между линейным и фазным напряжением для первой (прямой) последовательности:

$$ U_{Л1} = U_{Ф1} \cdot \sqrt{3} $$

Отсюда находим действующее значение фазного напряжения первой гармоники:

$$ U_{Ф1} = \frac{U_{Л1}}{\sqrt{3}} = \frac{220 \text{ кВ}}{\sqrt{3}} \approx 127 \text{ кВ} $$

Фазное напряжение $ U_Ф $ является действующим значением несинусоидального сигнала и равно корню из суммы квадратов действующих значений всех его гармоник:

$$ U_Ф = \sqrt{U_{Ф1}^2 + U_{Ф3}^2} $$

Возводя обе части в квадрат, выражаем напряжение третьей гармоники:

$$ U_{Ф3}^2 = U_Ф^2 — U_{Ф1}^2 $$
$$ U_{Ф3} = \sqrt{U_Ф^2 — U_{Ф1}^2} = \sqrt{131^2 — 127^2} = \sqrt{17161 — 16129} = \sqrt{1032} \approx 32.12 \text{ кВ} $$

Ответ: Фазное напряжение третьей гармоники составляет $ \approx 32.12 $ кВ.

Пример 2

Для схемы, показанной на рис. 2, ЭДС фазы A равна:
$ e_A(t) = 170\sin(\omega t) + 80\cos(3\omega t) + 34\cos(9\omega t) $ В.
Параметры цепи: $ R = 9 $ Ом, $ \omega L = 2 $ Ом, $ \omega = 314 $ с⁻¹.
Схема симметричная, четырехпроводная, но нулевой провод отсутствует.

Определить показания всех приборов (A, V1, V2, V3, V4, V5). Приборы электродинамической системы (измеряют действующие значения).

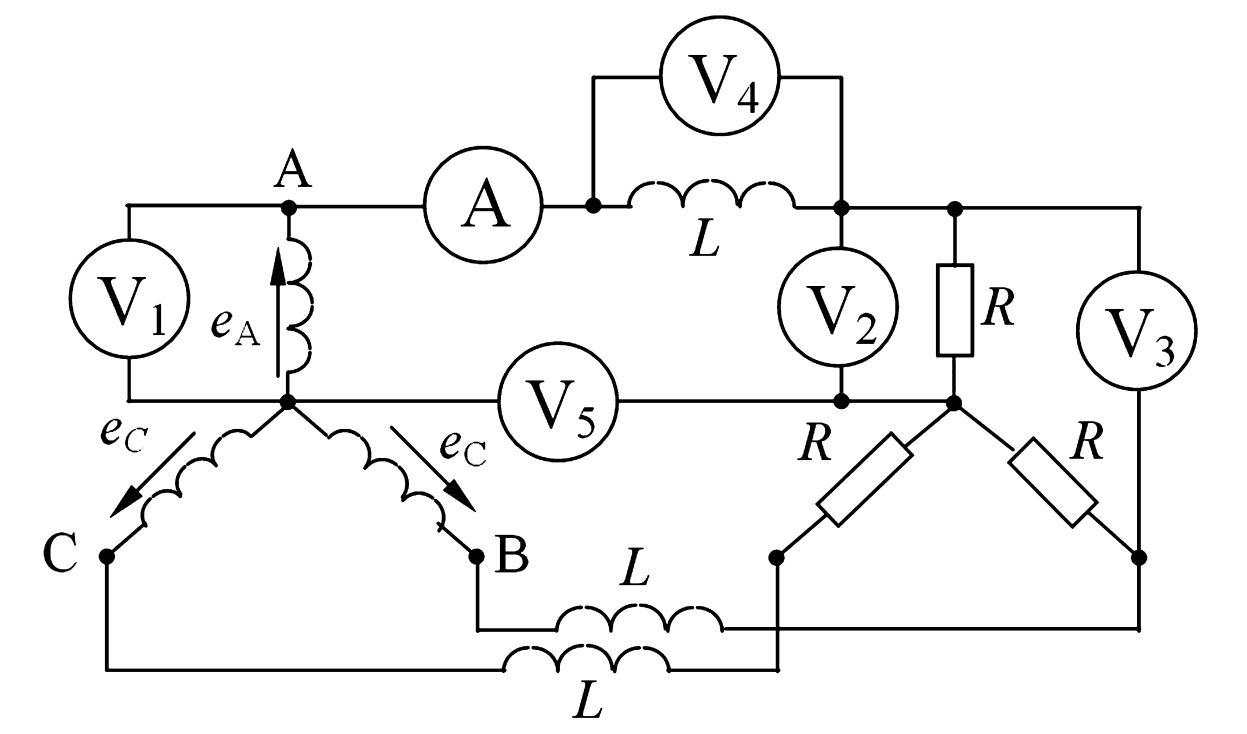
Рис. 2. Схема к примеру 2

Решение:

1. Определяем действующие значения ЭДС по гармоникам:

$ E_1 = \frac{170}{\sqrt{2}} \approx 121 \text{ В} $
$ E_3 = \frac{80}{\sqrt{2}} \approx 56.5 \text{ В} $
$ E_9 = \frac{34}{\sqrt{2}} \approx 24.2 \text{ В} $

2. Из-за отсутствия нулевого провода, токи гармоник, кратных трем (нулевой последовательности), протекать не могут. Поэтому в линейных проводах (и, следовательно, через амперметр A, R и L) будет протекать только первая гармоника тока.

Полное сопротивление фазы для первой гармоники:

$$ Z_1 = \sqrt{R^2 + (\omega L)^2} = \sqrt{9^2 + 2^2} = \sqrt{81 + 4} = \sqrt{85} \approx 9.22 \text{ Ом} $$

3. Показание амперметра A (ток первой гармоники):

$$ I_A = I_1 = \frac{E_1}{Z_1} = \frac{121 \text{ В}}{9.22 \text{ Ом}} \approx 13.12 \text{ А} $$

(Примечание: в исходном тексте было 13.2А, что привело бы к $ E_1 = 13.2 \cdot 9.22 \approx 121.7 \text{ В} $. Используем более точное значение 13.12 А для согласованности расчетов.)

4. Показание вольтметра V1 (фазное напряжение генератора):

V1 измеряет полное действующее значение ЭДС, т.к. ток по фазе не течет (кроме I1, но V1 измеряет ЭДС источника):

$$ V_1 = E_{Ф} = \sqrt{E_1^2 + E_3^2 + E_9^2} = \sqrt{121^2 + 56.5^2 + 24.2^2} = \sqrt{14641 + 3192.25 + 585.64} \approx 135.7 \text{ В} $$

5. Показание вольтметра V2 (фазное напряжение на резисторе R нагрузки):

На нагрузке протекает только ток $ I_1 $. Напряжение на резисторе создается только этим током.

$$ V_2 = U_{R} = I_1 \cdot R = 13.12 \text{ А} \cdot 9 \text{ Ом} \approx 118.08 \text{ В} $$

6. Показание вольтметра V3 (линейное напряжение на нагрузке):

На нагрузке присутствуют только гармоники прямой последовательности (первая). Гармоники, кратные трем, отсутствуют.

$$ V_3 = U_{Л.нагр} = U_{Ф.нагр} \cdot \sqrt{3} = V_2 \cdot \sqrt{3} = 118.08 \text{ В} \cdot \sqrt{3} \approx 204.5 \text{ В} $$

7. Показание вольтметра V4 (напряжение на индуктивности L):

На индуктивности, как и на резисторе, падение напряжения создает только ток $ I_1 $.

$$ V_4 = U_L = I_1 \cdot (\omega L) = 13.12 \text{ А} \cdot 2 \text{ Ом} = 26.24 \text{ В} $$

8. Показание вольтметра V5 (напряжение смещения нейтрали $ U_{Nn} $):

Это напряжение между нейтралью генератора (N) и нейтралью нагрузки (n). Оно определяется суммой ЭДС тех гармоник, которые не могут создать ток в цепи, т.е. гармоник нулевой последовательности (3-й и 9-й).

$$ V_5 = U_{Nn} = \sqrt{E_3^2 + E_9^2} = \sqrt{56.5^2 + 24.2^2} = \sqrt{3192.25 + 585.64} \approx 61.46 \text{ В} $$

Интересные факты о гармониках

«Поющие» трансформаторы: Низкочастотный гул, который издают силовые трансформаторы, не всегда связан только с основной частотой 50/60 Гц. Высшие гармоники тока вызывают магнитные поля на кратных частотах, которые приводят к вибрации сердечника (магнитострикции) в слышимом диапазоне, усиливая гул.
Тормоз для двигателя: Гармоники обратной последовательности (5-я, 11-я и т.д.) создают в асинхронном двигателе магнитное поле, вращающееся *против* основного поля. Это создает отрицательный (тормозной) момент, что снижает КПД, увеличивает нагрев и вызывает вибрации.
«K-фактор»: Для трансформаторов, работающих с нелинейными нагрузками, вводится специальный параметр «K-фактор». Он показывает способность трансформатора выдерживать дополнительные потери и нагрев, вызванные гармоническими токами, без перегрева.
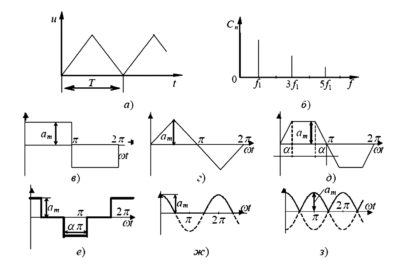
Идеальный «меандр» и гармоники: Идеальный прямоугольный сигнал (меандр) состоит только из *нечетных* гармоник (1-й, 3-й, 5-й, 7-й и т.д.), амплитуда которых убывает обратно пропорционально их номеру ( $ 1/n $ ).
Гармоники и счетчики: Старые индукционные (дисковые) счетчики электроэнергии не всегда корректно учитывали энергию высших гармоник, что приводило к погрешностям в учете. Современные электронные счетчики измеряют полную (активную и реактивную) мощность с учетом гармонических искажений.

FAQ: Часто задаваемые вопросы

1. Что такое коэффициент нелинейных искажений (THD)?

Коэффициент нелинейных искажений (THD, Total Harmonic Distortion) — это ключевой показатель, описывающий степень «загрязнения» синусоидального сигнала высшими гармониками. Он вычисляется как отношение среднеквадратичного значения суммы всех высших гармоник к среднеквадратичному значению основной (первой) гармоники.
$$ \text{THD}_U = \frac{\sqrt{\sum_{n=2}^{\infty} U_n^2}}{U_1} \cdot 100\% $$
Чем выше THD, тем сильнее форма сигнала отличается от идеальной синусоиды.

2. Какие устройства в быту и промышленности создают больше всего гармоник?

Основными «генераторами» гармоник являются нелинейные нагрузки. К ним относятся:

В быту: Импульсные блоки питания (зарядные устройства телефонов, компьютеры, телевизоры), светодиодные (LED) и компактные люминесцентные (КЛЛ) лампы, диммеры (регуляторы света).
В промышленности: Выпрямители, преобразователи частоты для управления двигателями, сварочные аппараты, дуговые сталеплавильные печи, мощные ИБП.

3. Почему гармоники, кратные трем, так опасны для нейтрального провода?

В обычной симметричной трехфазной системе с линейной нагрузкой (например, нагреватели) токи в фазах сдвинуты на 120° и их геометрическая (векторная) сумма в нейтрали равна нулю. Проектировщики часто рассчитывали, что ток в нейтрали будет небольшим. Однако гармоники, кратные трем (3-я, 9-я и т.д.), от всех трех фаз совпадают по фазе. В результате они не компенсируют, а арифметически складываются в нейтральном проводе, создавая ток, который может быть в 3 раза выше фазного тока этой гармоники. Это приводит к перегреву нейтрали, разрушению изоляции и риску возгорания.

4. Как можно измерить уровень гармоник в сети?

Для измерения гармоник используются специальные приборы — анализаторы качества электроэнергии. Это сложные многофункциональные устройства, которые могут в реальном времени выполнять быстрое преобразование Фурье (БПФ) сигнала напряжения или тока и отображать спектр — то есть амплитуды и фазы каждой гармоники в отдельности, а также рассчитывать THD и другие параметры.

5. Какие существуют методы борьбы с высшими гармониками?

Борьба с гармониками — важная задача инженерии. Основные методы:

Пассивные фильтры: Установка LC-фильтров (конденсатор и реактор), настроенных на частоту конкретной гармоники (например, 5-й или 7-й), чтобы «отвести» ее ток на землю.
Активные фильтры: Сложные электронные устройства, которые «измеряют» гармоники и генерируют ток в противофазе, активно компенсируя искажения.
Многопульсные схемы выпрямления: Использование 12-ти, 18-ти или 24-пульсных выпрямителей вместо 6-пульсных, что позволяет взаимно скомпенсировать гармоники низких порядков.
Использование K-факторных трансформаторов: Трансформаторы, специально разработанные для работы с высокими гармоническими токами.

Заключение

Анализ периодических несинусоидальных токов является фундаментальной задачей современной электротехники. Понимание того, как несинусоидальный сигнал раскладывается на гармонические составляющие, и знание особенностей их поведения в трехфазных системах (особенно разделение на прямую, обратную и нулевую последовательности) имеет решающее практическое значение.

Особое внимание к гармоникам, кратным трем, обусловлено их способностью суммироваться в нейтральном проводе и вызывать его опасный перегрев, а также создавать помехи для линий связи. Грамотный расчет, проектирование сетей с учетом нелинейных нагрузок и применение методов фильтрации гармоник в соответствии с действующими стандартами (такими как ГОСТ 32144-2013) являются обязательными условиями для обеспечения надежности, экономичности и электромагнитной совместимости современных систем электроснабжения.

Нормативные документы

ГОСТ 32144-2013 «Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения».
ГОСТ Р 51317.3.4-2006 (IEC 61000-3-4:1998) «Совместимость технических средств электромагнитная. Ограничение эмиссии гармонических составляющих тока техническими средствами с потребляемым током более 16 А, подключаемыми к низковольтным системам электроснабжения. Нормы и методы испытаний».

Периодические несинусоидальные токи и напряжения в трехфазных цепях