Параллельное включение элементов R, L, C в цепях переменного тока

Содержание страницы

1. Теоретические основы метода проводимостей
2. Преобразование схем замещения
3. Практические примеры расчетов
4. Сравнительный анализ последовательного и параллельного соединений R, L, C
5. Преимущества и недостатки параллельного включения нагрузок
6. Интересные факты о параллельных цепях
7. Часто задаваемые вопросы (FAQ)
Заключение

Параллельное соединение элементов является основным способом подключения потребителей в современных электрических сетях низкого и среднего напряжения. В отличие от последовательных цепей, где общим является ток, здесь базовым параметром служит напряжение, что соответствует реальным условиям эксплуатации промышленного и бытового оборудования, рассчитанного на стандартное номинальное напряжение (например, 230/400 В согласно ГОСТ 29322-2014). Понимание физических процессов в таких цепях критически важно для задач энергосбережения, в частности, при компенсации реактивной мощности на предприятиях.

1. Теоретические основы метода проводимостей

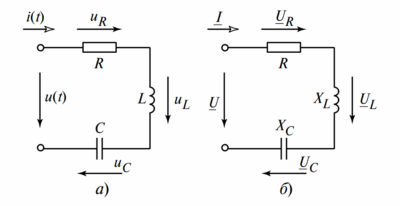
При анализе сложных цепей переменного тока с параллельными ветвями использование классического метода сопротивлений (импедансов) часто приводит к громоздким вычислениям. Более эффективным является метод проводимостей (адмиттансов). В параллельной цепи (рис. 1а) напряжение $ U $ на всех элементах одинаково, а общий ток $ I $ равен геометрической (векторной) сумме токов отдельных ветвей.

Токи в ветвях имеют различные фазовые сдвиги по отношению к общему напряжению:

Ток через активное сопротивление $ I_R $ совпадает по фазе с напряжением.
Ток через идеальную индуктивность $ I_L $ отстает от напряжения на 90°.
Ток через емкость $ I_C $ опережает напряжение на 90°.

В комплексной форме эти токи записываются с использованием понятия проводимостей:

$$ \dot{I}_R = \dot{U}g; \quad \dot{I}_L = \dot{U}(-jb_L); \quad \dot{I}_C = \dot{U}(jb_C) $$

Где введены следующие параметры (единица измерения — сименс, См):

$ g = 1/R $ — активная проводимость;
$ b_L = 1/(\omega L) $ — индуктивная проводимость;
$ b_C = \omega C $ — емкостная проводимость.

Суммарный ток в цепи определяется согласно первому закону Кирхгофа в комплексной форме:

$$ \dot{I} = \dot{I}_R + \dot{I}_L + \dot{I}_C = \dot{U}[g — j(b_L — b_C)] = \dot{U}(g — jb) = \dot{U}Y $$

Здесь $ b = b_L — b_C $ — суммарная реактивная проводимость цепи, а $ Y = \sqrt{g^2 + b^2} $ — полная проводимость цепи. Важно отметить, что знак реактивной проводимости в данной записи противоположен знаку реактивного сопротивления в последовательной цепи, что является особенностью принятой математической модели.

Треугольник проводимостей

По аналогии с треугольником сопротивлений, активная $ g $, реактивная $ b $ и полная $ Y $ проводимости образуют прямоугольный треугольник проводимостей (рис. 1б). Из него следуют основные соотношения для коэффициента мощности:

$$ \cos\phi = \frac{g}{Y}; \quad \sin\phi = \frac{b}{Y}; \quad \text{tg}\phi = \frac{b}{g}; \quad Y = \sqrt{g^2 + b^2} $$

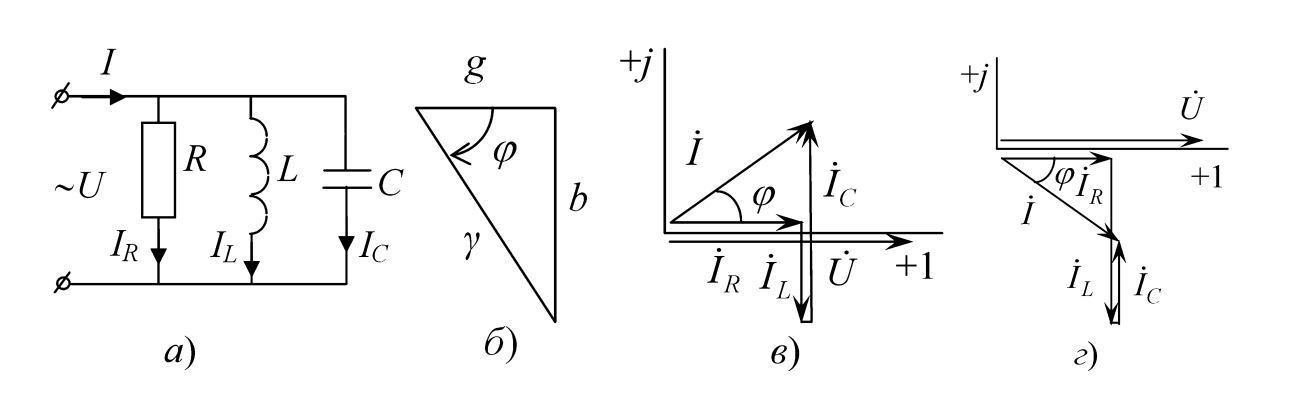
а — принципиальная схема цепи с параллельными ветвями R, L, C;
б — треугольник проводимостей (гипотенуза Y, катеты g и b);
в — векторная диаграмма токов для случая IL < IC (емкостный характер);
г — векторная диаграмма токов для случая IL > IC (индуктивный характер).)

Рисунок 1 — Параллельное включение элементов R, L, C и его характеристики

Векторные диаграммы

Построение векторной диаграммы (рис. 1в, 1г) начинается с вектора напряжения $ \dot{U} $, который принято располагать горизонтально. Относительно него откладываются векторы токов:

Вектор $ \dot{I}_R $ совпадает с вектором $ \dot{U} $.
Вектор $ \dot{I}_L $ отстает на 90° (направлен вниз).
Вектор $ \dot{I}_C $ опережает на 90° (направлен вверх).

Результирующий вектор тока $ \dot{I} $ определяет общий характер цепи. Если $ b_L > b_C $ (индуктивность преобладает), ток отстает от напряжения (активно-индуктивный характер, рис. 1г). Если $ b_C > b_L $, ток опережает напряжение (активно-емкостный характер, рис. 1в).

2. Преобразование схем замещения

Реальные катушки индуктивности обладают активным сопротивлением и изначально представляются последовательной схемой замещения $ R_k + jX_L $. Для удобства расчетов параллельных цепей такую ветвь часто преобразуют в эквивалентную параллельную.

Если известно комплексное сопротивление ветви $ Z = R + jX $, то ее комплексная проводимость $ Y $ равна:

$$ Y = \frac{1}{Z} = \frac{1}{R + jX} = \frac{R — jX}{(R + jX)(R — jX)} = \frac{R}{R^2 + X^2} — j\frac{X}{R^2 + X^2} = g — jb $$

Отсюда получаем формулы пересчета параметров последовательной схемы в параллельную:

$$ g = \frac{R}{R^2 + X^2} = \frac{R}{Z^2}; \quad b = \frac{X}{R^2 + X^2} = \frac{X}{Z^2} $$

Эквивалентность схем означает, что при одинаковом приложенном напряжении они потребляют одинаковый по величине и фазе ток и одинаковую мощность.

3. Практические примеры расчетов

Пример 3.1: Расчет цепи с реальной катушкой и конденсатором

Задача: В сеть с напряжением $ U = 220 $ В и частотой $ f = 50 $ Гц включены параллельно реальная катушка индуктивности ($ R_k = 10 $ Ом, $ L = 0,1 $ Гн) и конденсатор ($ C = 50 $ мкФ). Определить токи в ветвях и общий ток.

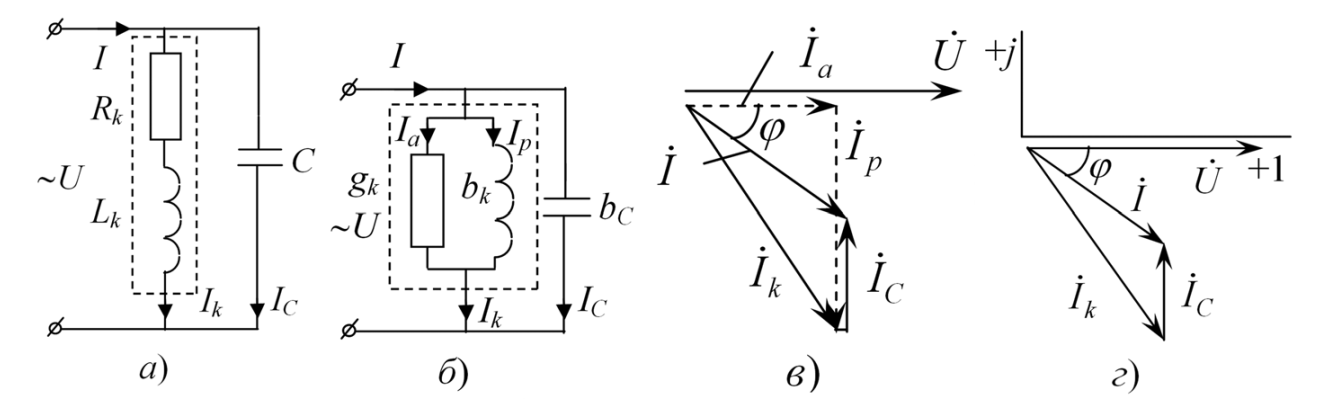
а — исходная схема цепи: параллельно включены ветвь с R_k и L, и ветвь с C;
б — преобразованная схема: три параллельные ветви с проводимостями g_k, b_k и b_c;
в — векторная диаграмма для преобразованной схемы;
г — векторная диаграмма для исходной схемы.

Рисунок 2 — Параллельное включение конденсатора и реальной катушки индуктивности

Решение:

Расчет параметров катушки:
Индуктивное сопротивление: $ X_L = \omega L = 2\pi f L = 314 \cdot 0,1 = 31,4 $ Ом.
Полное сопротивление катушки: $ Z_k = \sqrt{R_k^2 + X_L^2} = \sqrt{10^2 + 31,4^2} \approx 33 $ Ом.
Комплексная проводимость катушки:
$$ Y_k = \frac{1}{Z_k} = \frac{1}{10 + j31,4} = \frac{10 — j31,4}{10^2 + 31,4^2} \approx 0,0091 — j0,0286 \text{ См} $$
Где $ g_k = 0,0091 $ См, $ b_k = 0,0286 $ См.
Расчет проводимости конденсатора:
$ b_c = \omega C = 314 \cdot 50 \cdot 10^{-6} = 0,0157 $ См.
Определение токов (действующие значения):
Активная составляющая тока катушки: $ I_a = g_k U = 0,0091 \cdot 220 \approx 2 $ А.
Реактивная (индуктивная) составляющая тока катушки: $ I_{pk} = b_k U = 0,0286 \cdot 220 \approx 6,3 $ А.
Полный ток катушки: $ I_k = \sqrt{I_a^2 + I_{pk}^2} = \sqrt{2^2 + 6,3^2} \approx 6,6 $ А.
Ток конденсатора: $ I_c = b_c U = 0,0157 \cdot 220 \approx 3,45 $ А.
Расчет общего тока:
Общий реактивный ток: $ I_p = I_{pk} — I_c = 6,3 — 3,45 = 2,85 $ А (индуктивный характер).
Общий ток: $ I = \sqrt{I_a^2 + I_p^2} = \sqrt{2^2 + 2,85^2} \approx 3,48 $ А.

Обратите внимание: общий ток (3,48 А) значительно меньше арифметической суммы токов ветвей (6,6 + 3,45 = 10,05 А). Это явление частичной взаимной компенсации реактивных токов лежит в основе методов повышения энергоэффективности.

Пример 3.2: Компенсация реактивной мощности в промышленности

Задача: Цех потребляет активную мощность $ P = 200 $ кВт при напряжении $ U = 220 $ В и токе $ I = 2000 $ А. Определить исходный коэффициент мощности и рассчитать его новое значение после подключения конденсаторной батареи емкостью $ C = 0,02 $ Ф.

Решение (анализ трех методов):

Исходное состояние: Полная мощность $ S = U \cdot I = 220 \cdot 2000 = 440 $ кВА. Коэффициент мощности $ \cos\phi_1 = P/S = 200000 / 440000 \approx 0,45 $. Это крайне низкое значение, указывающее на высокую загрузку сети реактивным током.

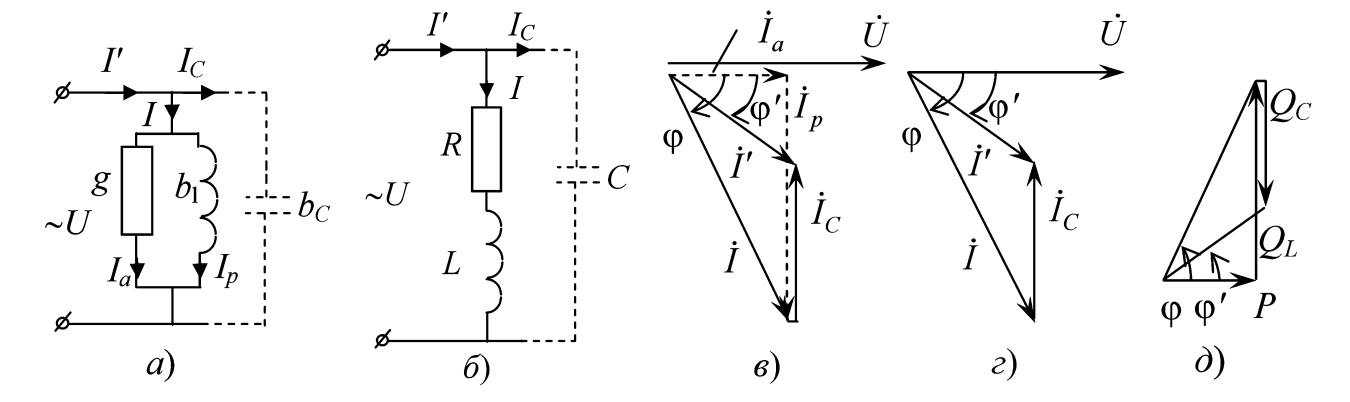
а — параллельная схема замещения потребителей цеха;
б — последовательная схема замещения потребителей;
в — векторная диаграмма токов при использовании параллельной схемы замещения;
г — векторная диаграмма при использовании последовательной схемы;
д — треугольник мощностей, показывающий уменьшение реактивной мощности Q.

Рисунок 3 — Компенсация реактивной мощности предприятия

Подключение батареи конденсаторов:

Метод проекций токов:
Активный ток нагрузки: $ I_a = I \cdot \cos\phi_1 = 2000 \cdot 0,45 = 900 $ А.
Реактивный (индуктивный) ток нагрузки: $ I_{L} = I \cdot \sin\phi_1 = 2000 \cdot \sqrt{1-0,45^2} \approx 1782 $ А.
Ток конденсаторной батареи: $ I_C = U \cdot \omega C = 220 \cdot 314 \cdot 0,02 \approx 1382 $ А.
Новый реактивный ток: $ I’_p = I_L — I_C = 1782 — 1382 = 400 $ А.
Новый общий ток: $ I’ = \sqrt{I_a^2 + (I’_p)^2} = \sqrt{900^2 + 400^2} \approx 985 $ А.
Новый коэффициент мощности: $ \cos\phi_2 = I_a / I’ = 900 / 985 \approx 0,92 $.
Метод мощностей (наиболее применим на практике):
Исходная реактивная мощность: $ Q_1 = P \cdot \text{tg}\phi_1 \approx 200 \cdot 1,98 \approx 396 $ кВАр (в примере из источника использован иной метод округления, дающий 398 кВАр).
Мощность конденсаторной батареи: $ Q_C = U^2 \cdot \omega C = 220^2 \cdot 314 \cdot 0,02 \approx 304 $ кВАр.
Остаточная реактивная мощность: $ Q_2 = Q_1 — Q_C = 398 — 304 = 94 $ кВАр.
Новый угол: $ \text{tg}\phi_2 = Q_2 / P = 94000 / 200000 = 0,47 $, откуда $ \phi_2 \approx 25^\circ $, $ \cos\phi_2 \approx 0,91…0,92 $.

Результат: Подключение конденсаторов снизило потребляемый ток с 2000 А до 985 А при сохранении той же полезной активной мощности. Это значительно снижает потери в подводящих линиях и трансформаторах.

4. Сравнительный анализ последовательного и параллельного соединений R, L, C

Таблица 1 — Сравнение свойств последовательной и параллельной цепей RLC
Характеристика	Последовательное соединение	Параллельное соединение
Общий параметр	Ток $ I $ (одинаков для всех элементов)	Напряжение $ U $ (одинаково для всех элементов)
Основной закон	Второй закон Кирхгофа для напряжений: $ \dot{U} = \Sigma \dot{U}_k $	Первый закон Кирхгофа для токов: $ \dot{I} = \Sigma \dot{I}_k $
Резонанс	Резонанс напряжений (возможны $ U_L, U_C \gg U_{вх} $)	Резонанс токов (возможны $ I_L, I_C \gg I_{общ} $)
Эквивалентный параметр	Импеданс $ Z = \sqrt{R^2 + (X_L — X_C)^2} $	Адмиттанс $ Y = \sqrt{g^2 + (b_C — b_L)^2} $
Применение	Частотные фильтры, ограничители тока	Распределение электроэнергии, компенсация реактивной мощности

5. Преимущества и недостатки параллельного включения нагрузок

Преимущества:

Независимость работы: Отключение одного потребителя не влияет на работу остальных (при условии достаточной мощности источника).
Стандартизация напряжения: Все потребители рассчитываются на одно номинальное напряжение (например, 230 В), что упрощает их производство и эксплуатацию.
Возможность локальной компенсации: Реактивную мощность можно компенсировать непосредственно у места её потребления.

Недостатки:

Суммирование токов: Подключение каждого нового потребителя увеличивает общий ток источника, что требует проводов большего сечения.
Опасность токового резонанса: При неверном расчете компенсирующих устройств возможно возникновение резонанса токов, при котором внутренние токи контура между индуктивностью и емкостью могут многократно превышать номинальные значения, вызывая перегрев и аварии.

6. Интересные факты о параллельных цепях

«Война токов» и победа параллельности: Одной из причин победы системы переменного тока Теслы/Вестингауза над постоянным током Эдисона была возможность легкой трансформации напряжения, что позволило экономично реализовать именно параллельную систему распределения энергии для независимых потребителей.
Резонанс токов как «затычка»: Идеальный параллельный LC-контур на резонансной частоте имеет бесконечно большое сопротивление для внешнего источника, фактически блокируя протекание тока этой частоты. Это используется в заграждающих фильтрах.
Косинус «фи» и штрафы: Крупные промышленные предприятия платят штрафы энергоснабжающим организациям, если их коэффициент мощности ниже установленного норматива (обычно 0,92–0,95), так как они перегружают сети «бесполезным» реактивным током.
Синхронные компенсаторы: Кроме конденсаторов, для компенсации реактивной мощности в больших энергосистемах используются синхронные двигатели, работающие в режиме перевозбуждения (параллельно нагрузке).
Суперконденсаторы в параллель: В современном электротранспорте параллельно аккумуляторам включают блоки ионисторов (суперконденсаторов) для покрытия пиковых токовых нагрузок при разгоне.
Опасность обрыва нуля: В трехфазных сетях при соединении нагрузок звездой (разновидность параллельного включения фаз) обрыв нулевого провода приводит к «перекосу фаз», когда на одних потребителях напряжение падает, а на других может возрасти до 380 В и выше.
Паразитные параметры: На высоких частотах любой реальный резистор имеет паразитную параллельную емкость, а катушка индуктивности — межвитковую емкость, что превращает их в сложные параллельные RLC-контуры со своими резонансами.

7. Часто задаваемые вопросы (FAQ)

Почему в квартирах используется только параллельное соединение розеток и ламп?

Это обеспечивает независимость их работы. Если бы они были включены последовательно, перегорание одной лампочки обесточило бы всю квартиру, а напряжение на каждом приборе зависело бы от их количества и мощности.

Что такое активная и реактивная проводимость простыми словами?

Активная проводимость (g) показывает способность цепи безвозвратно потреблять энергию (на нагрев, механическую работу). Реактивная проводимость (b) показывает способность цепи обмениваться энергией между источником и магнитными/электрическими полями без её безвозвратного потребления.

Можно ли измерить реактивный ток обычным амперметром?

Нет, обычный амперметр измеряет полный действующий ток $ I = \sqrt{I_a^2 + I_p^2} $. Разделить его на активную и реактивную составляющие можно только с помощью специализированных приборов — фазометров или анализаторов качества электроэнергии.

Всегда ли нужно стремиться к cos φ = 1?

В теории да, но на практике часто ограничиваются значением 0,95-0,98. Полная компенсация (до 1) может привести к «перекомпенсации» при снижении нагрузки, когда сеть становится емкостной, что может вызвать нежелательное повышение напряжения.

В чем разница между сименсом (См) и омом (Ом)?

Они взаимно обратны. 1 Сименс = 1 / 1 Ом. Если сопротивление элемента 10 Ом, его проводимость 0,1 См.

Что произойдет при резонансе токов в идеальном параллельном контуре?

В идеальном контуре без активного сопротивления (g=0) при резонансе ($ b_L = b_C $) общий ток от источника станет равным нулю, хотя токи внутри контура между L и C могут быть огромными.

Как влияет частота сети на параллельную RLC цепь?

С ростом частоты индуктивная проводимость $ b_L = 1/(\omega L) $ падает, а емкостная $ b_C = \omega C $ растет. Цепь, имевшая индуктивный характер на низкой частоте, может стать емкостной на высокой.

Заключение

Метод проводимостей и векторных диаграмм является мощным инструментом анализа параллельных цепей переменного тока. Он позволяет наглядно представить процессы распределения токов и является базой для инженерных расчетов компенсации реактивной мощности — ключевого мероприятия для повышения эффективности современных систем электроснабжения. Грамотное применение этих знаний позволяет снижать потери энергии, уменьшать сечения кабелей и повышать стабильность напряжения в промышленных сетях.

Нормативная база и литература

ГОСТ R 52002-2003 «Электротехника. Термины и определения основных понятий». (Действующий стандарт, определяющий базовые термины: активная мощность, реактивная мощность, полная проводимость).
ГОСТ 32144-2013 «Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения». (Определяет требования к коэффициенту мощности и гармоническим составляющим).
ПУЭ (Правила устройства электроустановок), издание 7. Раздел 1.2 «Электроснабжение и электрические сети». (Содержит указания по компенсации реактивной мощности).
Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2024.