Содержание страницы
Теория электрических цепей (ТЭЦ) является базисом всей современной электротехники, электроники и радиотехники. Понимание процессов, происходящих в электрических устройствах, невозможно без глубокого усвоения фундаментальных понятий, заложенных в XIX веке великими учеными: Георгом Омом, Густавом Кирхгофом, Андре Ампером и Алессандро Вольтой. Несмотря на колоссальный прогресс в технологиях, базовые уравнения, описывающие равновесие в электрических цепях, остаются неизменными.
В современной инженерной практике классическая теория цепей дополняется методами компьютерного моделирования, однако адекватность любой модели зависит от правильности понимания физических процессов инженером. Данный материал представляет собой углубленное техническое руководство по основным законам и элементам электрических цепей, актуализированное с учетом современной нормативной базы и инженерных подходов.
1. Базовые определения и топология цепей
1.1. Электрическая цепь: современная трактовка
В настоящее время актуальным стандартом базовых определений является ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий», который гармонизирован с международными стандартами. Согласно современной нормативной базе:
Ключевым условием существования электрической цепи является наличие замкнутого контура для протекания тока. Важно различать физическую реализацию и ее графическое представление:
- Электрическая цепь — реальная совокупность физических устройств (генераторы, линии передачи, потребители).
- Электрическая схема — графическое изображение цепи с использованием условных обозначений (регулируется стандартами ЕСКД, в частности ГОСТ 2.701-2008 и ГОСТ 2.702-2011).
1.2. Ключевые скалярные величины
Состояние цепи в любой момент времени характеризуется мгновенными значениями тока и напряжения, которые являются функциями времени: \( u = u(t) \) и \( i = i(t) \). Для цепей постоянного тока эти значения неизменны во времени и обозначаются прописными буквами \( U \) и \( I \).
Электродвижущая сила (ЭДС)
Источники энергии характеризуются ЭДС. Физически ЭДС — это работа сторонних сил (неэлектростатического происхождения) по перемещению единичного положительного заряда от меньшего потенциала к большему внутри источника. Природа этих сил может быть различной: химической (в аккумуляторах), электромагнитной (в генераторах), тепловой (в термопарах).
\[ e(t) = \frac{dw_{стор}}{dq} \]
Численно ЭДС равна напряжению на зажимах идеализированного источника при разомкнутой внешней цепи (режим холостого хода). Направление ЭДС всегда совпадает с направлением перемещения положительных зарядов внутри источника (от «минуса» к «плюсу»).
Электрический ток
Ток — это упорядоченное движение носителей заряда. Количественно мгновенное значение тока определяется как скорость изменения заряда \( q \) через поперечное сечение проводника:
\[ i(t) = \frac{dq}{dt} \]
Важно: За условно-положительное направление тока исторически принято направление движения положительных зарядов. В металлических проводниках реальными носителями являются электроны, движущиеся в противоположном направлении. В расчетах направление тока выбирается произвольно; если в результате вычислений значение тока получается отрицательным, значит, истинное направление противоположно выбранному.
Электрическое напряжение и потенциал
Напряжение между двумя точками цепи — это работа электрического поля по перемещению единичного пробного заряда между этими точками.
\[ u = \frac{dw}{dq} \]
Напряжение также можно определить через разность потенциалов. Потенциал \( \phi \) — это энергетическая характеристика точки поля:
\[ \phi = \frac{w_п}{q} \]
Тогда напряжение между точками 1 и 2:
\[ u_{12} = \phi_1 — \phi_2 \]
Положительное направление напряжения совпадает с выбранным положительным направлением тока на пассивном участке цепи.
Электрическая мощность
Мгновенная мощность характеризует скорость преобразования энергии в цепи:
\[ p(t) = \frac{dw}{dt} = \frac{dw}{dq} \cdot \frac{dq}{dt} = u(t) \cdot i(t) \]
Если \( p > 0 \), участок цепи потребляет энергию (например, резистор), если \( p < 0 \) — отдает энергию (источник).
1.3. Топологические элементы схемы
Для анализа разветвленных цепей вводят топологические понятия:
- Ветвь — участок цепи, вдоль которого протекает один и тот же ток. Ветвь состоит из последовательно соединенных элементов.
- Узел — место соединения трех и более ветвей. На схемах обозначается точкой.
- Контур — любой замкнутый путь, проходящий по нескольким ветвям.
2. Элементная база теории цепей: модели и реальность
В теории цепей реальные устройства заменяются их математическими моделями — схемами замещения, составленными из идеализированных элементов. Каждый такой элемент отражает один доминирующий физический процесс.
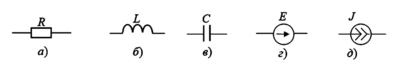
2.1. Пассивные элементы
Пассивные элементы не могут генерировать энергию длительное время, они ее либо рассеивают, либо накапливают.
- Резистивный элемент (R). Учитывает необратимое преобразование электрической энергии в другие виды (преимущественно тепловую). Описывается законом Ома:
\[ u_R(t) = R \cdot i_R(t) \]
Мгновенная мощность всегда положительна: \( p_R = i^2 R = u^2 / R \). - Индуктивный элемент (L). Учитывает энергию магнитного поля, создаваемого током. Характеризуется индуктивностью \( L = \Psi / i \), где \( \Psi \) — потокосцепление.
Связь напряжения и тока (закон электромагнитной индукции Фарадея):
\[ u_L(t) = \frac{d\Psi}{dt} = L \frac{di_L(t)}{dt} \]
Энергия магнитного поля: \( W_M = \frac{L i^2}{2} \). - Емкостный элемент (C). Учитывает энергию электрического поля. Характеризуется емкостью \( C = q / u \).
Ток через емкость пропорционален скорости изменения напряжения:
\[ i_C(t) = \frac{dq}{dt} = C \frac{du_C(t)}{dt} \]
Энергия электрического поля: \( W_Э = \frac{C u^2}{2} \).
2.2. Активные элементы (источники)
Источники энергии в теории цепей делятся на два идеализированных типа:
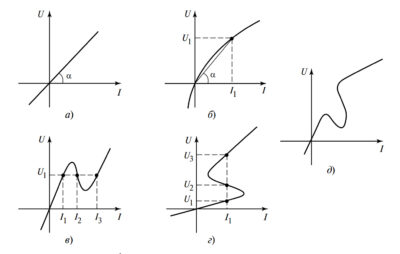
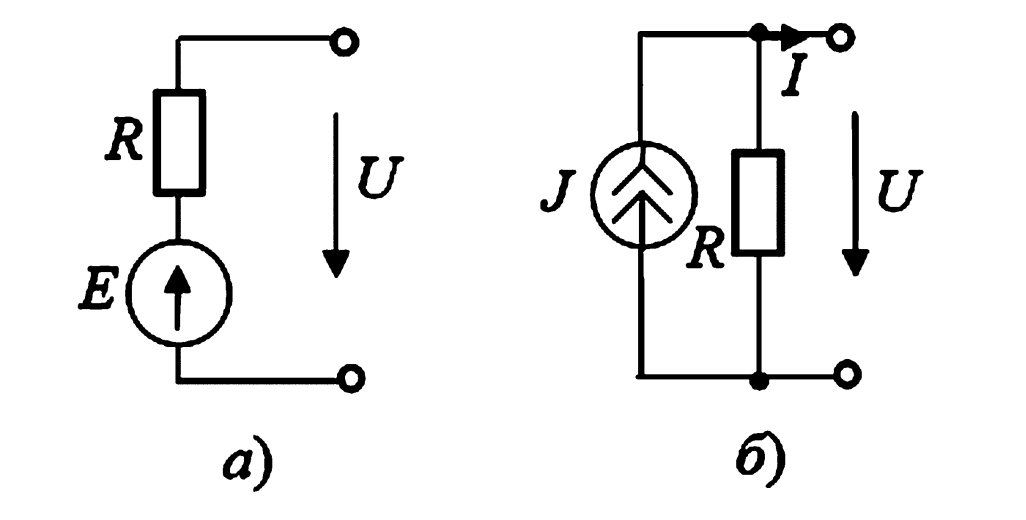
- Идеальный источник ЭДС (напряжения). Поддерживает на своих зажимах заданное напряжение \( u(t) = e(t) \) независимо от величины протекающего тока. Его внутреннее сопротивление равно нулю. Внешняя характеристика — горизонтальная прямая (рис. 2, б).
- Идеальный источник тока. Создает заданный ток \( i(t) = J(t) \) независимо от напряжения на его зажимах. Его внутреннее сопротивление бесконечно велико. Внешняя характеристика — вертикальная прямая (рис. 2, в).
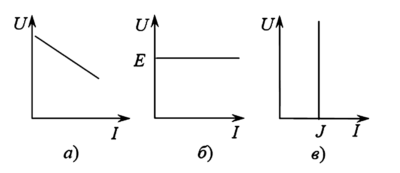
Реальный источник (например, аккумулятор) имеет падающую внешнюю характеристику (рис. 2, а) и может быть представлен двумя эквивалентными схемами замещения (рис. 3):
- Последовательным соединением идеального источника ЭДС \( E \) и внутреннего сопротивления \( R_{вн} \) (модель Тевенина). Уравнение: \( U = E — I \cdot R_{вн} \).
- Параллельным соединением идеального источника тока \( J \) и внутренней проводимости \( G_{вн} = 1/R_{вн} \) (модель Нортона). Ток источника \( J = E / R_{вн} \).
3. Фундаментальные законы электрических цепей
Математическое моделирование цепей базируется на двух типах уравнений: компонентных (закон Ома) и топологических (законы Кирхгофа).
3.1. Закон Ома
Устанавливает связь между током и напряжением на отдельном элементе. В общем виде для участка цепи с ЭДС:
\[ I = \frac{U_{ab} + \sum E}{R_{ab}} \]
В дифференциальной форме для реактивных элементов закон Ома трансформируется в уравнения (1.7) и (1.8), приведенные выше.
3.2. Законы Кирхгофа
Эти законы являются следствием фундаментального закона сохранения энергии и заряда.
Первый закон Кирхгофа (ЗК1) — баланс токов
Алгебраическая сумма токов в любом узле электрической цепи равна нулю. Это означает, что заряд в узле не накапливается.
\[ \sum_{k=1}^{n} i_k(t) = 0 \]
Токи, направленные к узлу, обычно берут со знаком «+», а от узла — со знаком «–» (или наоборот, важно соблюдать единообразие).
Второй закон Кирхгофа (ЗК2) — баланс напряжений
Алгебраическая сумма падений напряжений вдоль любого замкнутого контура равна алгебраической сумме ЭДС в этом же контуре:
\[ \sum_{k} R_k i_k = \sum_{k} e_k \]
Или в более общем виде, сумма напряжений на всех элементах контура равна нулю:
\[ \sum_{k} u_k(t) = 0 \]
При составлении уравнений по ЗК2 выбирают произвольное направление обхода контура. Если направление тока в ветви (или направление ЭДС) совпадает с обходом, слагаемое берется с «+», иначе — с «–».
3.3. Обобщенный закон Кирхгофа для участка цепи
Иногда необходимо найти напряжение не в замкнутом контуре, а между двумя произвольными точками схемы. Рассмотрим участок цепи между точками a и c (рис. 4, а).
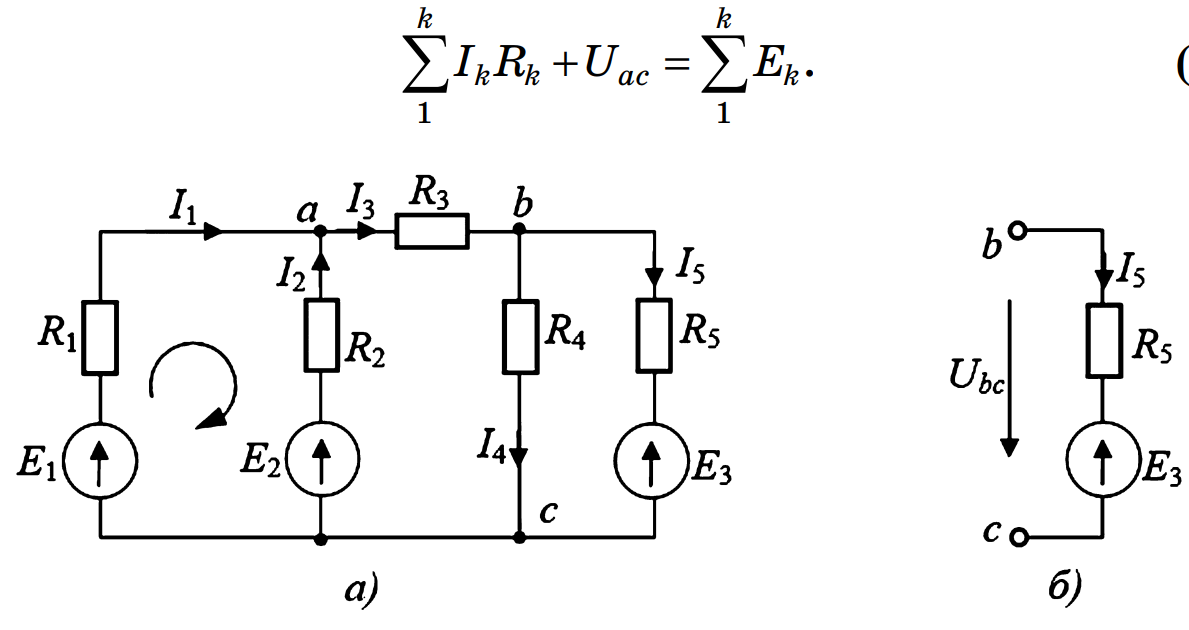
Напряжение \( U_{ac} \) можно найти, «пройдя» по любому пути от точки a к точке c, суммируя потенциалы. Согласно уравнению из исходного материала:
\[ \sum I_k R_k + U_{ac} = \sum E_k \]
Для отдельной ветви (рис. 1.4, б) уравнение баланса напряжений при обходе по часовой стрелке:
\[ I_5 R_5 — U_{bc} = -E_5 \quad \Rightarrow \quad U_{bc} = E_5 + I_5 R_5 \]
4. Сравнительный анализ и особенности применения
Таблица 1 — Сравнение свойств базовых пассивных элементов
| Свойство | Резистор (R) | Индуктивность (L) | Емкость (C) |
|---|---|---|---|
| Основная функция | Ограничение тока, рассеивание энергии | Накопление магнитной энергии, инерция тока | Накопление электрической энергии, инерция напряжения |
| Энергетический процесс | Диссипация (необратимый) | Накопление (реактивный) | Накопление (реактивный) |
| Поведение на постоянном токе | Проводит ток согласно \( I=U/R \) | Короткое замыкание (\( R \approx 0 \)) | Разрыв цепи (\( R \to \infty \)) |
| Фазовый сдвиг (синусоидальный ток) | Ток и напряжение в фазе (0°) | Напряжение опережает ток на 90° | Ток опережает напряжение на 90° |
Преимущества и недостатки идеализированных моделей
Преимущества:
- Существенное упрощение математического аппарата (использование линейных алгебраических или дифференциальных уравнений с постоянными коэффициентами).
- Возможность применения унифицированных методов анализа (метод узловых потенциалов, метод контурных токов).
- Наглядность физических процессов.
Недостатки и ограничения:
- Игнорирование паразитных параметров может привести к значительным погрешностям на высоких частотах или в переходных режимах.
- Нелинейные эффекты (насыщение магнитопроводов, температурная зависимость сопротивления) требуют усложнения моделей.
- Модели с сосредоточенными параметрами неприменимы для длинных линий, где длина волны электромагнитного колебания соизмерима с геометрическими размерами цепи.
5. Интересные факты о теории цепей
- Молодость гения: Густав Кирхгоф сформулировал свои знаменитые законы в 1845 году, будучи 21-летним студентом. Они стали развитием работ Георга Ома.
- Скорость тока vs Скорость электронов: Электрический сигнал (электромагнитное поле) распространяется по цепи со скоростью, близкой к скорости света (около 300 000 км/с в вакууме). При этом сама скорость дрейфа электронов в проводнике составляет доли миллиметра в секунду.
- Война токов: В конце XIX века шла ожесточенная «война токов» между Томасом Эдисоном (постоянный ток) и Николой Теслой с Джорджем Вестингаузом (переменный ток). Победа переменного тока обусловлена простотой трансформации напряжения, что критично для передачи энергии на большие расстояния.
- «Четвертый элемент»: Долгое время считалось, что базовых пассивных элементов всего три: резистор (связь u-i), конденсатор (связь q-u) и индуктивность (связь Ψ-i). Однако в 1971 году профессор Леон Чуа теоретически предсказал существование четвертого фундаментального элемента — мемристора, который должен устанавливать прямую связь между зарядом и магнитным потоком (dΨ = M dq). Физически реализовать его удалось только в 2008 году в лабораториях HP.
- Непризнанный гений Ома: Когда Георг Ом в 1827 году опубликовал свой фундаментальный труд, он встретил не просто скептицизм, а враждебность. Его математический подход к физике тогда считался «ересью», министр образования Германии даже заявил, что «физик, проповедующий подобную ересь, недостоин преподавать науку». Признание пришло к Ому только спустя почти 20 лет.
- Вечный ток: В теории идеальная индуктивность (R=0) может хранить энергию вечно. На практике это реализуется в сверхпроводящих кольцах. Эксперименты показали, что однажды наведенный ток в сверхпроводящем контуре может циркулировать без затухания годами (расчетное время затухания — не менее 100 000 лет), что является лучшим физическим приближением к идеальной модели индуктивности.
6. FAQ: Часто задаваемые вопросы
Заключение
Рассмотренные в данном руководстве основные понятия и законы — это алфавит электротехники. Уверенное владение законом Ома, законами Кирхгофа и понимание физической сути R, L, C элементов позволяет инженеру анализировать устройства любой сложности: от простейшего фонарика до микропроцессора, который содержит миллиарды транзисторов, каждый из которых можно представить упрощенной схемой замещения.
Современная электроника все больше уходит в область высоких частот и наноразмеров, где классические модели требуют уточнений, но фундамент, заложенный классической теорией цепей, остается незыблемым.
Нормативная база
- ГОСТ Р 52002-2003. Электротехника. Термины и определения основных понятий.
- ГОСТ 2.702-2011. Единая система конструкторской документации (ЕСКД). Правила выполнения электрических схем.
- ГОСТ IEC 60050. Международный электротехнический словарь (серия стандартов).
Список литературы
- Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2023.
- Демирчян К.С., Нейман Л.Р., Коровкин Н.В. Теоретические основы электротехники. В 3-х т. — СПб.: Питер, 2019.