Операторный метод (преобразование Лапласа) в электротехнике

Содержание страницы

Сущность операторного метода на основе преобразования Лапласа
Расчет цепей операторным методом
Передаточные функции и временные характеристики
Преимущества и недостатки операторного метода
Сравнение операторного и классического методов
Интересные факты по теме
Часто задаваемые вопросы (FAQ)
Заключение

Операторный метод — это мощный математический инструмент, используемый в электротехнике, теории управления и других областях инженерии для анализа переходных процессов. Суть метода заключается в применении интегрального преобразования Лапласа, которое позволяет заменить сложные дифференциальные и интегральные уравнения, описывающие электрическую цепь, на более простые алгебраические уравнения.

Исторически, основы интегральных преобразований были заложены Пьером-Симоном Лапласом в конце XVIII века. Однако практическое применение в электротехнике метод получил благодаря работам Оливера Хевисайда в конце XIX века, который разработал «операционное исчисление» для решения задач телеграфии. Современный операторный метод, основанный на строгой теории преобразования Лапласа, стал стандартом для инженеров в XX веке.

Сущность операторного метода на основе преобразования Лапласа

Метод базируется на замене функций времени $f(t)$ (оригиналов) функциями комплексной частоты $p = \sigma + j\omega$ (изображений) с помощью прямого преобразования Лапласа:

$$F(p) = \int_{0}^{\infty} f(t) e^{-pt} dt$$

Ключевое преимущество этого перехода заключается в том, что операции дифференцирования и интегрирования во временной области (области оригиналов) заменяются алгебраическими операциями умножения и деления в области комплексной частоты (области изображений):

Дифференцирование $\frac{d}{dt}$ заменяется умножением на $p$.
Интегрирование $\int dt$ заменяется делением на $p$.

Это позволяет преобразовать исходную систему линейных дифференциальных уравнений, описывающих цепь, в систему алгебраических уравнений относительно изображений искомых токов и напряжений.

После решения этой алгебраической системы и нахождения изображения искомой величины (например, $I(p)$ или $U(p)$), выполняется переход обратно во временную область с помощью обратного преобразования Лапласа. Этот переход осуществляется по формуле Меллина-Римана:

$$f(t) = \frac{1}{2\pi j} \int_{\sigma — j\infty}^{\sigma + j\infty} F(p) e^{pt} dp$$

На практике этот сложный интеграл редко вычисляют напрямую. Вместо этого используют таблицы соответствия между изображениями и оригиналами или теорему разложения Хевисайда.

Этот процесс — переход из временной области в частотную, решение алгебраической задачи и возврат во временную область — аналогичен по своей логике использованию логарифмов для упрощения умножения или применению комплексного метода для расчета установившихся синусоидальных режимов.

Соответствие между оригиналом и изображением символически записывают как $F(p) \leftrightarrow f(t)$. Таким образом, функциям $u(t)$ и $i(t)$ соответствуют изображения $U(p)$ и $I(p)$.

Изображения основных функций и операций

Ниже приведены изображения некоторых функций и операций, наиболее часто встречающихся в электротехнике:

№	Оригинал (функция времени) $f(t)$	Изображение (функция частоты) $F(p)$	Описание
1	$\delta(t)$	$1$	Дельта-функция (единичный импульс)
2	$1(t)$	$\frac{1}{p}$	Единичная ступенчатая функция (функция Хевисайда)
3	$A$ (константа)	$\frac{A}{p}$	Постоянная величина (при $t \ge 0$)
4	$t$	$\frac{1}{p^2}$	Линейно нарастающая функция
5	$t^n$	$\frac{n!}{p^{n+1}}$	Степенная функция
6	$e^{-\alpha t}$	$\frac{1}{p + \alpha}$	Затухающая экспонента
7	$t e^{-\alpha t}$	$\frac{1}{(p + \alpha)^2}$
8	$\sin(\omega t)$	$\frac{\omega}{p^2 + \omega^2}$	Синусоида
9	$\cos(\omega t)$	$\frac{p}{p^2 + \omega^2}$	Косинусоида
10	$e^{-\alpha t} \sin(\omega t)$	$\frac{\omega}{(p + \alpha)^2 + \omega^2}$	Затухающая синусоида
11	$e^{-\alpha t} \cos(\omega t)$	$\frac{p + \alpha}{(p + \alpha)^2 + \omega^2}$	Затухающая косинусоида

Изображения дифференцирования и интегрирования

Эти свойства являются основой метода при составлении уравнений цепи:

Изображение производной:
$$\frac{df(t)}{dt} \leftrightarrow pF(p) — f(0)$$
где $f(0)$ — значение функции $f(t)$ в начальный момент времени $t = 0$.
Изображение второй производной:
$$\frac{d^2f(t)}{dt^2} \leftrightarrow p^2F(p) — pf(0) — f'(0)$$
где $f'(0)$ — значение первой производной при $t = 0$.
Изображение интеграла:
$$\int_{0}^{t} f(t) dt \leftrightarrow \frac{F(p)}{p}$$

Операторные модели элементов электрической цепи

На основе формул для производной и интеграла можно определить операторные изображения напряжений на пассивных элементах (R, L, C) при ненулевых начальных условиях.

Резистор (R):$u_R(t) = R \cdot i(t)$
$U_R(p) = R \cdot I(p)$Операторное сопротивление: $Z_R(p) = R$
Индуктивность (L):$u_L(t) = L \frac{di_L(t)}{dt}$
$U_L(p) = L [pI_L(p) — i_L(0)] = pLI_L(p) — Li_L(0)$
где $i_L(0)$ — начальный ток через индуктивность.Операторное сопротивление: $Z_L(p) = pL$
Емкость (C):$u_C(t) = \frac{1}{C} \int_{0}^{t} i_C(t) dt + u_C(0)$
$U_C(p) = \frac{1}{pC} I_C(p) + \frac{u_C(0)}{p}$
где $u_C(0)$ — начальное напряжение на емкости.Операторное сопротивление: $Z_C(p) = \frac{1}{pC}$

Основные теоремы преобразования Лапласа

Теорема смещения в области оригиналов (теорема запаздывания):Если $f(t) \leftrightarrow F(p)$, то функция, задержанная на время $\tau$, имеет изображение:$$f(t — \tau) \leftrightarrow e^{-p\tau} F(p)$$Эта теорема доказывается непосредственным применением преобразования Лапласа.
Теорема смещения в области изображений (теорема затухания):Если $f(t) \leftrightarrow F(p)$, то умножение оригинала на экспоненту соответствует сдвигу в области изображений:$$e^{-\lambda t} f(t) \leftrightarrow F(p + \lambda)$$
Теорема об изменении масштаба (теорема подобия):
$$f(\alpha t) \leftrightarrow \frac{1}{\alpha} F\left(\frac{p}{\alpha}\right)$$
Предельные соотношения (теоремы о начальном и конечном значениях):Эти теоремы позволяют найти начальное $f(0+)$ и установившееся $f(\infty)$ значения оригинала, не находя сам оригинал, а анализируя его изображение $F(p)$.
- Начальное значение: $f(0+) = \lim_{t \to 0} f(t) = \lim_{p \to \infty} [pF(p)]$
- Установившееся значение: $f_{\text{уст}} = f(\infty) = \lim_{t \to \infty} f(t) = \lim_{p \to 0} [pF(p)]$
Установившееся значение, определенное по этой теореме, представляет собой принужденную составляющую переходного процесса.

Расчет цепей операторным методом

Алгоритм расчета

Расчет переходного процесса в сложной цепи операторным методом сводится к следующей последовательности шагов:

Определить независимые начальные условия (токи в индуктивностях $i_L(0)$ и напряжения на емкостях $u_C(0)$) из режима цепи до коммутации.
Составить операторную схему замещения для цепи после коммутации (при $t > 0$). В этой схеме все источники ЭДС и токов заменяются их изображениями, а пассивные элементы R, L, C заменяются их операторными сопротивлениями $R$, $pL$, $1/pC$.
Учесть начальные условия. Это можно сделать двумя способами:
- Способ А: Ввести в операторную схему замещения эквивалентные «внутренние» источники ЭДС или тока, отражающие начальную энергию, запасенную в L и C.
- Способ Б: Составлять уравнения, используя полные операторные модели (например, $U_L(p) = pLI_L(p) — Li_L(0)$), которые уже содержат начальные условия.
Составить систему уравнений для операторной схемы, используя стандартные методы (например, законы Кирхгофа, метод контурных токов, метод узловых потенциалов). Так как схема состоит из алгебраических элементов, система уравнений будет алгебраической, а не дифференциальной.
Решить полученную алгебраическую систему и найти изображение $F(p)$ искомой величины (тока или напряжения).
Выполнить переход от изображения $F(p)$ к оригиналу $f(t)$ с помощью обратного преобразования Лапласа (чаще всего, используя теорему разложения).

Законы Кирхгофа в операторной форме

Рассмотрим дифференциальное уравнение для последовательной RCL-цепи при подключении к постоянному напряжению E (при $t \ge 0$):

$$Ri(t) + L\frac{di(t)}{dt} + \frac{1}{C}\int_{0}^{t} i(t) dt + u_C(0) = E$$

Используя преобразование Лапласа для каждого слагаемого, запишем это уравнение в операторной форме:

$$RI(p) + [pLI(p) — Li(0)] + \frac{1}{pC}I(p) + \frac{u_C(0)}{p} = \frac{E}{p}$$

Группируя слагаемые, получаем:

$$\left(R + pL + \frac{1}{pC}\right)I(p) = \frac{E}{p} + Li(0) — \frac{u_C(0)}{p}$$

Выражение $Z(p) = R + pL + \frac{1}{pC}$ называется операторным сопротивлением цепи. Тогда уравнение можно записать в виде закона Ома в операторной форме:

$$Z(p)I(p) = U(p)_{\text{внеш}} + E(p)_{\text{внутр}}$$

Где $I(p) = \frac{\frac{E}{p} — \frac{u_C(0)}{p} + Li(0)}{Z(p)}$.

Аналогично можно записать законы Кирхгофа для сложных цепей. Для любого k-го узла и любого m-го контура:

Первый закон Кирхгофа: $\sum \pm I_k(p) = 0$
Второй закон Кирхгофа: $\sum \pm Z_k(p)I_k(p) = \sum \pm E_k(p) + \sum \pm E_k(p)_{\text{внутр}}$

В полученных уравнениях, наряду с действующими внешними источниками ЭДС $E_k(p)$, появляются слагаемые, учитывающие начальные условия: $Li(0)$ и $\frac{u_C(0)}{p}$. Их называют внутренними ЭДС и изображают на операторных схемах замещения.

Рисунок 1 — Схемы электрической цепи к примеру 1:
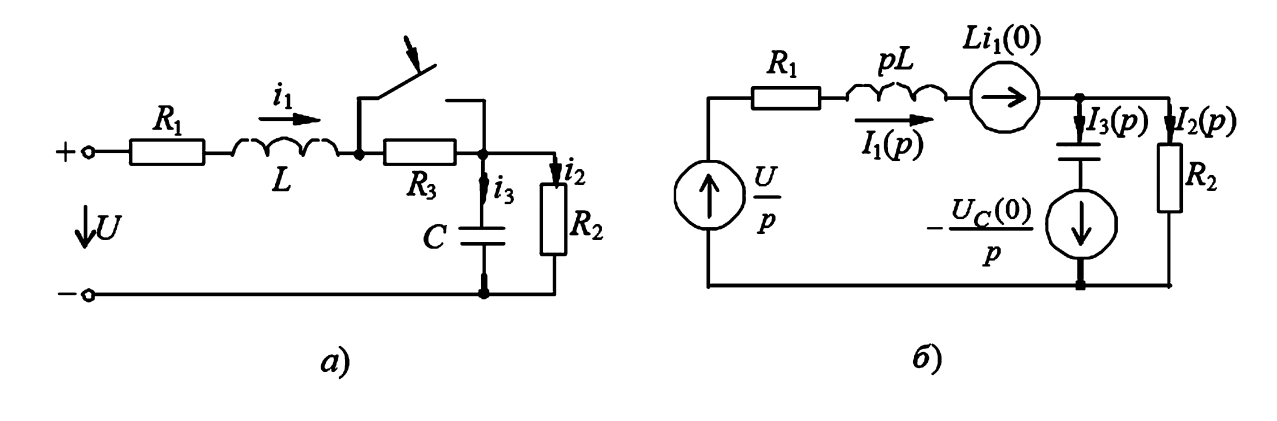
а — исходная схема (подразумевается, что при t>0); б — операторная схема замещения с учетом начальных условий.

На рисунке 1б показаны внутренние ЭДС, учитывающие начальные условия. Важно обратить внимание на их направления: ЭДС от начального тока $Li_1(0)$ направлена согласно с током $I_1(p)$, а ЭДС от начального заряда $\frac{U_C(0)}{p}$ направлена против тока $I_3(p)$ (или согласно с $I_2(p)$ в зависимости от выбора контура).

Переход от изображений к оригиналам (Формула разложения)

После решения алгебраической системы мы получаем изображение искомой величины в виде дробно-рациональной функции:

$$F(p) = \frac{N(p)}{M(p)}$$

где $N(p)$ и $M(p)$ — полиномы, причем степень $N(p)$ обычно меньше степени $M(p)$.

Для нахождения оригинала $f(t)$ используется вторая теорема разложения (формула Хевисайда). Если уравнение $M(p) = 0$ имеет $m$ простых (некратных) корней $p_1, p_2, …, p_m$, то оригинал находится как:

$$f(t) = \sum_{k=1}^{m} \frac{N(p_k)}{M'(p_k)} e^{p_k t}$$

где $M'(p)$ — производная знаменателя $\frac{dM(p)}{dp}$.

Если один из корней равен нулю ($p_k = 0$), соответствующее слагаемое $\frac{N(0)}{M'(0)}$ представляет собой принужденную (установившуюся) составляющую, обусловленную постоянной ЭДС.
Если среди корней есть пара комплексно-сопряженных $p_{1,2} = -\delta \pm j\omega$, то сумма двух соответствующих слагаемых в формуле разложения дает затухающую гармоническую функцию:
$$f_{1,2}(t) = 2 \text{Re}\left[ \frac{N(p_1)}{M'(p_1)} e^{p_1 t} \right] = A e^{-\delta t} \cos(\omega t + \phi)$$

Пример 1

Определить ток $i_1(t)$ при переходном процессе в схеме (рис. 1а), если $U = 125 \text{ В}$, $R_1 = 50 \text{ Ом}$, $R_2 = 200 \text{ Ом}$, $L = 10 \text{ мГн}$, $C = 5 \text{ мкФ}$. (Примечание: значение $R_3 = 250 \text{ Ом}$ из оригинального текста используется только для расчета начальных условий, но отсутствует в схеме переходного процесса).

Примечание к задаче: В данном примере существует несоответствие между расчетом начальных условий (где используется $R_3$) и схемой переходного процесса (рис. 1а, где $R_3$ отсутствует). Мы будем следовать логике примера, принимая начальные условия как заданные.

Решение

1. Определение начальных условий (до коммутации, $t < 0$)

Предполагается, что до коммутации цепь находилась в установившемся режиме. По данным из оригинального текста, ток $i_1$ (протекающий через $L$) и напряжение $u_C$ определены с учетом $R_3$:

$i_1(0-) = i_L(0-) = \frac{U}{R_1 + R_2 + R_3} = \frac{125}{50 + 200 + 250} = \frac{125}{500} = 0.25 \text{ А}$

$u_C(0-) = i_1(0-) \cdot R_2 = 0.25 \cdot 200 = 50 \text{ В}$ (Предполагается, что C и R2 были соединены специфическим образом до $t=0$).

Согласно первому закону коммутации, $i_L(0+) = i_L(0-) = 0.25 \text{ А}$.
Согласно второму закону коммутации, $u_C(0+) = u_C(0-) = 50 \text{ В}$.

2. Составление операторной схемы замещения (при $t > 0$)

Начертим операторную схему замещения (рис. 1б) для схемы, получившейся после коммутации (рис. 1а). В ней, кроме внешнего источника $U(p) = U/p$, появятся внутренние источники ЭДС, учитывающие начальные условия: $Li_1(0)$ и $u_C(0)/p$.

3. Составление уравнений по законам Кирхгофа

Составим систему уравнений для операторной схемы на рис. 1б, используя метод узловых потенциалов или метод контурных токов. В тексте примера используется система из трех уравнений (по токам $I_1$, $I_2$, $I_3$):

$$
\begin{cases}
I_1(p) — I_2(p) — I_3(p) = 0 \\
R_1 I_1(p) + pLI_1(p) + R_2 I_2(p) = \frac{U}{p} + Li_1(0) \\
R_2 I_2(p) — \frac{1}{pC} I_3(p) = -\frac{u_C(0)}{p}
\end{cases}
$$

Решая эту систему уравнений относительно $I_1(p)$, получаем:

$$I_1(p) = \frac{ \frac{U}{p} \left(R_2 + \frac{1}{pC} \right) + Li_1(0)\left(R_2 + \frac{1}{pC}\right) — R_2 \frac{u_C(0)}{p} }{ (R_1+pL)\left(R_2 + \frac{1}{pC}\right) + R_2 \frac{1}{pC} }$$

После алгебраических преобразований и подстановки числовых значений ( $L=0.01$, $C=5 \cdot 10^{-6}$, $i_1(0)=0.25$, $u_C(0)=50$, $R_1=50$, $R_2=200$, $U=125$ ):

$$I_1(p) = \frac{N(p)}{M(p)} = \frac{p^2(0.06) + p(250) + 10 \cdot 10^6}{p^3(2.5 \cdot 10^{-6}) + p^2(0.0775) + p(12500)}$$

Для упрощения анализа из M(p) можно вынести p:

$$I_1(p) = \frac{p^2(0.06) + p(250) + 10 \cdot 10^6}{p [p^2(2.5 \cdot 10^{-6}) + p(0.0775) + 12500]}$$

4. Нахождение оригинала $i_1(t)$

Для нахождения $i_1(t)$ применим формулу разложения. Для этого найдем корни знаменателя $M(p) = 0$:

$p_1 = 0$

И корни квадратного уравнения $p^2(2.5 \cdot 10^{-6}) + p(0.0775) + 12500 = 0$. Решая его, получаем комплексно-сопряженные корни (данные из примера):

$p_{2,3} = -3000 \pm j4000 \text{ c}^{-1}$

Оригинал тока $i_1(t)$ будет состоять из принужденной составляющей (от корня $p_1=0$) и свободной составляющей (от корней $p_{2,3}$):

$$i_1(t) = i_{\text{прин}} + i_{\text{своб}}(t)$$

Принужденная составляющая (установившийся режим):

$N(p) = U(R_2 pC + 1) + pC Li(0)(R_2 pC + 1) — R_2 u_C(0) pC$
$N(p) = 125(200 \cdot 5 \cdot 10^{-6} p + 1) + … \approx 125$ при $p \to 0$.
$M(p) = p[(R_1+pL)(R_2 pC + 1) + R_2]$
$\lim_{p \to 0} [p I_1(p)] = \frac{N(0)}{M'(0)} = \frac{125}{R_1 + R_2} = \frac{125}{50+200} = 0.5 \text{ A}$.
$i_{\text{прин}} = 0.5 \text{ А}$.

Свободная составляющая (колебательный процесс):

Определяется корнями $p_{2,3}$. Расчет по формуле разложения для комплексно-сопряженных корней дает:

$$i_{\text{своб}}(t) = 2 \text{Re}\left[ \frac{N(p_2)}{M'(p_2)} e^{p_2 t} \right] \approx 1.4 e^{-3000t} \cos(4000t — 100.2^\circ)$$

Полный ток:

$$i_1(t) = 0.5 + 1.4 e^{-3000t} \sin(4000t — 10.2^\circ) \text{ А}$$

Передаточные функции и временные характеристики

Передаточная функция

Передаточной функцией $K(p)$ четырехполюсника (линейной системы) на комплексной частоте $p$ называют отношение изображения выходного сигнала (реакции) к изображению входного сигнала (воздействия) при нулевых начальных условиях.

Чаще всего ее определяют как отношение изображения выходного напряжения $U_2(p)$ ко входному $U_1(p)$:

$$K(p) = \frac{U_2(p)}{U_1(p)}$$

Из этого уравнения следует, что изображение реакции равно произведению изображения воздействия на передаточную функцию:

$$U_2(p) = K(p) U_1(p)$$

Передаточная функция $K(p)$ полностью описывает динамические свойства системы и зависит только от ее схемы и параметров элементов, но не от входного сигнала.

Например, для RL-цепочки (рис. 2), если входным напряжением считать $U_1$, а выходным — напряжение на резисторе $U_2$, то передаточная функция будет:

$$K(p) = \frac{U_R(p)}{U_{in}(p)} = \frac{I(p) \cdot R}{I(p) \cdot (R + pL)} = \frac{R}{R + pL}$$

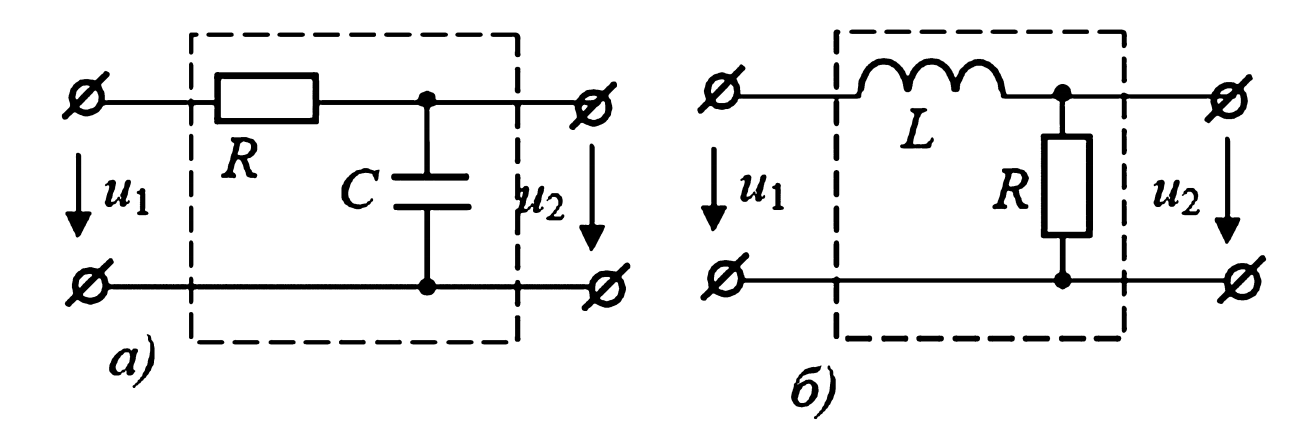
Рисунок 2 — Схема электрической RL-цепи (четырехполюсник).

Если несколько четырехполюсников соединены каскадно (выход одного подключен ко входу следующего) и они не нагружают друг друга, то общая передаточная функция каскада равна произведению их передаточных функций (рис. 3):

$$K(p) = K_1(p) K_2(p) K_3(p)$$

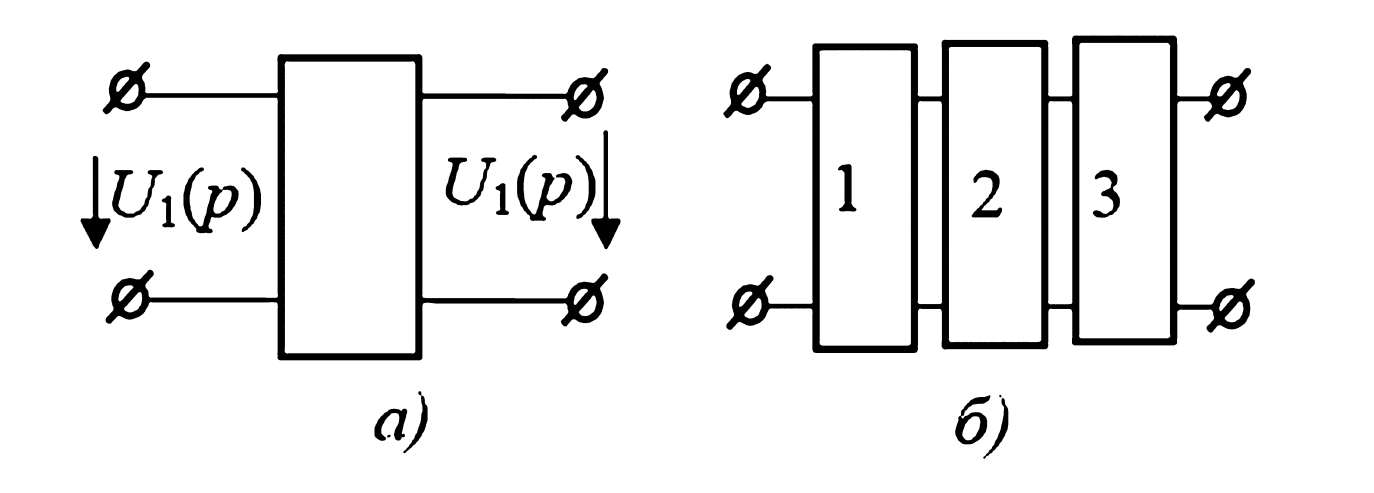
Рисунок 3 — Схемы четырехполюсников: а — простой; б — каскадное соединение.

Если в передаточной функции $K(p)$ заменить комплексную частоту $p$ на $j\omega$, мы получим комплексную частотную характеристику (КЧХ) $K(j\omega)$, используемую для анализа установившихся синусоидальных режимов.

Временные характеристики

Помимо передаточной функции, систему описывают ее временные характеристики — это реакции системы на типовые входные воздействия при нулевых начальных условиях.

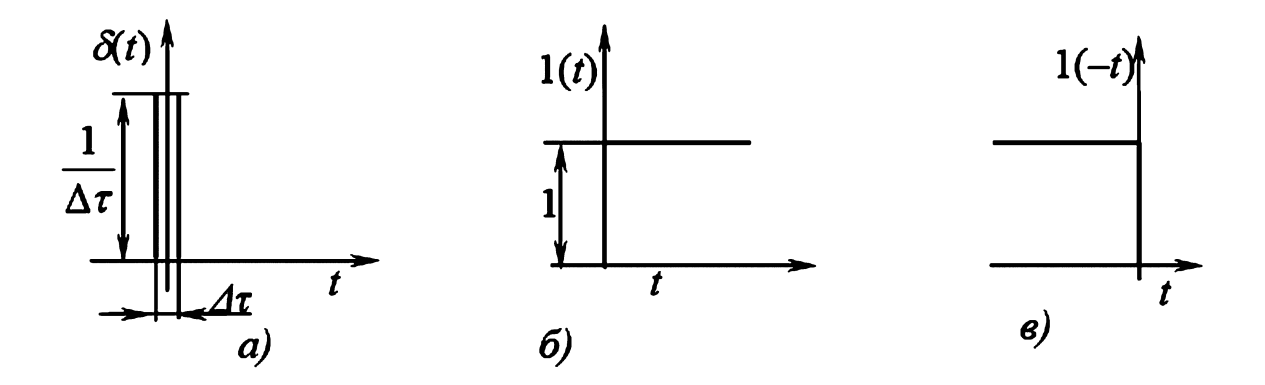
Рисунок 4 — Специальные функции: а — единичный импульс $\delta(t)$; б — единичная ступенька $1(t)$; в — «обратная» ступенька $1(-t)$.

Переходная характеристика $h(t)$:Это реакция системы (например, выходное напряжение $u_2(t)$) на единичное ступенчатое воздействие $u_1(t) = 1(t)$ (рис. 4б). Функция $1(t)$ (функция Хевисайда) равна 0 при $t < 0$ и 1 при $t > 0$.
Изображение единичной ступеньки: $1(t) \leftrightarrow 1/p$.
Тогда изображение переходной характеристики $H(p)$ связано с передаточной функцией $K(p)$ следующим образом:
$$H(p) = K(p) \cdot U_1(p) = K(p) \cdot \frac{1}{p}$$
Отсюда:
$$K(p) = p H(p)$$
И, соответственно, оригинал $h(t)$ можно найти из $K(p)$:
$$h(t) \leftrightarrow \frac{K(p)}{p}$$
Импульсная переходная характеристика $h_\delta(t)$ (или $g(t)$):Это реакция системы на единичный импульс $\delta(t)$ (дельта-функция Дирака, рис. 4а). $\delta(t)$ — это бесконечно короткий импульс бесконечно большой амплитуды, площадь которого равна 1. Его размерность — секунда в минус первой степени (1/c).
Изображение дельта-функции: $\delta(t) \leftrightarrow 1$.
Тогда изображение импульсной характеристики $H_\delta(p)$ равно:
$$H_\delta(p) = K(p) \cdot U_1(p) = K(p) \cdot 1 = K(p)$$Вывод: Импульсная переходная характеристика $h_\delta(t)$ является оригиналом для передаточной функции $K(p)$.$$h_\delta(t) \leftrightarrow K(p)$$Существует также связь между переходной и импульсной характеристиками. Так как $K(p) = p H(p)$ и $H(p) \leftrightarrow h(t)$, то с учетом начального $h(0)$ имеем:
$$K(p) \leftrightarrow \frac{dh(t)}{dt} + h(0)\delta(t)$$
Таким образом, импульсная характеристика $h_\delta(t)$ связана с производной от переходной характеристики $h(t)$:
$$h_\delta(t) = \frac{dh(t)}{dt} + h(0)\delta(t)$$
Если $h(0)=0$ (система не реагирует мгновенно), то $h_\delta(t) = h'(t)$.

Знание импульсной характеристики $h_\delta(t)$ позволяет найти реакцию $y(t)$ системы на любое входное воздействие $x(t)$ через интеграл Дюамеля (интеграл свертки):

$$y(t) = \int_{0}^{t} x(\tau) h_\delta(t — \tau) d\tau$$

Преимущества и недостатки операторного метода

Преимущества

Алгебраизация: Заменяет решение систем дифференциальных уравнений решением систем алгебраических уравнений, что значительно проще.
Учет начальных условий: Начальные условия (ток в L, напряжение на C) вводятся непосредственно в алгебраические уравнения на начальном этапе расчета, а не на конечном этапе, как в классическом методе.
Универсальность: Метод одинаково хорошо описывает как свободные, так и принужденные составляющие переходного процесса. Нет необходимости разделять решение.
Анализ систем: Понятие передаточной функции, вытекающее из операторного метода, является основой современной теории автоматического управления (ТАУ) для анализа устойчивости, качества и динамики систем.
Работа с разрывными функциями: Позволяет легко анализировать цепи при воздействии импульсных, ступенчатых и других разрывных сигналов.

Недостатки

Абстрактность: Метод оперирует комплексной частотой $p$, что менее наглядно, чем физические величины во временной области.
Сложность обратного преобразования: Нахождение корней знаменателя $M(p)$ (особенно для цепей высокого порядка) и применение теоремы разложения может быть трудоемкой математической задачей.
Ограничение: В своем базовом виде метод применим только к линейным цепям с постоянными параметрами (R, L, C — константы).

Сравнение операторного и классического методов

Критерий	Классический метод	Операторный метод
Математический аппарат	Решение линейных дифференциальных уравнений (ЛДУ).	Интегральное преобразование Лапласа, алгебра.
Поиск решения	Раздельный поиск: $f(t) = f_{\text{прин}}(t) + f_{\text{своб}}(t)$.	Единый поиск полного решения $F(p)$ и затем $f(t)$.
Начальные условия	Используются в самом конце для нахождения постоянных интегрирования из $f(t)$ и $f'(t)$.	Вводятся в самом начале при составлении операторных уравнений.
Сложность при не-нулевых Н.У.	Высокая. Нахождение частного решения для ДУ становится сложным.	Низкая. Начальные условия просто добавляются как источники ЭДС/тока.
Входные воздействия	Трудоемко для разрывных и импульсных функций (метод Дюамеля).	Легко, т.к. у всех стандартных воздействий есть простые изображения.
Применимость	Линейные и нелинейные цепи.	Строго линейные цепи с постоянными параметрами.

Интересные факты по теме

Имя «Лаплас» было не первым. Оливер Хевисайд, британский инженер, разработал свой «операционный исчисление» для тех же целей, но не смог дать ему строгое математическое обоснование. Математики того времени критиковали его методы, хотя они и давали верные ответы.
Преобразование Лапласа «старше» Хевисайда. Пьер-Симон Лаплас разработал математическую основу преобразования в 1780-х годах для работы с теорией вероятностей, задолго до появления электротехники.
Связь с Фурье. Преобразование Лапласа является обобщением преобразования Фурье. Если в $p = \sigma + j\omega$ положить $\sigma = 0$, то (при определенных условиях) преобразование Лапласа сводится к преобразованию Фурье ($p = j\omega$).
Что такое «p»? Комплексная частота $p = \sigma + j\omega$ имеет глубокий физический смысл. $\omega$ — это привычная нам угловая частота (колебания), а $\sigma$ — это коэффициент затухания (или нарастания) экспоненты.
Основа ТАУ. Вся современная теория автоматического управления (ТАУ) построена на передаточных функциях $K(p)$. Анализируя нули и полюсы (корни числителя и знаменателя) $K(p)$, инженеры судят об устойчивости систем (например, автопилотов или регуляторов).
Интеграл Дюамеля. Этот интеграл, который в операторном методе выглядит как простое умножение $Y(p) = K(p)X(p)$, во временной области называется «сверткой» и показывает, как система «помнит» все прошлые воздействия.
Метод и ГОСТы. Расчет переходных процессов необходим для обеспечения норм качества электроэнергии, например, по ГОСТ 32144-2013. Этот стандарт регламентирует допустимые отклонения напряжения и другие параметры, которые «портятся» именно во время переходных процессов.

Часто задаваемые вопросы (FAQ)

1. Что такое «оригинал» и «изображение»?

Оригинал — это функция времени, описывающая физический процесс (например, $u(t)$ — напряжение). Изображение — это математическое представление этой функции в области комплексной частоты, полученное с помощью преобразования Лапласа (например, $U(p)$).

2. Зачем вообще переходить в «область p», если потом все равно возвращаться?

Потому что в «области p» (области изображений) задача неизмеримо проще. Решение сложного дифференциального уравнения заменяется на решение простого алгебраического уравнения (как в 7 классе). Трудности перехода «туда» и «обратно» окупаются простотой решения в «области p».

3. В чем разница между операторным методом и методом комплексных амплитуд?

Метод комплексных амплитуд (МКА) — это частный случай операторного метода. МКА работает только для синусоидальных сигналов и только для установившегося (принужденного) режима. Операторный метод работает для сигналов любой формы (ступенька, импульс, экспонента, синус) и описывает весь процесс (и свободный, и принужденный), то есть переходной процесс.

4. Что такое «нулевые начальные условия»?

Это означает, что до начала воздействия (до $t=0$) в цепи не было накоплено энергии: все токи через индуктивности и все напряжения на емкостях были равны нулю. Если они не равны нулю (ненулевые начальные условия), их учитывают как дополнительные источники ЭДС в операторной схеме.

5. Что такое передаточная функция K(p)?

Это «паспорт» системы. Он показывает, как система преобразует входной сигнал в выходной. Если $K(p) = 1/(p+1)$, это значит, что система является инерционной (фильтром низких частот). Зная $K(p)$, можно предсказать реакцию системы на любое воздействие, не зная ее внутренней схемы.

6. Можно ли использовать операторный метод для нелинейных цепей (например, с диодами)?

Нет. Стандартное преобразование Лапласа и операторный метод основаны на принципе суперпозиции, который работает только в линейных системах. Для анализа нелинейных цепей используют другие методы, например, численное моделирование или классический метод (составление нелинейных ДУ).

7. Что такое «полюсы» и «нули» передаточной функции?

Передаточная функция — это дробь $K(p) = N(p) / M(p)$. Нули — это корни числителя (значения $p$, при которых $N(p)=0$). Полюсы — это корни знаменателя (значения $p$, при которых $M(p)=0$). Полюсы (корни $M(p)$) определяют собственные (свободные) колебания в системе и ее устойчивость. Если хоть один полюс имеет положительную реальную часть, система неустойчива.

Заключение

Операторный метод является фундаментальным инструментом в арсенале современного инженера-электротехника. Его способность сводить сложные интегро-дифференциальные уравнения к алгебраическим задачам не только упрощает расчеты, но и обеспечивает более глубокое понимание динамики системы. Владение преобразованием Лапласа и понятием передаточной функции открывает дорогу к анализу сложных систем управления, фильтрации сигналов и обеспечению устойчивости и качества в электроэнергетических системах.

Нормативные документы

ГОСТ 32144-2013 — «Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения.» (Стандарт определяет параметры, на которые влияют переходные процессы).
ГОСТ Р 54130-2010 — «Качество электрической энергии. Термины и определения.» (Определяет терминологию, связанную с переходными процессами, провалами напряжения и т.д.).

№	Оригинал (функция времени) \(f(t)\)	Изображение (функция частоты) \(F(p)\)	Описание
1	\(\delta(t)\)	\(1\)	Дельта-функция (единичный импульс)
2	\(1(t)\)	\(\frac{1}{p}\)	Единичная ступенчатая функция (функция Хевисайда)
3	\(A\) (константа)	\(\frac{A}{p}\)	Постоянная величина (при \(t \ge 0\))
4	\(t\)	\(\frac{1}{p^2}\)	Линейно нарастающая функция
5	\(t^n\)	\(\frac{n!}{p^{n+1}}\)	Степенная функция
6	\(e^{-\alpha t}\)	\(\frac{1}{p + \alpha}\)	Затухающая экспонента
7	\(t e^{-\alpha t}\)	\(\frac{1}{(p + \alpha)^2}\)
8	\(\sin(\omega t)\)	\(\frac{\omega}{p^2 + \omega^2}\)	Синусоида
9	\(\cos(\omega t)\)	\(\frac{p}{p^2 + \omega^2}\)	Косинусоида
10	\(e^{-\alpha t} \sin(\omega t)\)	\(\frac{\omega}{(p + \alpha)^2 + \omega^2}\)	Затухающая синусоида
11	\(e^{-\alpha t} \cos(\omega t)\)	\(\frac{p + \alpha}{(p + \alpha)^2 + \omega^2}\)	Затухающая косинусоида

Операторный метод расчета переходных процессов в электрических цепях