Мощность в цепях переменного синусоидального тока

Содержание страницы

1. Мгновенная и активная мощность
2. Полная и реактивная мощность
3. Сравнительная таблица мощностей
4. Баланс мощностей
5. Преимущества и недостатки высокого коэффициента мощности
6. Интересные факты о мощности
7. FAQ: Часто задаваемые вопросы
Заключение

Мощность в цепях переменного тока — это физическая величина, характеризующая скорость передачи или преобразования электрической энергии. В отличие от постоянного тока, здесь мы сталкиваемся с тремя видами мощности: активной (полезной), реактивной (циркулирующей) и полной.

Историческая справка: Основы теории мощности переменного тока были заложены в конце XIX века. Ключевую роль сыграли работы Чарльза Штейнмеца, который в 1893 году предложил метод символического (комплексного) исчисления, что позволило значительно упростить расчеты цепей переменного тока и дало математическое обоснование понятию реактивной мощности.

1. Мгновенная и активная мощность

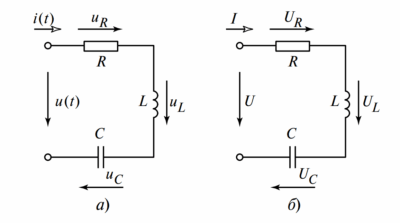
Рассмотрим классическую электрическую цепь, к которой приложено синусоидальное напряжение и через которую протекает ток. Эти величины описываются следующими выражениями:

u = U_m \sin(\omega t) $$ $$ i = I_m \sin(\omega t — \phi)

Где $ \phi $ — фазовый сдвиг между током и напряжением. Мгновенная мощность, поступающая в цепь, определяется как произведение мгновенных значений напряжения и тока:

p = ui = U_m I_m \sin(\omega t) \cdot \sin(\omega t — \phi)

Используя тригонометрические преобразования, это выражение можно привести к виду:

p = UI \cos(\phi) — UI \cos(2\omega t — \phi)

Здесь мы видим, что мгновенная мощность состоит из двух составляющих:

Постоянной величины: $ UI \cos(\phi) $.
Косинусоидальной (гармонической): $ UI \cos(2\omega t — \phi) $, которая колеблется с удвоенной частотой по сравнению с частотой напряжения и тока.

Среднее значение второй составляющей за время $ T $ (период), в течение которого она совершает два полных цикла изменений, равно нулю.

Обратите внимание на Рисунок 1: здесь четко показано, что за один период изменения тока $ T $ график мощности ( p(t) ) успевает совершить два полных колебания. При этом вся кривая мощности смещена вверх относительно оси времени на величину постоянной составляющей.

Поэтому активная мощность ( P ), поступающая в рассматриваемую цепь, определяется именно этим средним уровнем:

P = p_{cp} = UI \cos(\phi)

Рисунок 1. Временные диаграммы $ u(t), i(t), p(t) $.
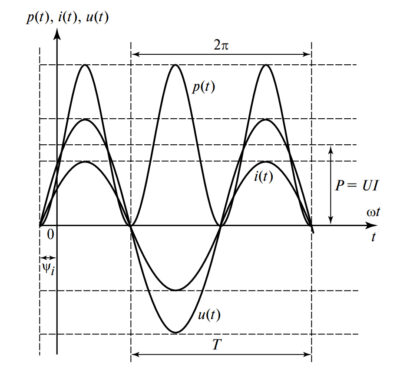
Наглядно видно, что период колебаний мощности в 2 раза меньше периода тока $ T $, а колебания происходят относительно среднего уровня $ P = UI $.

Коэффициент мощности

Множитель $ \cos(\phi) $ носит название коэффициента мощности (Power Factor). Активная мощность равна произведению действующих значений напряжения и тока, умноженному на этот коэффициент.

Важно: Чем ближе угол $ \phi $ к нулю, тем ближе $ \cos(\phi) $ к единице. Следовательно, тем большая активная мощность передается от источника к приемнику при заданных значениях напряжения $ U $ и тока $ I $. Повышение коэффициента мощности электротехнических устройств — это важнейшая инженерная и экономическая задача.

Единица измерения активной мощности: Ватт (Вт).

Физический смысл процессов

Мгновенная мощность колеблется с удвоенной угловой частотой относительно постоянной составляющей.

Рисунок 2а. Кривая мощности при нулевом сдвиге фаз (активная нагрузка, φ=0)

Рисунок 2б. Кривая мощности при сдвиге фаз (активно-реактивная нагрузка, φ≠0)

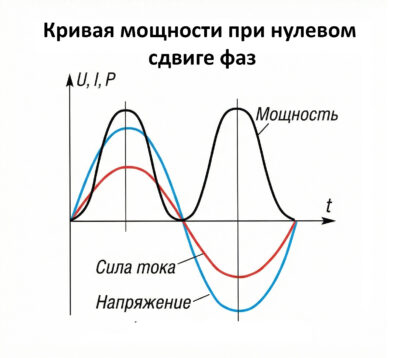
Обратите внимание на Рисунок 2а: здесь сдвиг фаз отсутствует (φ = 0). Напряжение и ток всегда имеют одинаковые знаки, поэтому кривая мощности целиком находится выше оси времени. Это значит, что энергия постоянно поступает от источника к потребителю.

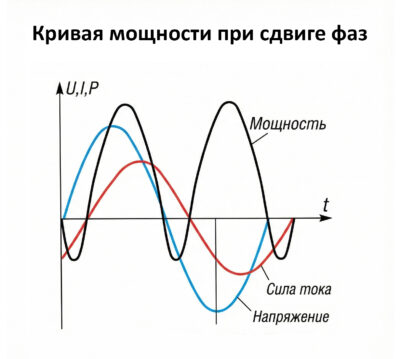
На Рисунке 2б показан случай сдвига фаз. В промежутки времени, когда напряжение и ток имеют одинаковые знаки, мгновенная мощность положительна (график выше оси). Энергия поступает от источника в приемник.

Однако, когда напряжение и ток имеют разные знаки (на графике 1б видны участки «провалов» ниже оси), мгновенная мощность становится отрицательной. В эти моменты энергия, запасенная в реактивных элементах (индуктивностях, емкостях), частично возвращается обратно к источнику.

2. Полная и реактивная мощность

Для полного описания энергетических процессов вводятся дополнительные понятия.

Полная мощность

Величина, равная произведению действующих значений тока и напряжения цепи, называется полной мощностью. Это предельная мощность, которую может выдать источник при чисто активной нагрузке.

$$ S = UI $$

Единица измерения: Вольт-ампер (В·А).

Реактивная мощность

При расчетах электротехнических цепей пользуются понятием реактивной мощности, характеризующей энергию, которой обмениваются генератор и приемник (индуктивность и емкость). Она вычисляется по формуле:

Q = UI \sin(\phi)

Эта мощность выражается в единицах, называемых вольт-амперами реактивными (вар).

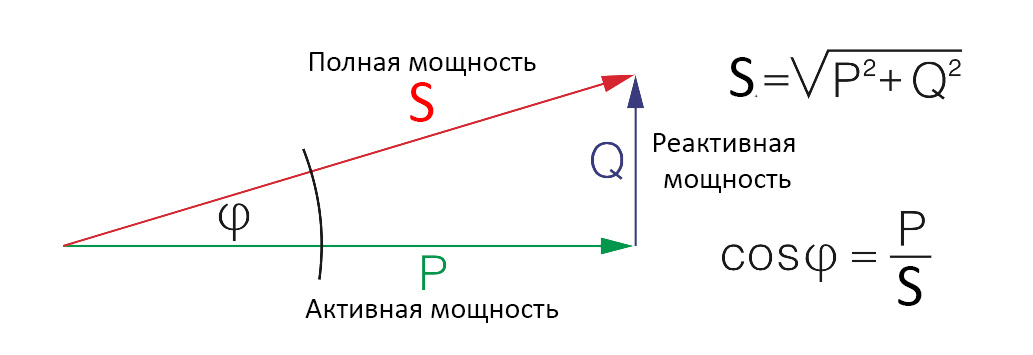
Треугольник мощностей

Полная мощность определяется как геометрическая сумма активной и реактивной мощностей. Мощности (полная, активная и реактивная) образуют так называемый треугольник мощностей, геометрически подобный треугольнику сопротивлений.

S = \sqrt{P^2 + Q^2}

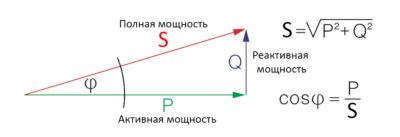
Рисунок 3. Треугольник мощностей. Катет P — активная мощность, катет Q — реактивная мощность, гипотенуза S — полная мощность. Угол φ соответствует сдвигу фаз.

Также рассматривается комплексная мощность $ \tilde{S} $, определяемая выражением:
$$ \tilde{S} = P + jQ $$
Единицей комплексной мощности, как и полной, является вольт-ампер (В·А).

3. Сравнительная таблица мощностей

Тип мощности	Обозначение	Формула	Единица (СИ)	Физический смысл
Активная	$ P $	$ UI \cos \phi $	Ватт (Вт)	Безвозвратное преобразование энергии (тепло, свет, механика).
Реактивная	$ Q $	$ UI \sin \phi $	Вар (вар)	Энергия, циркулирующая между источником и реактивными элементами (L, C).
Полная	$ S $	$ UI $ или $ \sqrt{P^2+Q^2} $	Вольт-ампер (В·А)	Максимальная нагрузка, на которую рассчитывается электрооборудование.

4. Баланс мощностей

Баланс мощностей применяется для проверки правильности решения электротехнических задач и является прямым следствием закона сохранения энергии в электрических цепях.

Сущность баланса: Мощность, отдаваемая в цепь источниками энергии переменного тока, полностью расходуется её элементами. Активная составляющая потребляется резисторами, а реактивная циркулирует в реактивных элементах.

Расчет комплексной мощности источника

Комплекс полной мощности, отдаваемой в цепь источником, определяется выражением (здесь учитываются источники ЭДС и тока):

\tilde{S}_{u} = \dot{U} \cdot \dot{I}^*

Где:

$ \dot{U} $ — комплексное значение разности потенциалов на зажимах источника (напряжение).
$ \dot{I}^* $ — сопряженное комплексное значение тока, текущего от источника в цепь.

Пусть комплексы напряжения и тока записаны в показательной форме:

\dot{U} = U e^{j\psi_u} $$ $$ \dot{I} = I e^{j\psi_i} \quad \Rightarrow \quad \dot{I}^* = I e^{-j\psi_i}

Подставим эти значения в формулу мощности:

\tilde{S}_{u} = U e^{j\psi_u} \cdot I e^{-j\psi_i} = UI e^{j(\psi_u — \psi_i)} = S_{u} e^{j\phi}

Здесь $ \phi = \psi_u — \psi_i $ — сдвиг фаз между напряжением и током.

Для практического расчета баланса уравнение приводят к алгебраической форме, используя формулу Эйлера:

\tilde{S}_{u} = S_{u} (\cos \phi + j \sin \phi) = P_{u} + jQ_{u}

Так определяют полную $ S_{u} $, активную $ P_{u} $ и реактивную $ Q_{u} $ мощности, отдаваемые источником в сеть.

Методика проверки баланса

При расчете баланса учитывается, что все резисторы потребляют активную мощность, а реактивные элементы — реактивную:

P_{n} = I^2 R $$ $$ Q_{n} = I^2 X_L — I^2 X_C

Алгоритм проверки:

Находят комплексное значение полной мощности для всех источников в цепь, суммируют их активные $ \sum P_u $ и реактивные $ \sum Q_u $ составляющие.
По найденным токам вычисляют мощность приемников:
- $ P_R = R I^2 $ (на резисторах);
- $ Q_L = X_L I^2 $ (в индуктивностях, $ Q_L > 0 $);
- $ Q_C = X_C I^2 $ (в емкостях, $ Q_C < 0 $).
Баланс сходится, если выполняются равенства:
$$ \sum P_u = \sum P_n \quad \text{и} \quad \sum Q_u = \sum Q_n $$

5. Преимущества и недостатки высокого коэффициента мощности

Поскольку управление мощностью сводится к управлению $ \cos \phi $, рассмотрим плюсы и минусы поддержания его высокого значения (близкого к 1).

Аспект	Описание
Преимущества (высокий \( \cos \phi \))	Снижение потерь электроэнергии в линиях передачи (меньше нагрев проводов). Уменьшение падения напряжения в сети. Возможность использования трансформаторов и генераторов меньшей габаритной мощности при той же полезной нагрузке. Снижение затрат на оплату электроэнергии (отсутствие штрафов за реактив).
Недостатки/Сложности	Необходимость установки компенсирующих устройств (конденсаторных батарей, статических компенсаторов). Дополнительные капитальные затраты на обслуживание оборудования компенсации. Риск перекомпенсации (емкостной характер сети), что может привести к повышению напряжения в ночное время.

Аспект

Описание

Преимущества (высокий $ \cos \phi $)

Снижение потерь электроэнергии в линиях передачи (меньше нагрев проводов).
Уменьшение падения напряжения в сети.
Возможность использования трансформаторов и генераторов меньшей габаритной мощности при той же полезной нагрузке.
Снижение затрат на оплату электроэнергии (отсутствие штрафов за реактив).

Недостатки/Сложности

Необходимость установки компенсирующих устройств (конденсаторных батарей, статических компенсаторов).
Дополнительные капитальные затраты на обслуживание оборудования компенсации.
Риск перекомпенсации (емкостной характер сети), что может привести к повышению напряжения в ночное время.

Рисунок 4. Промышленная автоматическая конденсаторная установка (УКРМ) компенсации реактивной мощности. Оборудование используется для генерации реактивной мощности (Q) непосредственно у потребителя, что позволяет повысить общий коэффициент мощности ($ \cos \phi $) предприятия.

6. Интересные факты о мощности

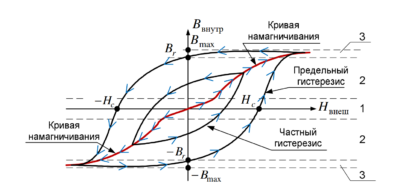
МАГНИТНЫЕ ПОЛЯ. Реактивная мощность не совершает полезной работы, но без неё невозможна работа трансформаторов и асинхронных двигателей, так как она создает необходимые магнитные поля.
НЕДОГРУЗКА ДВИГАТЕЛЕЙ. В промышленных сетях основной причиной низкого коэффициента мощности являются недогруженные асинхронные двигатели.
ИСТОРИЯ ТЕРМИНА. Термин «Вар» (вольт-ампер реактивный) был принят Международной электротехнической комиссией (IEC) в Стокгольме в 1930 году.
БЫТОВОЙ УЧЕТ. Обычные бытовые счетчики учитывают только активную мощность (кВт·ч). Реактивная мощность в квартирах обычно не тарифицируется.
ЕМКОСТЬ ЛИНИЙ. При передаче энергии на большие расстояния высоковольтные линии электропередач сами генерируют реактивную мощность из-за емкости между проводами и землей.
МАРКИРОВКА ОБОРУДОВАНИЯ. Полная мощность $ S $ часто указывается на шильдиках генераторов и трансформаторов, так как их нагрев зависит от полного тока, а не только от его активной составляющей.
МАТЕМАТИЧЕСКАЯ ОСНОВА. «Треугольник мощностей» — это мнемоническое правило, но математически оно справедливо, потому что векторы тока и напряжения в комплексной плоскости подчиняются правилам векторной алгебры.

7. FAQ: Часто задаваемые вопросы

Вопрос 1: Почему в формуле комплексной мощности берется сопряженный ток $ \dot{I}^* $?

Это необходимо для того, чтобы мнимая часть комплексной мощности $ Q $ соответствовала разности фаз $ \phi = \psi_u — \psi_i $. Если умножить просто на $ \dot{I} $, мы получим фазу $ \psi_u + \psi_i $, которая не имеет физического смысла в контексте мощности.

Вопрос 2: Может ли активная мощность быть отрицательной?

Да, если направление потока энергии меняется на противоположное (например, от нагрузки к источнику в режиме рекуперации), расчетная активная мощность будет иметь знак минус.

Вопрос 3: Почему емкостная мощность считается отрицательной?

Это условность, принятая в электротехнике. Индуктивный ток отстает от напряжения, а емкостной — опережает. Чтобы математически различать их вклад в баланс, принято считать $ Q_L > 0 $ (потребление), а $ Q_C < 0 $ (генерация реактивной мощности в сеть).

Вопрос 4: В чем разница между Ваттом и Вольт-Ампером?

Ватты (Вт) характеризуют реальную работу (тепло, движение). Вольт-Амперы (В·А) характеризуют полную нагрузку на провода и трансформатор. Если $ \cos \phi = 1 $, то 1 В·А = 1 Вт. Если $ \cos \phi < 1 $, то количество Ватт будет меньше, чем Вольт-Ампер.

Вопрос 5: Как проверить баланс, если он не сходится?

Частые ошибки: забыли сопряжение тока при расчете мощности источника; перепутали знаки индуктивной и емкостной мощности; арифметические ошибки в комплексных числах. Допустимая погрешность расчетов обычно составляет не более 1-2%.

Заключение

Понимание природы мощностей в цепях переменного тока — фундамент для любого инженера-электрика. Баланс мощностей служит главным критерием проверки корректности любых расчетов, а управление коэффициентом мощности позволяет значительно повысить эффективность энергосистем. Активная мощность дает нам полезную работу, реактивная обеспечивает функционирование электромагнитных полей, а полная определяет габариты и стоимость оборудования.

Нормативная база

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». (Основной документ, определяющий понятия активной, реактивной и полной мощности).
ГОСТ 32144-2013 «Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения».
ГОСТ IEC 60050-131-2015 «Международный электротехнический словарь. Часть 131. Теория цепей».

Мощность в цепях переменного синусоидального тока: теория и расчет