Методика расчета продольных параметров однофазных кабелей

Содержание страницы

1. Геометрия и конструкция кабеля: От физического объекта к расчетной модели
2. Математические модели расчета параметров: От точных формул к инженерным упрощениям
3. Математическая модель продольных сопротивлений
4. Влияние схем заземления экранов на параметры прямой и нулевой последовательности
5. Практические примеры и анализ результатов
6. Глубокий анализ индуктивности: Внутренние слагаемые и ошибки упрощения
7. Физика «Земли»: Параметры обратного провода и мифы о глубине $ D_{\text{з}} $
8. Сводная таблица сравнения методов заземления экранов
Заключение

Переход от воздушных линий электропередачи к кабельным (КЛ) — это глобальный тренд в развитии энергосистем мегаполисов и промышленных кластеров. Современные однофазные силовые кабели с изоляцией из сшитого полиэтилена (СПЭ) представляют собой сложные инженерные конструкции, электромагнитные процессы в которых существенно отличаются от процессов в воздушных линиях.

Если в середине XX века, когда доминировали кабели с бумажно-масляной изоляцией, расчеты часто велись по упрощенным эмпирическим формулам, то сегодня, с внедрением классов напряжения 110–500 кВ, требования к точности математического моделирования возросли многократно.

В отличие от трехжильного кабеля в общей оболочке, где магнитные потоки фаз частично компенсируют друг друга в пределах одного конструктива, однофазные кабели представляют собой независимые коаксиальные системы. Их электромагнитное взаимодействие определяется геометрией прокладки (треугольник или плоскость) и сложной схемой коммутации экранов.

Продольные параметры (активное сопротивление $R$ и индуктивность $L$) не являются константами, указанными в паспорте изделия. Это переменные величины, зависящие от:

Электромагнитного влияния соседних фаз (эффект близости).
Способа заземления экранов (возникновение контуров циркуляции токов).
Свойств окружающей среды (удельное сопротивление грунта).
Частоты протекающего тока (поверхностный эффект).

Данная статья представляет собой руководство по расчету собственных и взаимных параметров однофазных кабелей. Мы разберем физику процессов, влияние конструкции экрана на индуктивное и активное сопротивление, а также представим математическую модель, используемую службами релейной защиты и планирования режимов для расчета потерь, падений напряжения и токов короткого замыкания (КЗ).

1. Геометрия и конструкция кабеля: От физического объекта к расчетной модели

1.1. Конструктивные слои и их влияние на параметры

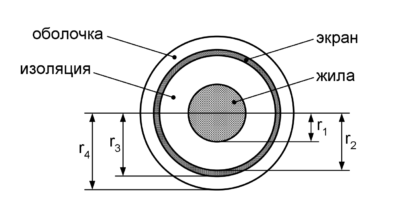
Для точного расчета погонных параметров необходимо преобразовать физическую конструкцию кабеля в геометрическую модель, описываемую набором радиусов. Рассмотрим однофазный кабель высокого напряжения. Это не просто проводник в изоляции, а сложная коаксиальная система.

Рис. 1. Конструкция однофазного силового кабеля с изоляцией из сшитого полиэтилена (СПЭ). Цифрами обозначены расчетные радиусы, соответствующие переходам между слоями.

Основные элементы конструкции, влияющие на расчет:

Токопроводящая жила (ТПЖ): Источник магнитного поля и основной путь протекания тока нагрузки.
Изоляция (СПЭ): Определяет емкостные параметры и диэлектрические потери.
Металлический экран: Ключевой элемент, влияющий на индуктивность и распределение токов КЗ. Экраны современных кабелей часто выполняются комбинированными (медные проволоки + медная лента).
Внешняя оболочка: Защищает от механических повреждений и влаги, определяет внешний теплообмен.

1.2. Система обозначений и базовые константы

В таблице ниже представлена унифицированная система обозначений, принятая в технической литературе и нормативной документации (включая стандарты МЭК и ГОСТ).

Таблица 1. Основные физические и геометрические величины

Величина	Обозначение	Размерность	Комментарий / Физический смысл
Внешний радиус токопроводящей жилы	$ r_1 $	м	Граница раздела «проводник – внутренняя полупроводящая лента/изоляция»
Внутренний радиус экрана	$ r_2 $	м	Определяет внешний диаметр основной изоляции
Внешний радиус экрана	$ r_3 $	м	Условная граница, учитывающая толщину проволок экрана
Внешний радиус кабеля	$ r_4 $	м	Габаритный размер по оболочке
Сечение жилы (номинальное)	$ F_{\text{ж}} $	мм²	Определяет пропускную способность по току
Сечение экрана (геометрическое)	$ F_{\text{э}} $	мм²	Важно для термической стойкости при КЗ
Относительная диэлектрическая проницаемость (основная изоляция)	$ \varepsilon_1 $	о.е.	Для сшитого полиэтилена $ \approx 2.3 — 2.5 $
Относительная диэлектрическая проницаемость (оболочка)	$ \varepsilon_2 $	о.е.	Для полиэтилена высокой плотности (HDPE)
Электрическая постоянная	$ \varepsilon_0 $	Ф/м	$ 8.85 \cdot 10^{-12} $
Магнитная постоянная	$ \mu_0 $	Гн/м	$ 4\pi \cdot 10^{-7} $
Удельное сопротивление жилы / экрана	$ \rho_{\text{ж}}, \rho_{\text{э}} $	Ом·м	Зависит от материала (Cu/Al) и температуры
Удельное сопротивление грунта	$ \rho_{\text{з}} $	Ом·м	Критично для расчетов нулевой последовательности

Важно! Производители кабелей (например, Prysmian, Nexans, заводы РФ) в каталогах обычно указывают номинальное сечение, а не точные геометрические радиусы. Использование номинального сечения для расчета радиуса по формуле круга $ r = \sqrt{S/\pi} $ дает ошибку, так как жила является многопроволочной и уплотненной.

1.3. Коэффициенты заполнения и реальная геометрия

Токопроводящая жила (ТПЖ) и экран не являются сплошными металлическими трубками. ТПЖ состоит из множества скрученных проволок, что приводит к наличию пустот между ними. Для учета этого фактора вводится понятие коэффициента заполнения ($ \gamma $).

F_K = \gamma_{\text{ж}} \cdot \pi \cdot r_1^2 $$ $$ F_{\text{э}} = \gamma_{\text{э}} \cdot \pi \cdot (r_3^2 — r_2^2)

Где:

$ \gamma_{\text{ж}} $ — коэффициент заполнения жилы. Для современных герметизированных жил он близок к 0.9–0.92, для сегментированных жил «Милликен» может быть еще выше.
$ \gamma_{\text{э}} $ — коэффициент заполнения экрана. Зависит от шага навивки проволок экрана и плотности их укладки.

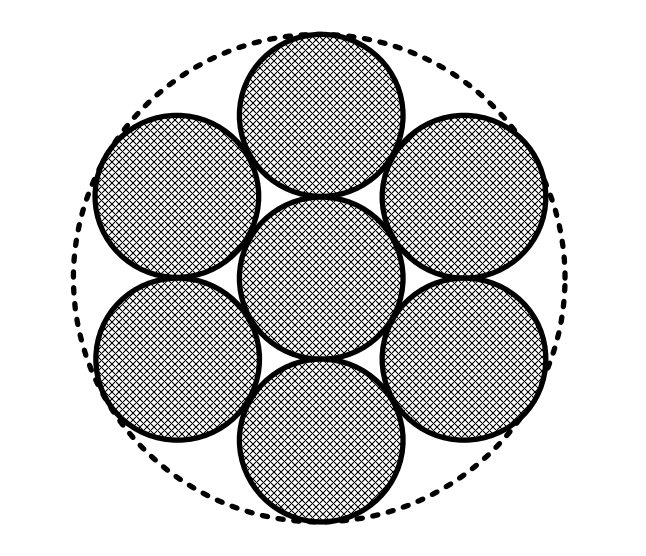
Рис. 2. Визуализация коэффициента заполнения. Сумма площадей отдельных проволок $ \sum f_i $ всегда меньше площади описывающего круга $ \pi R^2 $.

Аналогия: Представьте стакан, наполненный карандашами. Если смотреть сверху, карандаши занимают не всё пространство стакана — между ними есть воздух. «Коэффициент заполнения» показывает, какую часть объема реально занимает дерево и грифель, исключая воздух. В кабеле роль воздуха играют межпроволочные промежутки, часто заполненные водоблокирующими порошками или нитями.

Для практических расчетов, когда точные заводские данные недоступны, радиусы можно восстановить через сечения, принимая упрощение $ \gamma \approx 1 $ (с пониманием вносимой погрешности), или используя эмпирические формулы:

r_1 = \sqrt{\frac{F_K}{\pi \cdot \gamma_{\text{ж}}}} $$ $$ r_2 = r_1 + \Delta_{\text{жэ}} $$ $$ r_3 = \sqrt{r_2^2 + \frac{F_{\text{э}}}{\pi \cdot \gamma_{\text{э}}}} \approx r_2 + \frac{F_{\text{э}}}{2\pi r_2} \quad (\text{при } r_3 — r_2 \ll r_2) $$ $$ r_4 = r_3 + \Delta_{\text{ОБ}}

Толщины изоляции ($ \Delta_{\text{жэ}} $) и оболочки ($ \Delta_{\text{ОБ}} $) строго регламентируются стандартами. В Российской Федерации действует ГОСТ Р 55025-2012 «Кабели силовые с пластмассовой изоляцией на номинальное напряжение от 6 до 35 кВ включительно» и соответствующие стандарты МЭК для высоких напряжений.

Таблица 2. Ориентировочные толщины конструктивных элементов (усредненные данные)

Класс напряжения (кВ)	Толщина изоляции $ \Delta_{\text{жэ}} $ (мм)	Толщина оболочки $ \Delta_{\text{ОБ}} $ (мм)
6–10	4.0	2.5 – 3.0
20	5.5	2.5 – 3.0
35	8.0	2.5 – 3.5
110	15 – 16	3.5 – 4.5
220	23 – 27	4.5 – 5.0
330	28 – 32	5.0 – 6.0
500	32 – 35	6.0 – 7.5

2. Математические модели расчета параметров: От точных формул к инженерным упрощениям

Электромагнитное поле в кабельной линии зависит от частоты, свойств грунта и взаимного расположения фаз. Точный расчет требует решения уравнений Максвелла в цилиндрических координатах, что реализовано, например, в программных комплексах типа EMTP-ATP (Electromagnetic Transients Program).

Однако для инженерных задач (расчет уставок РЗА, оценка потерь) применение полных уравнений поля избыточно. Мы используем квазистационарное приближение, которое дает высокую точность на промышленной частоте (50/60 Гц).

2.1. Активное сопротивление (Resistive Component)

Активное сопротивление проводника на переменном токе всегда выше, чем на постоянном, из-за двух фундаментальных эффектов:

Поверхностный эффект (Skin effect): Ток вытесняется к поверхности проводника, уменьшая эффективное сечение.
Эффект близости (Proximity effect): Магнитное поле соседних проводников искажает распределение тока в рассматриваемом проводнике.

В упрощенной постановке мы пренебрегаем этими эффектами (считая их вклад малым для сечений до 150-240 мм² на частоте 50 Гц) и используем формулы постоянного тока:

R_{\text{ж}} = \rho_{\text{ж}} \frac{1}{F_K} \quad [\text{Ом/м}] $$ $$ R_{\text{э}} = \rho_{\text{э}} \frac{1}{F_{\text{э}}} \quad [\text{Ом/м}]

Примечание: Для жил больших сечений (630 мм² и выше) пренебрегать скин-эффектом недопустимо. Сопротивление может возрастать на 10-20%. В таких случаях применяют поправочные коэффициенты согласно стандарту IEC 60287.

Сопротивление земли как обратного провода на промышленной частоте определяется по формуле Карсона-Поллачека:

R_{\text{з}} = \frac{\pi^2 f \cdot 10^{-7}}{2} \approx 0.05 \text{ мОм/км (при 50 Гц)}

Заметьте, что активное сопротивление земли практически не зависит от её удельного сопротивления $ \rho_{\text{з}} $, а зависит только от частоты.

2.2. Индуктивность и взаимоиндукция (Inductive Parameters)

Индуктивные параметры определяются геометрией магнитного поля. Для системы «провод над землей» (или в земле) ключевым понятием является эквивалентная глубина возврата тока в земле ($ D_{\text{з}} $).

Земля не является идеальным проводником. Ток, уходящий в землю, распространяется в ней на большой глубине. Эквивалентная глубина $ D_{\text{з}} $ рассчитывается как:

D_{\text{з}} = 658 \sqrt{\frac{\rho_{\text{з}}}{f}} \quad [\text{м}]

Или, используя формулу из старых источников (приведенную в исходных данных):
$ D_{\text{з}} = 2.24 \sqrt{\frac{\rho_{\text{з}}}{\mu_0 \omega}} $.

Таблица 3. Основные формулы для расчета индуктивных и емкостных параметров

Параметр	Формула	Комментарий
Собственная индуктивность жилы	$ L_{\text{ж}} = \frac{\mu_0}{2\pi} \ln \left( \frac{D_{\text{з}}}{r_1} \right) $	Определяет полное потокосцепление петли «жила-земля»
Собственная индуктивность экрана	$ L_{\text{э}} = \frac{\mu_0}{2\pi} \ln \left( \frac{D_{\text{з}}}{r_2} \right) $	Аналогично для экрана, радиус берется средний ($ r_2 $)
Взаимоиндукция «жила – соседний кабель»	$ M_{\text{к}} = \frac{\mu_0}{2\pi} \ln \left( \frac{D_{\text{з}}}{S} \right) $	Зависит от расстояния $ S $ между фазами
Взаимоиндукция «жила – свой экран»	$ M_{\text{ж-э}} = \frac{\mu_0}{2\pi} \ln \left( \frac{D_{\text{з}}}{r_2} \right) $	В коаксиальной системе равна собственной индуктивности внешнего проводника (экрана)
Емкость «жила – экран»	$ C_{\text{жэ}} = \frac{2\pi \varepsilon_1 \varepsilon_0}{\ln(r_2/r_1)} $	Определяет зарядный ток кабеля

3. Математическая модель продольных сопротивлений

Для анализа режимов работы сети (например, расчета токов КЗ) физические параметры $ R, L, M $ объединяются в комплексные сопротивления $ Z $.

Ниже приведена система допущений, позволяющая упростить расчеты без существенной потери точности:

Расстояние между фазами $ S $ значительно больше радиуса кабеля ($ S \gg r_2 $).
При расположении фаз треугольником расстояния равны. При расположении в плоскости (частый случай прокладки в траншее) используется среднегеометрическое расстояние: $ S = \sqrt[3]{d \cdot d \cdot 2d} \approx 1.26 d $.
Толщина экрана мала по сравнению с радиусом, поэтому $ r_3 \approx r_2 $.
Токами смещения в земле пренебрегаем (на частоте 50 Гц земля — чисто резистивный проводник).

3.1. Комплексные сопротивления в матричной форме

Полное продольное сопротивление кабельной линии можно представить через собственные ($ Z_{\text{ж}}, Z_{\text{э}} $) и взаимные ($ Z_{\text{к}} $) импедансы.

Z_{\text{ж}} = R_{\text{з}} + R_{\text{ж}} + j\omega L_{\text{ж}} \quad \text{(Собственное сопротивление контура жила-земля)} $$ $$ Z_{\text{э}} = R_{\text{з}} + R_{\text{э}} + j\omega L_{\text{э}} \quad \text{(Собственное сопротивление контура экран-земля)} $$ $$ Z_{\text{к}} = R_{\text{з}} + j\omega M_{\text{к}} \quad \text{(Взаимное сопротивление между фазами)} $$ $$ Z_{\text{жэ}} = R_{\text{з}} + j\omega M_{\text{ж-э}} \quad \text{(Взаимное сопротивление жила-экран)}

Обратите внимание: слагаемое $ R_{\text{з}} $ (сопротивление земли) входит во все уравнения, так как земля является общим обратным проводом для всех контуров. Это фундаментальное свойство систем с землей.

3.2. Система уравнений падений напряжения

Связь между падениями напряжений вдоль линии ($ \Delta U $) и токами в жилах ($ I_{\text{ж}} $) и экранах ($ I_{\text{э}} $) описывается системой линейных уравнений. Для трехфазной группы однофазных кабелей это система 6-го порядка (3 жилы + 3 экрана).

Рассмотрим структуру уравнений для фазы А (аналогично для B и C):

\Delta U_{\text{жA}} = Z_{\text{ж}} I_{\text{жA}} + Z_{\text{жэ}} I_{\text{эA}} + Z_{\text{к}} (I_{\text{жB}} + I_{\text{эB}}) + Z_{\text{к}} (I_{\text{жC}} + I_{\text{эC}}) $$ $$ \Delta U_{\text{эA}} = Z_{\text{э}} I_{\text{эA}} + Z_{\text{жэ}} I_{\text{жA}} + Z_{\text{к}} (I_{\text{жB}} + I_{\text{эB}}) + Z_{\text{к}} (I_{\text{жC}} + I_{\text{эC}})

Физический смысл системы: Падение напряжения на жиле фазы А создается не только током этой жилы, но и:

Током, протекающим в экране «своей» фазы (через сильную магнитную связь $ Z_{\text{жэ}} $).
Токами жил и экранов соседних фаз B и C (через взаимную индукцию $ Z_{\text{к}} $).

3.3. Математическое ядро модели

Ниже приведена полная система уравнений, описывающая электромагнитное равновесие в трехфазной кабельной линии. Она учитывает не только падение напряжения в собственном проводнике, но и наведенные ЭДС от всех остальных пяти проводников системы (двух соседних жил и трех экранов).

$$ \left\{ \begin{aligned} \Delta \dot{U}_{\text{ж}A} &= \dot{Z}_{\text{ж}} \dot{I}_{\text{ж}A} + \dot{Z}_{\text{жэ}} \dot{I}_{\text{э}A} + \dot{Z}_{\text{к}} (\dot{I}_{\text{ж}B} + \dot{I}_{\text{э}B}) + \dot{Z}_{\text{к}} (\dot{I}_{\text{ж}C} + \dot{I}_{\text{э}C}) \\ \Delta \dot{U}_{\text{ж}B} &= \dot{Z}_{\text{ж}} \dot{I}_{\text{ж}B} + \dot{Z}_{\text{жэ}} \dot{I}_{\text{э}B} + \dot{Z}_{\text{к}} (\dot{I}_{\text{ж}A} + \dot{I}_{\text{э}A}) + \dot{Z}_{\text{к}} (\dot{I}_{\text{ж}C} + \dot{I}_{\text{э}C}) \\ \Delta \dot{U}_{\text{ж}C} &= \dot{Z}_{\text{ж}} \dot{I}_{\text{ж}C} + \dot{Z}_{\text{жэ}} \dot{I}_{\text{э}C} + \dot{Z}_{\text{к}} (\dot{I}_{\text{ж}A} + \dot{I}_{\text{э}A}) + \dot{Z}_{\text{к}} (\dot{I}_{\text{ж}B} + \dot{I}_{\text{э}B}) \\[1em] \Delta \dot{U}_{\text{э}A} &= \dot{Z}_{\text{э}} \dot{I}_{\text{э}A} + \dot{Z}_{\text{жэ}} \dot{I}_{\text{ж}A} + \dot{Z}_{\text{к}} (\dot{I}_{\text{ж}B} + \dot{I}_{\text{э}B}) + \dot{Z}_{\text{к}} (\dot{I}_{\text{ж}C} + \dot{I}_{\text{э}C}) \\ \Delta \dot{U}_{\text{э}B} &= \dot{Z}_{\text{э}} \dot{I}_{\text{э}B} + \dot{Z}_{\text{жэ}} \dot{I}_{\text{ж}B} + \dot{Z}_{\text{к}} (\dot{I}_{\text{ж}A} + \dot{I}_{\text{э}A}) + \dot{Z}_{\text{к}} (\dot{I}_{\text{ж}C} + \dot{I}_{\text{э}C}) \\ \Delta \dot{U}_{\text{э}C} &= \dot{Z}_{\text{э}} \dot{I}_{\text{э}C} + \dot{Z}_{\text{жэ}} \dot{I}_{\text{ж}C} + \dot{Z}_{\text{к}} (\dot{I}_{\text{ж}A} + \dot{I}_{\text{э}A}) + \dot{Z}_{\text{к}} (\dot{I}_{\text{ж}B} + \dot{I}_{\text{э}B}) \end{aligned} \right. $$ (1)

Формула (1). Полная система уравнений продольных падений напряжения. Обратите внимание: слагаемые с $ \dot{Z}_{\text{к}} $ описывают влияние соседних фаз, которое часто игнорируется в упрощенных расчетах, но критически важно для точного моделирования.

4. Влияние схем заземления экранов на параметры прямой и нулевой последовательности

В предыдущих разделах мы рассматривали общую физическую модель кабеля. Однако на практике кабель никогда не работает «сам по себе». Критическое влияние на его результирующее сопротивление (импеданс) оказывает схема соединения и заземления металлических экранов. Именно граничные условия на концах линии определяют, потечет ли ток по экрану, и если потечет — то какой величины и фазы.

Инженеры-проектировщики и специалисты служб релейной защиты (РЗА) оперируют понятиями симметричных составляющих (прямой, обратной и нулевой последовательности). Это математическая абстракция, позволяющая упростить расчет несимметричных режимов (например, коротких замыканий).

Теоретическая справка:

Прямая последовательность ($Z_1$): Характеризует нормальный режим работы. Токи в фазах равны и сдвинуты на 120°. Сумма токов равна нулю, ток в земле отсутствует.
Нулевая последовательность ($Z_0$): Характеризует режим однофазного замыкания на землю (ОЗЗ). Токи во всех трех фазах совпадают по фазе и величине. Весь суммарный ток ($3I_0$) возвращается через землю и экраны.

4.1. Граничные условия и математическая модель

Для перехода от общей системы уравнений к практическим формулам сопротивлений, необходимо наложить ограничения (граничные условия), зависящие от способа монтажа экранов (Таблица 4).

При выводе формул приняты следующие допущения:

Емкостными токами (поперечной проводимостью) пренебрегаем, так как рассматриваем продольные импедансы.
Переходными сопротивлениями в контактах заземления пренебрегаем (считаем заземление идеальным), однако в расчетах нулевой последовательности сопротивление контура заземления подстанции должно учитываться отдельно.
При наличии транспозиции экранов считается, что цикл транспозиции полный и длина участков идеально симметрична.

Таблица 4. Классификация режимов работы экранов

№	Схема заземления	Физический смысл граничных условий
1	Одностороннее заземление (Single Point Bonding)	Экран заземлен только в одном узле. Контур для протекания тока по экрану разомкнут. Ток в экране $ I_{\text{э}} = 0 $. На незаземленном конце наводится потенциал.
2	Двустороннее заземление (Solid Bonding)	Экран заземлен с обоих концов. Образуется замкнутый контур «экран-земля». В экране протекают циркулирующие токи, индуцированные током жилы.
3	Транспозиция экранов (Cross-Bonding)	Экраны разных фаз перекрестно соединяются в специальных узлах (коробках транспозиции). Векторная сумма наведенных ЭДС на длине цикла стремится к нулю, минимизируя токи в экранах.

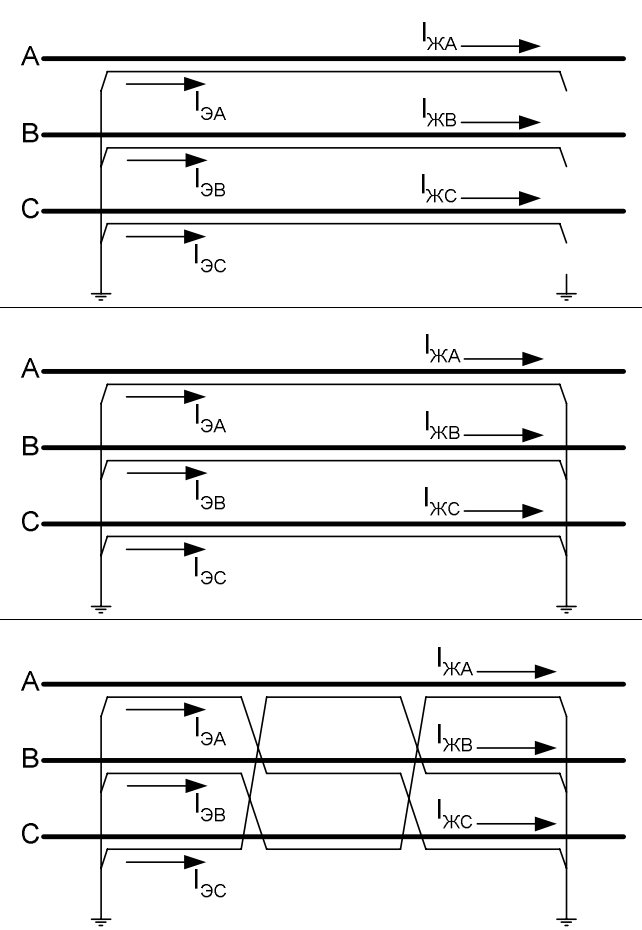
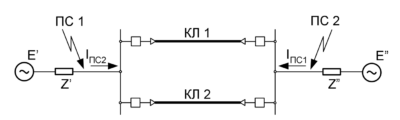
Рис. 3. Основные схемы соединения экранов силовых кабелей: 1) Одностороннее заземление с ограничителем перенапряжения (ОПН) на конце. 2) Глухое заземление с двух сторон. 3) Схема транспозиции (кросс-бондинга) с делением трассы на три участка.
Выбор схемы определяет не только потери, но и продольные сопротивления линии.

4.2. Дополнительные условия для метода симметричных составляющих

Чтобы получить итоговые формулы $Z_1$ и $Z_0$, мы решаем систему уравнений (1) при специфических условиях распределения токов в жилах.

Таблица 5. Условия токов для расчета последовательностей

Решаемая задача	Условия для токов в жилах	Комментарий
Расчет сопротивления прямой последовательности ($Z_1$)	$ I_{\text{жA}} + I_{\text{жB}} + I_{\text{жC}} = 0 $ $ I_{\text{эA}} + I_{\text{эB}} + I_{\text{эC}} = 0 $	Симметричная трехфазная система. Ток в земле отсутствует.
Расчет сопротивления нулевой последовательности ($Z_0$)	$ I_{\text{жA}} = I_{\text{жB}} = I_{\text{жC}} = I_0 $	Токи совпадают по фазе. Весь ток возвращается через землю и заземленные экраны.

4.3. Итоговые формулы для расчета параметров

В Таблице 6 представлены аналитические выражения, полученные в результате решения системы уравнений. Это «золотой стандарт» для расчета уставок релейной защиты кабельных линий.

Таблица 6. Формулы продольных погонных параметров (Ом/м)

Состояние экрана	Сопротивление прямой последовательности (\(Z_1\))	Сопротивление нулевой последовательности (\(Z_0\))
Одностороннее заземление (или транспозиция, см. прим.)	\( Z_1 = Z_{\text{ж}} — Z_{\text{к}} \) Примечание: Здесь экран не влияет на \(Z_1\), так как ток в нем равен нулю.	\( Z_0 = Z_{\text{ж}} + 2Z_{\text{к}} \) Примечание: Ток возвращается только через землю.
Двустороннее заземление (Solid Bonding)	$$ Z_1 = (Z_{\text{ж}} — Z_{\text{к}}) + \frac{(Z_{\text{к}} — Z_{\text{жэ}})^2}{Z_{\text{э}} — Z_{\text{к}}} $$ Второе слагаемое учитывает влияние тока, циркулирующего в экране.	$$ Z_0 = (Z_{\text{ж}} + 2Z_{\text{к}}) — \frac{(Z_{\text{жэ}} + 2Z_{\text{к}})^2}{Z_{\text{э}} + 2Z_{\text{к}}} $$ Экраны работают как параллельный проводник, резко снижая \(Z_0\).
Транспозиция экранов (Cross-Bonding)	\( Z_1 \approx Z_{\text{ж}} — Z_{\text{к}} \) При идеальной транспозиции токи прямой последовательности в экранах подавлены.	$$ Z_0 = (Z_{\text{ж}} + 2Z_{\text{к}}) — \frac{(Z_{\text{жэ}} + 2Z_{\text{к}})^2}{Z_{\text{э}} + 2Z_{\text{к}}} $$ Для токов нулевой последовательности транспозиция «прозрачна», экраны работают как при двустороннем заземлении.

Состояние экрана

Сопротивление прямой последовательности ($Z_1$)

Сопротивление нулевой последовательности ($Z_0$)

Одностороннее заземление
(или транспозиция, см. прим.)

$ Z_1 = Z_{\text{ж}} — Z_{\text{к}} $

Примечание: Здесь экран не влияет на $Z_1$, так как ток в нем равен нулю.

$ Z_0 = Z_{\text{ж}} + 2Z_{\text{к}} $

Примечание: Ток возвращается только через землю.

Двустороннее заземление
(Solid Bonding)

$$ Z_1 = (Z_{\text{ж}} — Z_{\text{к}}) + \frac{(Z_{\text{к}} — Z_{\text{жэ}})^2}{Z_{\text{э}} — Z_{\text{к}}} $$

Второе слагаемое учитывает влияние тока, циркулирующего в экране.

$$ Z_0 = (Z_{\text{ж}} + 2Z_{\text{к}}) — \frac{(Z_{\text{жэ}} + 2Z_{\text{к}})^2}{Z_{\text{э}} + 2Z_{\text{к}}} $$

Экраны работают как параллельный проводник, резко снижая $Z_0$.

Транспозиция экранов
(Cross-Bonding)

$ Z_1 \approx Z_{\text{ж}} — Z_{\text{к}} $

При идеальной транспозиции токи прямой последовательности в экранах подавлены.

$$ Z_0 = (Z_{\text{ж}} + 2Z_{\text{к}}) — \frac{(Z_{\text{жэ}} + 2Z_{\text{к}})^2}{Z_{\text{э}} + 2Z_{\text{к}}} $$

Для токов нулевой последовательности транспозиция «прозрачна», экраны работают как при двустороннем заземлении.

Важно: Обратите внимание, что для нулевой последовательности ($Z_0$) режим транспозиции экранов эквивалентен режиму двустороннего заземления. Это значит, что при расчете токов однофазного КЗ транспонированная линия ведет себя как линия с глухозаземленными экранами — экраны забирают на себя значительную часть тока КЗ, разгружая землю.

5. Практические примеры и анализ результатов

Для демонстрации физики процессов рассмотрим результаты численного моделирования для двух распространенных классов напряжения.

Пример №1. Кабельная линия 10 кВ (Среднее напряжение)

Жила: Медь, 240 мм²
Экран: Медь, 50 мм²
Грунт: $\rho = 100 \, \text{Ом}\cdot\text{м}$

Таблица 7. Результаты расчета для кабеля 10 кВ (Ом/км)

Прокладка	Схема экранов	Прямая посл. ($Z_1$)		Нулевая посл. ($Z_0$)
Прокладка	Схема экранов	$R_1$	$X_1$	$R_0$	$X_0$
Треугольник (вплотную)	Одностороннее	0.083	0.091	0.231	2.036
	Двустороннее	0.094	0.089	0.463	0.099
	Транспозиция	0.083	0.091	0.463	0.099
В плоскости (S = 100 мм)	Одностороннее	0.083	0.188	0.231	1.843
	Двустороннее	0.140	0.164	0.459	0.105
	Транспозиция	0.083	0.188	0.459	0.105

Пример №2. Кабельная линия 110 кВ (Высокое напряжение)

Жила: Медь, 1000 мм² (типа «Милликен»)
Экран: Медь, 185 мм²

Таблица 8. Результаты расчета для кабеля 110 кВ (Ом/км)

Прокладка	Схема экранов	Прямая посл. ($Z_1$)		Нулевая посл. ($Z_0$)
Прокладка	Схема экранов	$R_1$	$X_1$	$R_0$	$X_0$
Треугольник	Одностороннее	0.020	0.092	0.168	1.899
	Двустороннее	0.042	0.081	0.127	0.043
	Транспозиция	0.020	0.092	0.127	0.043

Анализ:

Влияние на $R_1$: При двустороннем заземлении (особенно при прокладке в плоскости) активное сопротивление прямой последовательности $R_1$ возрастает значительно (в примере для 10 кВ — с 0.083 до 0.140 Ом/км, почти на 70%!). Это происходит из-за появления токов в экранах, которые нагревают кабель. Именно поэтому для мощных линий применяют транспозицию, которая возвращает $R_1$ к значению, как при одностороннем заземлении.
Коллапс $X_0$: Обратите внимание на реактивное сопротивление нулевой последовательности $X_0$. При заземлении экранов (двустороннем или транспозиции) оно падает в 15-40 раз (с ~1.9 до ~0.043 Ом/км). Это объясняется эффектом экранирования: токи в экране текут в противофазе току в жиле (трансформаторный эффект), компенсируя магнитное поле и снижая индуктивность.

6. Глубокий анализ индуктивности: Внутренние слагаемые и ошибки упрощения

При проектировании кабельных линий инженеры часто сталкиваются с парадоксом: данные заводских каталогов могут расходиться с результатами расчетов в специализированных программных комплексах. Корни этого расхождения кроются в упрощенных методиках, которые исторически сложились для воздушных линий, но некорректно переносятся на кабельные.

6.1. Анатомия заводской формулы

Большинство фирм-изготовителей кабельной продукции в своих технических спецификациях приводят следующую формулу для определения погонной индуктивности (мГн/км):

L_{\text{кат}} = 0.2 \ln \left( \frac{S}{r_1} \right) \quad [\text{мГн/км}] \quad (2)

Где:

$ S $ — расстояние между осями токопроводящих жил;

$ r_1 $ — радиус токопроводящей жилы.

Проблема интерпретации: Производители редко указывают, для какого режима (прямой или нулевой последовательности) и для какой схемы заземления экранов справедлива эта формула. Более того, она является физически неполной.

6.2. Внутренняя индуктивность: Скрытое слагаемое

Формула (2) описывает только внешнюю индуктивность — магнитный поток, сцепленный с контуром, проходящий через пространство между жилами. Однако ток протекает по всему сечению жилы, создавая магнитное поле и внутри самого металла проводника.

Согласно теории электромагнитного поля, внутренняя индуктивность $ L_{\text{вн}} $ цилиндрического проводника (при условии равномерного распределения тока по сечению, то есть на низких частотах) является константой и не зависит от радиуса жилы.

L_{\text{вн}} = \frac{\mu_0}{8\pi} = \frac{4\pi \cdot 10^{-7}}{8\pi} = 0.5 \cdot 10^{-7} \, \text{Гн/м} = 0.05 \, \text{мГн/км}

Таким образом, истинная собственная индуктивность жилы $ L_{\text{ж}} $ и экрана $ L_{\text{э}} $ должна включать это слагаемое. Полные формулы (с учетом внутренней индуктивности) выглядят так:

L_{\text{ж}} = L_{\text{вн}} + \frac{\mu_0}{2\pi} \ln \left( \frac{D_{\text{з}}}{r_1} \right) = 0.05 \cdot 10^{-6} + 0.2 \cdot 10^{-6} \ln \left( \frac{D_{\text{з}}}{r_1} \right) $$ $$ L_{\text{э}} = L_{\text{вн}} + \frac{\mu_0}{2\pi} \ln \left( \frac{D_{\text{з}}}{r_2} \right)

6.3. Почему для кабелей это критично?

Возникает закономерный вопрос: почему в справочниках по воздушным линиям (ВЛ) внутренней индуктивностью часто пренебрегают, а для кабелей это считается ошибкой?

Все дело в соотношении геометрии:

Для ВЛ: Расстояние между фазами $ S $ составляет несколько метров (например, 3–5 м), а радиус провода $ r_1 $ — сантиметры. Отношение $ S/r_1 $ велико, логарифм $ \ln(S/r_1) $ дает большое число. На его фоне добавка $ 0.05 $ составляет менее 1–2% и тонет в погрешностях провиса провода.
Для КЛ: Фазы проложены вплотную (треугольником) или очень близко. Расстояние $ S $ соизмеримо с диаметром кабеля. Логарифм получается небольшим, и «потерянное» слагаемое $ 0.05 $ мГн/км начинает вносить существенный вклад в общий импеданс.

Аналогия с логистикой: Представьте, что вы рассчитываете время доставки груза.

Если вы везете груз из Москвы во Владивосток (Воздушная линия), то время, затраченное на выезд со склада на трассу (внутренняя индуктивность), ничтожно мало по сравнению с неделей пути. Им можно пренебречь.

Но если вы доставляете пиццу в соседний дом (Кабельная линия), то время спуска по лестнице и выхода из подъезда (внутренняя индуктивность) составляет 30-40% от всего времени доставки. Игнорировать его нельзя.

6.4. Аналитическое доказательство и оценка погрешности

Используя формулы из Таблицы 3.7 (часть 1) и подставляя полные выражения индуктивностей, можно показать, что сопротивление прямой последовательности $ Z_1 $ для схемы с односторонним заземлением равно:

Z_1 = Z_{\text{ж}} — Z_{\text{к}} = (R_{\text{ж}} + j\omega L_{\text{ж}}) — j\omega M_{\text{к}} $$ $$ L_1 = L_{\text{ж}} — M_{\text{к}} = \left( L_{\text{вн}} + \frac{\mu_0}{2\pi} \ln \frac{D_{\text{з}}}{r_1} \right) — \left( \frac{\mu_0}{2\pi} \ln \frac{D_{\text{з}}}{S} \right) $$ $$ L_1 = L_{\text{вн}} + \frac{\mu_0}{2\pi} \left( \ln \frac{D_{\text{з}}}{r_1} — \ln \frac{D_{\text{з}}}{S} \right) = \mathbf{0.05 + 0.2 \ln \left( \frac{S}{r_1} \right)} \quad [\text{мГн/км}]

Вывод: Заводская формула (2) верна только при условии $ L_{\text{вн}} \approx 0 $. Но еще опаснее другое заблуждение. Расчеты показывают:

При одностороннем заземлении (или транспозиции) формула (2) дает погрешность, равную лишь неучету $ L_{\text{вн}} $.
При двустороннем заземлении (Solid Bonding) формула (2) дает колоссальную ошибку. Реальная индуктивность из-за влияния токов экрана будет меньше. Использование каталожной формулы (2) для кабелей с двусторонним заземлением завышает индуктивность на 1% … 50%!
- Малая ошибка (единицы процентов) — при прокладке треугольником.
- Огромная ошибка (до 50%) — при прокладке в плоскости с зазором.

7. Физика «Земли»: Параметры обратного провода и мифы о глубине $ D_{\text{з}} $

Одной из самых загадочных величин в уравнениях является $ D_{\text{з}} $ — эквивалентная глубина возврата тока в земле. Понимание ее физического смысла необходимо для корректного расчета режимов нулевой последовательности (ОЗЗ, КЗ на землю).

7.1. Независимость прямой последовательности от земли

В формулах сопротивлений (Таблица 3.4 и 3.7) параметр $ D_{\text{з}} $ входит в состав выражений для $ Z_{\text{ж}}, Z_{\text{э}}, Z_{\text{к}} $. Может показаться, что сопротивление прямой последовательности $ Z_1 $ тоже зависит от свойств грунта.

Однако, если подставить полные выражения в формулу $ Z_1 = Z_{\text{ж}} — Z_{\text{к}} $, мы увидим математическое сокращение:

\ln \left( \frac{D_{\text{з}}}{r_1} \right) — \ln \left( \frac{D_{\text{з}}}{S} \right) = \ln \left( \frac{D_{\text{з}}}{r_1} \cdot \frac{S}{D_{\text{з}}} \right) = \ln \left( \frac{S}{r_1} \right)

Слагаемое $ D_{\text{з}} $ (и, следовательно, удельное сопротивление грунта $ \rho_{\text{з}} $) полностью исчезает из уравнения.

Физический смысл: В симметричном режиме прямой последовательности сумма токов трех фаз равна нулю ($ I_A + I_B + I_C = 0 $). Ток в землю не вытекает. Магнитные поля, проникающие глубоко в землю, взаимно компенсируются. Поэтому для нормального режима работы и трехфазных КЗ свойства грунта не важны.

7.2. Проблема глубины $ D_{\text{з}} $ для городской среды

Параметр $ D_{\text{з}} $ (глубина проникновения тока в землю) рассчитывается по классической формуле:
$$ D_{\text{з}} = 2.24 \sqrt{\frac{\rho_{\text{з}}}{\mu_0 \omega}} $$
Для грунта с $ \rho = 100 \, \text{Ом}\cdot\text{м} $ эта глубина составляет почти 1000 метров!

Эта теория прекрасно работает для линий, проходящих в чистом поле. Однако кабельные линии прокладываются в городах. Городская земля («урбанизированный грунт») — это не однородная почва, а слоеный пирог из:

Металлических трубопроводов (водопровод, отопление, газ).
Железобетонных фундаментов и коллекторов.
Оболочек соседних кабельных линий.
Трамвайных рельсов.

Все эти элементы являются проводниками, расположенными параллельно трассе кабеля. Ток нулевой последовательности «ленив» — он не пойдет на глубину 1 км, если рядом, на глубине 2 метра, лежит огромная стальная труба теплотрассы.

Следствие: Реальная эквивалентная глубина $ D_{\text{з}} $ в городе резко снижается.

7.3. Концевой эффект (End Effect)

Вторая проблема применения классической теории к кабелям — это их длина.
Теория Карсона-Поллачека предполагает, что линия «бесконечно длинная». Это позволяет току постепенно «диффундировать» в землю на расчетную глубину.

Для воздушных линий длиной 100-500 км это условие выполняется — концевыми участками (где ток входит и выходит из земли) можно пренебречь.
Но кабельная линия 6-110 кВ часто имеет длину всего 500 метров – 3 км. Это соизмеримо или даже меньше, чем расчетная глубина $ D_{\text{з}} $.

Аналогия с бассейном: Представьте, что ток — это пловец, который хочет нырнуть до дна (глубина $ D_{\text{з}} $).

В длинном бассейне (ВЛ) он успевает нырнуть, проплыть по дну и всплыть.

В коротком «лягушатнике» (КЛ) он едва успевает погрузиться, как уже упирается в бортик (конец линии). Он физически не успевает достичь расчетной глубины.

7.4. Практические рекомендации

На основании вышеизложенного, при расчете уставок земляной защиты для кабельных линий рекомендуется:

Не полагаться слепо на формулу Карсона с $ \rho_{\text{грунта}} $.
Принимать расчетное значение $ D_{\text{з}} $ существенно меньшим (порядка десятков метров), либо использовать эмпирические данные замеров $ Z_0 $ для аналогичных трасс.
Помнить, что завышение $ D_{\text{з}} $ в расчетах ведет к завышению $ Z_0 $, что может привести к нечувствительности релейной защиты при реальном коротком замыкании.

8. Сводная таблица сравнения методов заземления экранов

Для облегчения выбора технического решения приводим итоговое сравнение.

Характеристика	Одностороннее заземление	Двустороннее заземление (Solid Bonding)	Транспозиция (Cross-Bonding)
Сложность монтажа	Низкая	Самая низкая	Высокая (требуются спец. коробки и коаксиальный кабель)
Потери в экранах	Минимальные (тока нет)	Высокие (значительные циркулирующие токи)	Низкие (векторная компенсация ЭДС)
Пропускная способность линии	Максимальная	Снижена на 10-30% из-за нагрева экранов	Близка к максимальной
Напряжение на экране	Растет линейно с длиной. Требует установки ОПН. Ограничивает длину линии.	Нулевое (безопасно)	Ограничено (обычно до 2-4 кВ в аварийных режимах в узлах транспозиции)
Область применения	Короткие линии (< 1-2 км), 6-110 кВ	Низкое/среднее напряжение, короткие перемычки, подводные кабели	Протяженные линии 110-500 кВ высокой мощности

Заключение

В рамках данного материала из двух частей мы подробно рассмотрели методику расчета параметров современных однофазных силовых кабелей.

Геометрия: Точность расчета начинается с корректного определения радиусов слоев, где важно учитывать реальные коэффициенты заполнения многопроволочных жил, а не просто номинальное сечение.
Физика процесса: Кабельная линия — это не просто три провода. Это сложная система индуктивно связанных контуров «жила-экран» и «экран-земля». Игнорирование взаимоиндукции приводит к грубым ошибкам.
Влияние заземления: Показано, что способ соединения экранов кардинально меняет параметры кабеля. Активное сопротивление прямой последовательности $R_1$ может возрастать на 50-70% при глухом заземлении экранов из-за циркулирующих токов. Реактивное сопротивление нулевой последовательности $X_0$ зависит от схемы заземления еще сильнее — разница достигает порядков.

Представленные формулы и методики позволяют инженерам выполнять расчеты с высокой точностью, обеспечивая надежность электроснабжения и корректную работу устройств релейной защиты.

Список нормативной базы и литературы

ГОСТ Р 55025-2012. Кабели силовые с пластмассовой изоляцией на номинальное напряжение от 6 до 35 кВ включительно. Общие технические условия.
СТО 56947007-29.060.20.071-2011. Силовые кабели. Методические указания по выбору и применению силовых кабелей с изоляцией из сшитого полиэтилена 6-35 кВ (ПАО «ФСК ЕЭС»).
IEC 60287-1-1. Electric cables — Calculation of the current rating — Part 1-1: Current rating equations (100% load factor) and calculation of losses — General.
Дмитриев М.В. Заземление экранов однофазных силовых кабелей 6-500 кВ. — СПб.: Изд-во Политехн. ун-та, 2010.
Dommel H.W. EMTP Theory Book (ElectroMagnetic Transients Program). — BPA, Portland, 1986.

Методика расчета продольных параметров однофазных силовых кабелей