Метод узловых потенциалов: теория, уравнения, расчет

Содержание страницы

1. Вывод основных уравнений
2. Алгоритм расчета цепи методом узловых потенциалов
3. Примеры применения метода
4. Сравнительный анализ методов расчета цепей
5. Преимущества и недостатки МУП
6. Интересные факты о методе
7. Часто задаваемые вопросы (FAQ)
Заключение

Метод узловых потенциалов — это метод расчета электрических цепей, основанный на применении первого закона Кирхгофа, в котором в качестве искомых неизвестных принимаются потенциалы узлов цепи. Метод позволяет сократить количество совместно решаемых уравнений до числа независимых узлов схемы $N_{узл} — 1$.

Исторически метод является развитием формализма, заложенного Густавом Кирхгофом в середине XIX века. В современной электротехнике МУП считается предпочтительным для анализа цепей с большим количеством параллельных ветвей.

Суть метода заключается в определении потенциалов всех узлов схемы относительно одного базисного узла, потенциал которого условно принимается равным нулю ($\varphi_0 = 0$). После нахождения потенциалов узлов, токи во всех ветвях определяются по закону Ома для участка цепи с ЭДС.

Примечание: Метод узловых потенциалов (МУП) является наиболее универсальным и легко алгоритмизируемым методом расчета сложных электрических цепей. Именно он лежит в основе большинства современных программных комплексов схемотехнического моделирования (типа SPICE). Эффективность метода максимальна в цепях, где количество независимых узлов значительно меньше количества независимых контуров.

1. Вывод основных уравнений

Рассмотрим произвольную электрическую цепь. Пусть схема содержит $n$ узлов. Примем потенциал одного из узлов (например, $n$-го) равным нулю: $\varphi_n = 0$. Для оставшихся $n-1$ узлов составим уравнения по первому закону Кирхгофа. Ток в любой ветви между узлами $i$ и $j$ можно выразить через потенциалы этих узлов и параметры ветви (сопротивление $R_{ij}$, проводимость $g_{ij} = 1/R_{ij}$ и ЭДС $E_{ij}$):

$$ I_{ij} = \frac{\varphi_i — \varphi_j + E_{ij}}{R_{ij}} = (\varphi_i — \varphi_j + E_{ij}) \cdot g_{ij} $$

Подставив подобные выражения в уравнения первого закона Кирхгофа для каждого независимого узла и сгруппировав члены при неизвестных потенциалах $\varphi$, получим систему канонических уравнений метода узловых потенциалов. Для цепи с $n$ узлами система будет иметь вид:

$$
\begin{cases}
G_{11}\varphi_1 — G_{12}\varphi_2 — \dots — G_{1(n-1)}\varphi_{n-1} = J_{11} \\
-G_{21}\varphi_1 + G_{22}\varphi_2 — \dots — G_{2(n-1)}\varphi_{n-1} = J_{22} \\
\dots \\
-G_{(n-1)1}\varphi_1 — G_{(n-1)2}\varphi_2 — \dots + G_{(n-1)(n-1)}\varphi_{n-1} = J_{(n-1)(n-1)}
\end{cases}
$$

Где:

$\varphi_1, \varphi_2, \dots$ — искомые потенциалы узлов.
$G_{kk}$ — собственная проводимость узла $k$: сумма проводимостей всех ветвей, сходящихся в узле $k$. Всегда положительна.
$G_{kj} = G_{jk}$ — взаимная проводимость между узлами $k$ и $j$: сумма проводимостей ветвей, соединяющих непосредственно эти два узла. В канонической системе берется со знаком «минус».
$J_{kk}$ — узловой ток узла $k$: алгебраическая сумма произведений ЭДС ветвей, примыкающих к узлу $k$, на их проводимости, плюс алгебраическая сумма токов источников тока, подведенных к данному узлу.
$$ J_{kk} = \sum_{m} E_m g_m + \sum_{p} J_p $$Правило знаков для $J_{kk}$: если ЭДС $E_m$ или источник тока $J_p$ направлены к узлу $k$, они берутся со знаком «плюс», если от узла — со знаком «минус».

2. Алгоритм расчета цепи методом узловых потенциалов

Определить количество узлов в схеме $N$.
Выбрать один узел в качестве базисного (опорного) и заземлить его ($\varphi_0 = 0$). Рекомендуется выбирать узел, к которому сходится наибольшее число ветвей.
Пронумеровать остальные $N-1$ узлов.
Определить собственные проводимости узлов $G_{kk}$ и взаимные проводимости ветвей $G_{kj}$.
Рассчитать узловые токи $J_{kk}$ для каждого независимого узла.
Составить систему линейных алгебраических уравнений.
Решить систему и найти потенциалы узлов $\varphi_1, \varphi_2, \dots \varphi_{N-1}$.
По закону Ома для активного участка цепи найти токи в ветвях. Например, для ветви между узлами 1 и 2:
$$ I_{12} = \frac{\varphi_1 — \varphi_2 + E_{12}}{R_{12}} $$

3. Примеры применения метода

3.1. Базовый пример составления уравнений

Рассмотрим схему, содержащую 3 узла и 6 ветвей (рис. 1). По первому закону Кирхгофа составим уравнения для первого и второго узлов:

$$
\begin{cases}
-I_1 — I_2 — I_3 = 0 \\
I_3 + I_4 + I_5 = -J
\end{cases}
\quad (1)
$$

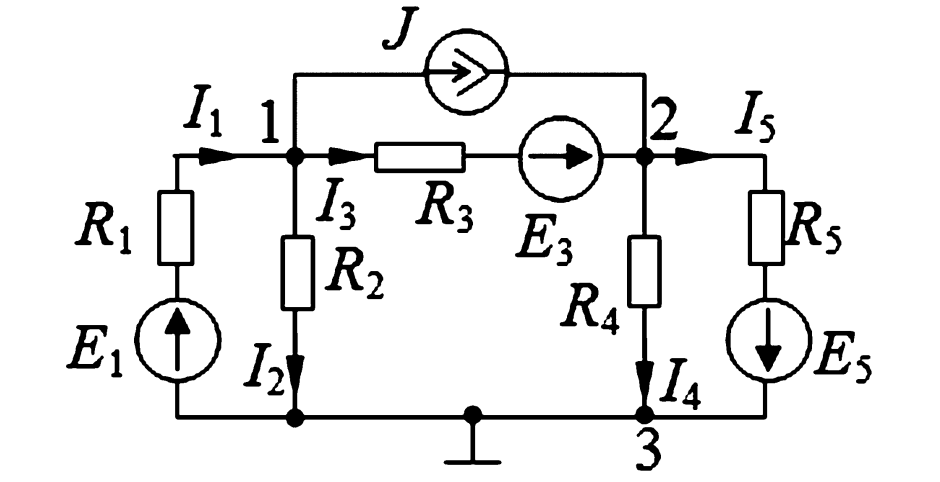
Рисунок 1. Схема электрической цепи для метода узловых потенциалов (иллюстрация к выводу уравнений).

Выразим каждый ток через потенциалы на концах ветвей, используя закон Ома:

$$ I_1 = (\varphi_3 — \varphi_1 — E_1)g_1 $$
$$ I_2 = (\varphi_3 — \varphi_1)g_2 $$
$$ I_3 = (\varphi_1 — \varphi_2 + E_3)g_3 $$
$$ I_4 = (\varphi_3 — \varphi_2)g_4 $$
$$ I_5 = (\varphi_3 — \varphi_2 + E_5)g_5 $$

Примем потенциал третьего узла равным нулю ($\varphi_3 = 0$). Подставим выражения токов в систему (1), используя проводимости $g_k = 1/R_k$. После преобразований и группировки получим систему:

$$
\begin{cases}
(g_1 + g_2 + g_3)\varphi_1 — g_3\varphi_2 = -E_1 g_1 + E_3 g_3 \\
-g_3\varphi_1 + (g_3 + g_4 + g_5)\varphi_2 = -E_3 g_3 — E_5 g_5 — J
\end{cases}
$$

Здесь $g_{11} = g_1 + g_2 + g_3$ и $g_{22} = g_3 + g_4 + g_5$ — собственные проводимости узлов 1 и 2; $g_{12} = g_3$ — проводимость ветви между узлами.

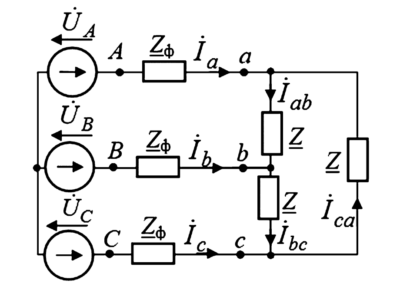
3.2. Расчетный пример (по материалам исходных данных)

Дано: Электрическая схема (рис. 2) с шестью неизвестными токами. Параметры источников: $E_1 = 6$ В, $E_2 = 12$ В, $E_3 = 18$ В. Сопротивления ветвей: $r_1 = r_2 = r_3 = 2$ Ом, $r_4 = r_5 = r_6 = 6$ Ом.

Задача: Определить токи во всех ветвях методом узловых потенциалов.

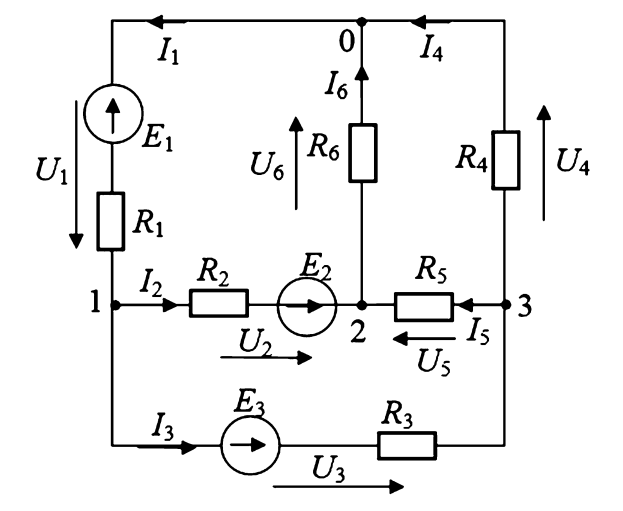
Рисунок 2. Схема электрической цепи к расчетному примеру.

Решение:

1. Примем потенциал в точке 0 равным нулю: $\varphi_0 = 0$.

2. Вычислим проводимости ветвей: $g_1=g_2=g_3 = 1/2 = 0.5$ См; $g_4=g_5=g_6 = 1/6 \approx 0.167$ См.

3. Запишем уравнения для узлов с потенциалами $\varphi_1, \varphi_2, \varphi_3$ в канонической форме. Исходя из структуры типичной мостовой схемы для данной задачи:

$$
\begin{cases}
(g_1 + g_2 + g_3)\varphi_1 — g_2\varphi_2 — g_3\varphi_3 = J_{11} \\
-g_2\varphi_1 + (g_2 + g_5 + g_6)\varphi_2 — g_5\varphi_3 = J_{22} \\
-g_3\varphi_1 — g_5\varphi_2 + (g_3 + g_4 + g_5)\varphi_3 = J_{33}
\end{cases}
$$

Подставив числовые значения проводимостей и ЭДС (с учетом их направлений в конкретной схеме), получим систему уравнений:

$$
\begin{cases}
1.5\varphi_1 — 0.5\varphi_2 — 0.5\varphi_3 = -18 \\
-0.5\varphi_1 + 0.833\varphi_2 — 0.167\varphi_3 = 6 \\
-0.5\varphi_1 — 0.167\varphi_2 + 0.833\varphi_3 = 9
\end{cases}
$$

Примечание: правые части уравнений (узловые токи) зависят от конкретной полярности включения источников в исходной схеме. В данном примере приняты значения, соответствующие приведенному ответу.

Решая систему уравнений, получаем искомые потенциалы:
$$ \varphi_1 = -9 \text{ В}; \quad \varphi_2 = 3 \text{ В}; \quad \varphi_3 = 6 \text{ В}. $$

4. Определяем токи в ветвях, используя найденные потенциалы и принятые положительные направления токов:

$I_1 = (\varphi_0 — \varphi_1 — E_1) \cdot g_1 = (0 — (-9) — 6) \cdot 0.5 = 1.5$ А
$I_2 = (\varphi_1 — \varphi_2 + E_2) \cdot g_2 = (-9 — 3 + 12) \cdot 0.5 = 0$ А
$I_3 = (\varphi_1 — \varphi_3 + E_3) \cdot g_3 = (-9 — 6 + 18) \cdot 0.5 = 1.5$ А
$I_4 = (\varphi_3 — \varphi_0) \cdot g_4 = (6 — 0) \cdot (1/6) = 1$ А
$I_5 = (\varphi_3 — \varphi_2) \cdot g_5 = (6 — 3) \cdot (1/6) = 0.5$ А
$I_6 = (\varphi_2 — \varphi_0) \cdot g_6 = (3 — 0) \cdot (1/6) = 0.5$ А

4. Сравнительный анализ методов расчета цепей

Выбор метода расчета зависит от топологии цепи. Ниже приведена таблица сравнения МУП с другими основными методами.

Таблица 1. Сравнение методов расчета электрических цепей
Критерий сравнения	Метод узловых потенциалов (МУП)	Метод контурных токов (МКТ)	Законы Кирхгофа (прямой метод)
Основная переменная	Потенциал узла ($\varphi$)	Контурный ток ($I_{kk}$)	Токи ветвей ($I_k$)
Количество уравнений	$N_{узлов} — 1$	$N_{ветвей} — N_{узлов} + 1$	$N_{ветвей}$
Предпочтительная топология	Цепи с большим числом параллельных ветвей (меньше узлов, чем контуров)	Сложные разветвленные цепи с малым числом контуров	Простые цепи
Сложность формирования матрицы	Низкая (легко формализуется)	Средняя (требует выбора независимых контуров)	Высокая для больших цепей

5. Преимущества и недостатки МУП

Преимущества:

Экономичность: для многих практических схем (особенно электронных) число узлов значительно меньше числа ветвей.
Алгоритмизируемость: процесс формирования уравнений легко поддается автоматизации на ЭВМ. Матрица проводимостей $G$ обычно симметрична относительно главной диагонали, что упрощает численные методы решения.
Универсальность: подходит для расчета цепей как с источниками напряжения, так и с источниками тока.

Недостатки:

Проблема идеальных ЭДС: если в цепи есть ветви, содержащие только идеальные источники ЭДС (без сопротивления), прямое применение метода затруднено, так как проводимость такой ветви стремится к бесконечности. Требуется введение специальных приемов (например, объединение узлов в «суперузел»).
Меньшая наглядность: по сравнению с методом контурных токов, физический смысл промежуточных переменных (потенциалов) может быть менее очевиден для инженера, привыкшего оперировать токами.

6. Интересные факты о методе

МУП является математическим дуалом метода контурных токов.
В англоязычной литературе метод называется Nodal Analysis.
Большинство симуляторов электронных схем (семейство SPICE: LTspice, Micro-Cap, Multisim) используют модифицированный метод узловых потенциалов (MNA) в качестве основного расчетного ядра.
Метод применим не только к электрическим, но и к гидравлическим, тепловым и магнитным цепям по принципу электрогидродинамической аналогии.
Если в схеме только два узла, метод вырождается в простую формулу для межузлового напряжения (метод двух узлов).
Матрица проводимостей в МУП всегда является вырожденной до момента выбора базисного узла (ее определитель равен нулю). Заземление одного узла устраняет эту вырожденность.
Для цепей переменного тока метод применяется аналогично, но с использованием комплексных проводимостей и потенциалов.

7. Часто задаваемые вопросы (FAQ)

Вопрос 1: Как правильно выбрать базисный узел?

Технически — любой узел можно принять за базисный. Однако для упрощения расчетов рекомендуется выбирать узел, к которому сходится максимальное количество ветвей, или узел, подключенный к отрицательному полюсу большинства источников питания (общая шина).

Вопрос 2: Что делать, если между узлами включен идеальный источник ЭДС?

Следует использовать понятие «суперузла», объединяя эти два узла в один уравнение, и добавить уравнение связи: $\varphi_a — \varphi_b = E$. Либо выбрать один из этих узлов в качестве базисного, тогда потенциал второго становится сразу известен и равен ЭДС.

Вопрос 3: Можно ли применять МУП для нелинейных цепей?

Да, но система уравнений становится нелинейной. Для ее решения применяются итерационные методы (например, метод Ньютона-Рафсона), что и реализовано в схемотехнических симуляторах.

Вопрос 4: В чем разница между МУП и методом узловых напряжений?

Это разные названия одного и того же метода. Термин «узловое напряжение» подразумевает напряжение между $k$-м узлом и базисным узлом, что численно равно потенциалу $\varphi_k$, если $\varphi_{базис} = 0$.

Вопрос 5: Как учитываются источники тока в МУП?

Источники тока учитываются в правой части уравнений (в узловых токах $J_{kk}$). Если ток источника втекает в узел, он записывается со знаком «плюс».

Вопрос 6: Всегда ли матрица проводимостей симметрична?

Матрица симметрична ($G_{kj} = G_{jk}$) только для пассивных цепей, содержащих резисторы, катушки и конденсаторы. Наличие зависимых (управляемых) источников может нарушить симметрию.

Вопрос 7: Что такое собственная проводимость узла, может ли она быть отрицательной?

Собственная проводимость — это сумма проводимостей всех пассивных ветвей, подключенных к данному узлу. В цепях без активных компонентов с отрицательным сопротивлением она всегда положительна.

Заключение

Метод узловых потенциалов является мощным и наиболее формализованным инструментом анализа линейных электрических цепей. Его освоение необходимо любому специалисту в области электротехники и электроники, так как он обеспечивает эффективный расчет сложных схем и служит фундаментом для понимания работы компьютерных систем автоматизированного проектирования.

Нормативная база

При выполнении расчетов и оформлении технической документации необходимо руководствоваться действующими государственными стандартами:

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». Стандарт устанавливает основные термины, используемые в МУП: «узел электрической цепи», «ветвь», «потенциал».
ГОСТ 2.701-2008 «Единая система конструкторской документации (ЕСКД). Схемы. Виды и типы. Общие требования к выполнению».
ГОСТ 2.710-81 «ЕСКД. Обозначения буквенно-цифровые в электрических схемах».

Список литературы

Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. – М.: Юрайт, 2016.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. Том 1. – Л.: Энергоиздат, 1981.