Метод симметричных составляющих: теория и применение

Содержание страницы

Основные определения и математический аппарат
Применение метода к анализу цепей
Сравнение симметричных составляющих
Преимущества и ограничения метода
Интересные факты о МСС
Часто задаваемые вопросы (FAQ)
Заключение

Метод симметричных составляющих (МСС) — это фундаментальный математический аппарат, используемый в электротехнике и электроэнергетике для анализа несимметричных (асимметричных) трехфазных электрических цепей. Суть метода заключается в разложении любой несимметричной трехфазной системы векторов (например, токов или напряжений) на три независимые симметричные системы, называемые составляющими.

Этот подход позволяет заменить сложную задачу расчета одной несимметричной цепи на три более простые задачи расчета для каждой из симметричных составляющих, которые затем суммируются для получения итогового решения.

Метод был разработан и предложен в 1918 году канадским инженером-электриком Чарльзом Легейтом Фортескью (Charles Legeyt Fortescue). Его работа «Method of Symmetrical Co-ordinates Applied to the Solution of Polyphase Networks» стала основой для анализа аварийных режимов (коротких замыканий, обрывов фаз) в энергосистемах.

Основные определения и математический аппарат

Любая несимметричная трехфазная система (обозначим ее фазными векторами $ \dot{A} $, $ \dot{B} $, $ \dot{C} $) может быть представлена как сумма трех симметричных систем:

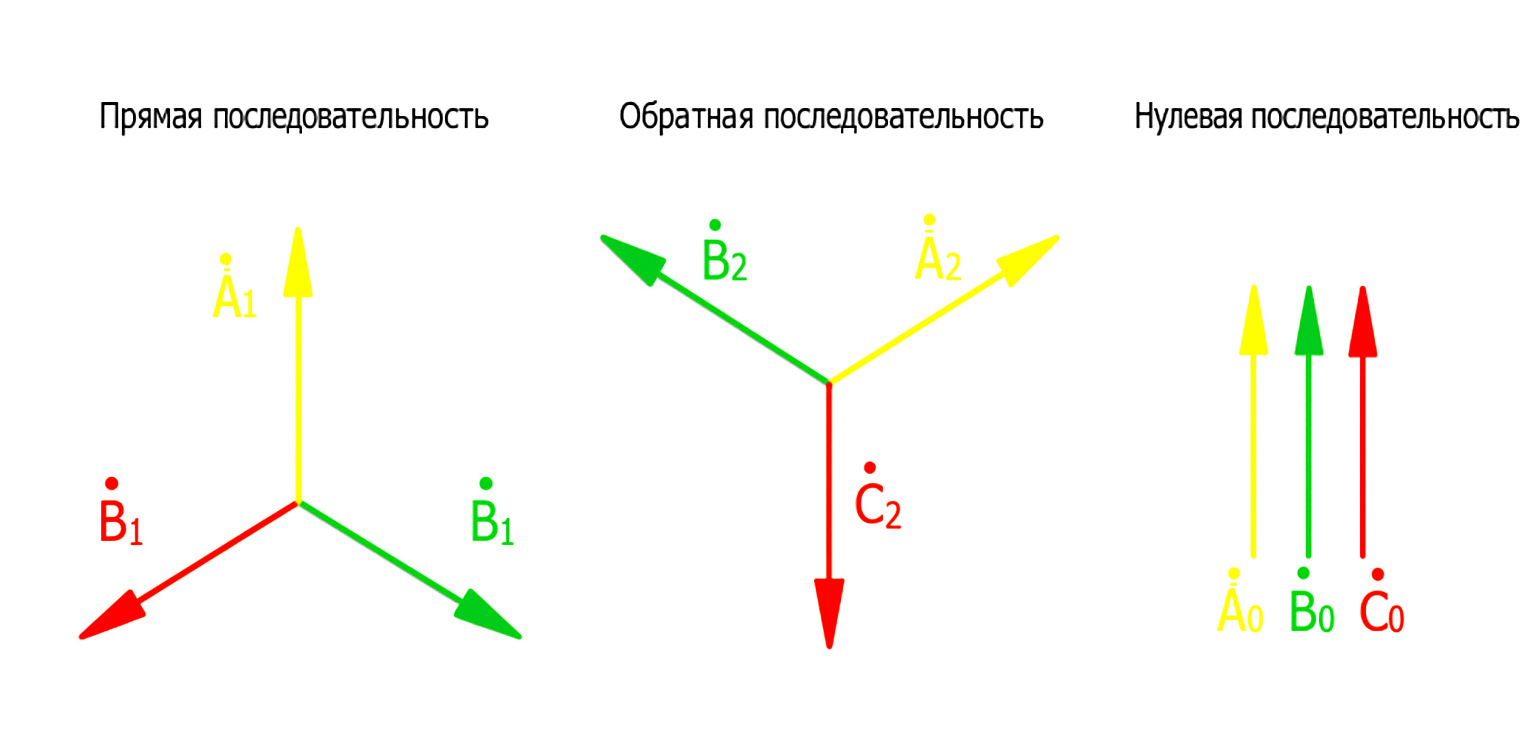
Система прямой последовательности (индекс «1»): Состоит из трех векторов одинаковой величины, сдвинутых друг относительно друга на 120°. Их порядок чередования (A-B-C) совпадает с порядком чередования фаз исходной системы.
Система обратной последовательности (индекс «2»): Состоит из трех векторов одинаковой величины, сдвинутых на 120°, но имеющих обратный порядок чередования (A-C-B).
Система нулевой последовательности (индекс «0»): Состоит из трех векторов, которые равны по величине и совпадают по фазе (сдвиг 0°).

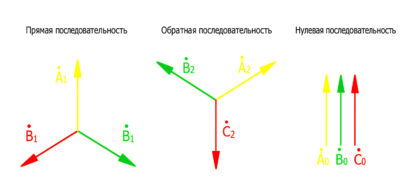
Рисунок 1 — Векторные диаграммы, иллюстрирующие системы:
а) прямой последовательности; б) обратной последовательности; в) нулевой последовательности.

Фазовый оператор $\large{a}$

Для математического описания сдвига фаз вводится комплексный оператор $\large{a}$. Это вектор единичной длины, повернутый на 120° против часовой стрелки:

$$ a = e^{j120^{\circ}} = 1 \angle 120^{\circ} = \cos(120^{\circ}) + j \sin(120^{\circ}) = -0.5 + j0.866 $$

Основные свойства оператора:

$ a^2 = e^{j240^{\circ}} = 1 \angle 240^{\circ} = -0.5 — j0.866 $
$ a^3 = e^{j360^{\circ}} = 1 \angle 360^{\circ} = 1 $
$ a^4 = a $
Важное тождество: $ 1 + a + a^2 = 0 $

Формулы разложения (Анализ)

Зная несимметричные фазные величины (например, напряжения $ \dot{U}_A $, $ \dot{U}_B $, $ \dot{U}_C $), можно найти их симметричные составляющие по следующим формулам:

Составляющая нулевой последовательности:

$$ \dot{U}_0 = \frac{1}{3} (\dot{U}_A + \dot{U}_B + \dot{U}_C) $$

Составляющая прямой последовательности:

$$ \dot{U}_1 = \frac{1}{3} (\dot{U}_A + a\dot{U}_B + a^2\dot{U}_C) $$

Составляющая обратной последовательности:

$$ \dot{U}_2 = \frac{1}{3} (\dot{U}_A + a^2\dot{U}_B + a\dot{U}_C) $$

Аналогичные формулы применяются и для токов $ \dot{I}_A $, $ \dot{I}_B $, $ \dot{I}_C $.

Формулы синтеза

Обратная задача (восстановление фазных величин из симметричных составляющих) решается системой уравнений:

$$ \dot{U}_A = \dot{U}_0 + \dot{U}_1 + \dot{U}_2 $$
$$ \dot{U}_B = \dot{U}_0 + a^2\dot{U}_1 + a\dot{U}_2 $$
$$ \dot{U}_C = \dot{U}_0 + a\dot{U}_1 + a^2\dot{U}_2 $$

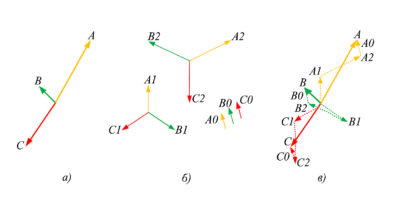
Рисунок 2 — Векторная диаграмма синтеза: а) — показана исходная несимметричная система векторов $ \dot{U}_A, \dot{U}_B, \dot{U}_C $; б) — изображены три симметричные составляющие: прямая (A1, B1, C1), обратная (A2, B2, C2), нулевая (A0, B0, C0); в) — показано, как их сложение даёт исходную несимметричную систему (векторы A, B, C).

Применение метода к анализу цепей

Главное преимущество МСС заключается в том, что в симметричной цепи (где все три фазы имеют одинаковые параметры) токи и напряжения разных последовательностей не влияют друг на друга. Цепь «распадается» на три независимые схемы замещения, каждая для своей последовательности.

Схемы замещения и полные сопротивления

Для каждого элемента энергосистемы (генератор, трансформатор, линия, двигатель) вводятся три различных полных сопротивления:

$ Z_1 $ (Сопротивление прямой последовательности): Это обычное фазное сопротивление элемента в симметричном режиме работы.
$ Z_2 $ (Сопротивление обратной последовательности): Сопротивление, которое элемент оказывает токам обратной последовательности. Для статических элементов (линии, трансформаторы) $ Z_2 \approx Z_1 $. Однако для вращающихся машин (генераторы, двигатели) $ Z_2 $ значительно отличается от $ Z_1 $ из-за того, что поле обратной последовательности вращается против ротора.
$ Z_0 $ (Сопротивление нулевой последовательности): Сопротивление, которое элемент оказывает токам нулевой последовательности. Эти токи одинаковы во всех трех фазах, поэтому они могут протекать, только если есть путь для их замыкания (например, через нейтраль и землю). Для элементов, не имеющих связи с землей (например, соединение «треугольник»), $ Z_0 = \infty $.

Примечание: Понятия прямой и обратной последовательности, лежащие в основе метода, активно используются в современной стандартизации.

Например, ГОСТ 32144-2013 («Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения») напрямую нормирует показатели, основанные на МСС:

Коэффициент несимметрии напряжений по обратной последовательности $ k_{2U} $: Отношение напряжения обратной последовательности $ U_2 $ к напряжению прямой последовательности $ U_1 $. Нормальное значение в точке передачи электроэнергии не должно превышать 2% (длительно).
Коэффициент несимметрии напряжений по нулевой последовательности $ k_{0U} $: Отношение напряжения нулевой последовательности $ U_0 $ к $ U_1 $.

Эти коэффициенты характеризуют степень несимметрии, которая негативно влияет на асинхронные двигатели (вызывая перегрев) и другое оборудование.

Анализ типовых задач

С помощью МСС решаются два основных класса задач.

1. Несимметричный источник, симметричная цепь

Если генератор создает несимметричную систему напряжений ($ \dot{E}_A, \dot{E}_B, \dot{E}_C $), а нагрузка симметрична (сопротивления $ Z_1, Z_2, Z_0 $), расчет ведется по принципу суперпозиции (наложения):

Находятся симметричные составляющие ЭДС: $ \dot{E}_0, \dot{E}_1, \dot{E}_2 $.
Для каждой последовательности независимо находится ее ток:
$$ \dot{I}_0 = \frac{\dot{E}_0}{Z_0} \quad ; \quad \dot{I}_1 = \frac{\dot{E}_1}{Z_1} \quad ; \quad \dot{I}_2 = \frac{\dot{E}_2}{Z_2} $$
Находятся полные фазные токи путем синтеза:
$$ \dot{I}_A = \dot{I}_0 + \dot{I}_1 + \dot{I}_2 $$
$$ \dot{I}_B = \dot{I}_0 + a^2\dot{I}_1 + a\dot{I}_2 $$
$$ \dot{I}_C = \dot{I}_0 + a\dot{I}_1 + a^2\dot{I}_2 $$

2. Симметричный источник, несимметричная цепь (аварийный режим)

Это наиболее частый случай: генератор симметричен ($ \dot{E}_1 \neq 0 $, а $ \dot{E}_0 = 0, \dot{E}_2 = 0 $), но в сети происходит несимметрия (например, короткое замыкание на землю или обрыв фазы).

В этом случае в зоне аварии возникает несимметричная система токов и напряжений. Три схемы замещения (прямая, обратная, нулевая) перестают быть независимыми. Они особым образом соединяются между собой в точке несимметрии.

Например, при однофазном коротком замыкании фазы ‘A’ на землю в точке КЗ выполняются условия: $ \dot{I}_B = 0 $, $ \dot{I}_C = 0 $, $ \dot{U}_A = 0 $. Анализ этих «граничных условий» с помощью формул синтеза показывает, что в этом случае $ \dot{I}_0 = \dot{I}_1 = \dot{I}_2 $. Это означает, что для расчета такого режима все три схемы замещения (прямую, обратную и нулевую) необходимо соединить последовательно.

Сравнение симметричных составляющих

Для лучшего понимания физического смысла, сведем характеристики трех последовательностей в таблицу.

**Таблица 1** — Сравнительная характеристика симметричных составляющих
Параметр	Прямая последовательность (1)	Обратная последовательность (2)	Нулевая последовательность (0)
Порядок фаз	A-B-C (совпадает с системным)	A-C-B (противоположен системному)	Нет чередования (все фазы совпадают)
Магнитное поле в машинах	Вращается синхронно с ротором (основное рабочее поле)	Вращается против ротора с двойной скользящей скоростью	Пульсирующее, не создающее вращающего момента
Влияние на оборудование	Создает полезный крутящий момент (в двигателях)	Создает тормозной момент, вызывает сильный перегрев ротора	Вызывает перегрев в обмотках, создает помехи в линиях связи
Путь протекания тока	По трем фазным проводам (сумма в нейтрали равна нулю)	По трем фазным проводам (сумма в нейтрали равна нулю)	По трем фазным проводам в одном направлении, замыкается через нейтраль и землю
Условие существования	Существует в любом рабочем режиме	Возникает только при несимметрии фазных нагрузок или КЗ	Возникает при несимметрии и только при наличии пути «нейтраль-земля»

Преимущества и ограничения метода

Преимущества

Универсальность: Метод позволяет анализировать любой тип несимметрии (обрывы, короткие замыкания, несимметричные нагрузки).
Упрощение: Сводит одну сложную трехфазную несимметричную задачу к трем более простым, но взаимосвязанным однофазным задачам.
Физическая наглядность: Каждая составляющая имеет четкий физический смысл (рабочее поле, тормозное поле, поле рассеяния), что позволяет оценивать влияние несимметрии на оборудование.
Основа для релейной защиты: Практически все современные цифровые устройства релейной защиты и автоматики (РЗА) непрерывно вычисляют симметричные составляющие для обнаружения аварийных режимов.

Недостатки и ограничения

Линейность: Метод в его классическом виде строго применим только для линейных электрических цепей. При анализе элементов с нелинейными ВАХ (например, трансформаторы в режиме насыщения) требуются специальные допущения.
Сложность определения параметров: Для точного расчета необходимо знать сопротивления $ Z_1, Z_2, Z_0 $ для всех элементов системы, что может быть нетривиальной задачей (особенно для $ Z_0 $).
Трудоемкость (докомпьютерная): Ручной расчет несимметричных режимов, особенно в сложных сетях, очень громоздок, хотя и структурирован.

Интересные факты о МСС

Автор работал на Westinghouse: Ч.Л. Фортескью был ведущим инженером-исследователем в компании Westinghouse, где и разработал свой метод для решения проблем с первыми крупными энергосистемами.
Обратная последовательность «тормозит»: Магнитное поле обратной последовательности в асинхронном двигателе вращается в сторону, противоположную вращению ротора, создавая тормозной момент и вызывая нагрев токами двойной частоты.
«Треугольник» — фильтр для $ I_0 $: Токи нулевой последовательности не могут «выйти» из обмотки, соединенной треугольником (Delta), поскольку у них нет пути к нейтрали. Они циркулируют внутри этого треугольника, что часто используется в трансформаторах.
Основа всех защит: Любое реле, защищающее линию от замыкания на землю, по сути, является измерителем тока или напряжения нулевой последовательности.
Несимметрия снижает КПД: Даже небольшая несимметрия напряжения (наличие $ U_2 $) резко увеличивает потери в асинхронных двигателях.
Метод можно обобщить: МСС является частным случаем более общих математических преобразований (например, преобразование Кларка), используемых для анализа многофазных систем.
Земля как проводник: Сопротивление нулевой последовательности $ Z_0 $ линии электропередачи сильно зависит от типа грунта и наличия грозозащитного троса, так как земля используется как обратный провод для токов $ I_0 $.

Часто задаваемые вопросы (FAQ)

1. Зачем нужен этот метод, если есть мощные компьютеры и ПО?

Современное программное обеспечение (EMTP, PSS/E и др.) не отменяет метод, а использует его в качестве фундаментального алгоритма. Для быстрой оценки режима, настройки релейной защиты и понимания физики процесса МСС незаменим.

2. Что физически означает «оператор $ a $»?

Это математический инструмент, который «поворачивает» вектор на 120° в комплексной плоскости, не изменяя его длины. Это просто удобная форма записи для работы с трехфазными системами, где такой сдвиг является нормой.

3. Почему $ Z_1, Z_2, Z_0 $ разные?

Это связано с физикой. Для вращающихся машин $ Z_1 \neq Z_2 $, так как магнитное поле $ I_1 $ вращается синхронно с ротором, а поле $ I_2 $ — против него, встречая разное сопротивление. $ Z_0 $ отличается, так как путь для токов $ I_0 $ (через нейтраль и землю) конструктивно и геометрически совершенно иной, чем путь для фазных токов.

4. Откуда вообще берется ток нулевой последовательности?

$ I_0 $ появляется только при «металлической» или «электрической» несимметрии относительно земли. Самый частый пример — замыкание одной или двух фаз на землю. В симметричном режиме или при трехфазном КЗ $ I_0 = 0 $.

5. Что такое несимметричная нагрузка?

Это любая нагрузка, которая потребляет разный ток по трем фазам. Классические примеры: однофазные сварочные аппараты, дуговые сталеплавильные печи, или просто большое количество однофазных бытовых потребителей, неравномерно распределенных по фазам в жилом доме.

6. Как МСС связан с ГОСТ 32144-2013?

ГОСТ использует МСС как инструмент измерения качества. Он устанавливает предел на $ k_{2U} = U_2 / U_1 $, то есть на «уровень» нежелательной обратной последовательности. Энергоснабжающая организация обязана следить, чтобы эта величина не превышала 2%.

7. Что опаснее для оборудования: обратная или нулевая последовательность?

Это зависит от оборудования. Для двигателей и генераторов крайне опасна обратная последовательность, вызывающая быстрый перегрев ротора. Для трансформаторов и линий связи опасна нулевая последовательность, которая может вызывать ложные срабатывания защит (влияя на дифференциальные реле) и создавать электромагнитные помехи.

Заключение

Метод симметричных составляющих, предложенный более века назад, остается мощным и незаменимым инструментом в арсенале инженера-электрика. Он превращает хаотичную, на первый взгляд, картину несимметричного режима в упорядоченную систему из трех независимых составляющих.

Понимание основ МСС является ключом к анализу аварийных режимов, правильной настройке релейной защиты и обеспечению качества электроэнергии в современных сложных и разветвленных электроэнергетических системах.

Нормативные документы

ГОСТ 32144-2013 — Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения.
ОСТ Р 54130-2010 — Качество электрической энергии. Термины и определения. (Хотя частично заменен, содержит фундаментальные определения).

Метод симметричных составляющих для анализа несимметричных режимов