Метод контурных токов: принципы, уравнения, примеры

Содержание страницы

1. Теоретические основы метода контурных токов
2. Обобщенная матричная форма МКТ
3. Учет источников тока в методе контурных токов
4. Сравнительный анализ методов расчета
5. Преимущества и недостатки МКТ
6. Интересные факты о методе
7. Часто задаваемые вопросы (FAQ)
Заключение

При анализе разветвленных электрических цепей, содержащих множество узлов и ветвей, прямое использование первого и второго законов Кирхгофа приводит к громоздким системам алгебраических уравнений. Для цепи, имеющей $b$ ветвей и $n$ узлов, необходимо составить $b$ уравнений для нахождения всех токов. С ростом сложности схемы ручной расчет становится крайне трудоемким, а вероятность арифметической ошибки возрастает.

Для оптимизации этого процесса были разработаны методы, позволяющие сократить число необходимых уравнений. Одним из наиболее эффективных является метод контурных токов, который автоматически удовлетворяет первому закону Кирхгофа, требуя составления уравнений только по второму закону для независимых контуров.

Примечание эксперта: Метод контурных токов (МКТ) является одним из фундаментальных методов анализа сложных электрических цепей. Его эффективность основана на снижении размерности системы уравнений по сравнению с прямым применением законов Кирхгофа. Метод формализован Дж. К. Максвеллом и остается базовым инструментом в современной электротехнике и схемотехническом моделировании.

1. Теоретические основы метода контурных токов

В основе метода лежит концепция контурного тока — расчетной величины, которая условно протекает по замкнутому независимому контуру, оставаясь неизменной вдоль всех ветвей этого контура. Реальный ток в любой ветви схемы представляет собой алгебраическую сумму контурных токов, протекающих через данную ветвь.

Число необходимых уравнений в МКТ равно числу независимых контуров схемы, которое определяется топологией цепи по формуле:

$$N_{yp} = b — n + 1$$

где $b$ — количество ветвей, $n$ — количество узлов.

1.1. Базовые уравнения метода

Рассмотрим принцип формирования уравнений на примере двухконтурной схемы. Пусть в схеме выделены два независимых контура с контурными токами $I_{11}$ и $I_{22}$. Действительный ток в смежной ветви $I_2$ можно выразить через разность этих контурных токов (при условии встречного направления их протекания через общую ветвь):

$$I_2 = I_{11} — I_{22} \quad (1)$$

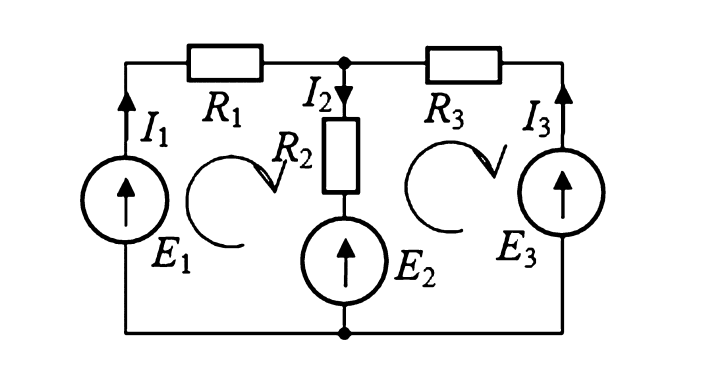
Рисунок 1. Схема электрической цепи с указанием действительных и контурных токов

Составив уравнения по второму закону Кирхгофа для первого и второго контуров и выразив реальные токи через контурные, мы получаем систему:

Для первого контура:

$$I_{11}R_1 + (I_{11} — I_{22})R_2 = E_1 — E_2 \quad (2)$$

Для второго контура (с учетом направлений обхода и ЭДС):

$$(I_{11} — I_{22})R_2 — I_{22}R_3 = E_3 — E_2 \quad (3)$$

После перегруппировки слагаемых система приводится к каноническому виду:

$$\begin{cases} I_{11}(R_1 + R_2) — I_{22}R_2 = E_1 — E_2 \\ -I_{11}R_2 + I_{22}(R_2 + R_3) = E_2 — E_3 \end{cases}$$

Или, вводя обобщенные обозначения сопротивлений и ЭДС:

$$\begin{cases} R_{11}I_{11} — R_{12}I_{22} = E_{11} \\ -R_{21}I_{11} + R_{22}I_{22} = E_{22} \end{cases} \quad (4)$$

1.2. Физический смысл коэффициентов

$R_{ii}$ (например, $R_{11}$, $R_{22}$) — Собственное сопротивление контура: Сумма сопротивлений всех ветвей, входящих в $i$-й контур. Всегда положительная величина.
$R_{ij}$ (например, $R_{12}$, $R_{21}$) — Взаимное (общее) сопротивление контуров: Сопротивление ветви, смежной для контуров $i$ и $j$. Берется со знаком «минус», если контурные токи в этой ветви направлены встречно, и со знаком «плюс», если согласно. При стандартном выборе направлений (все по часовой стрелке) они всегда встречны, отсюда типовой знак «минус» в канонических уравнениях.
$E_{ii}$ (например, $E_{11}$, $E_{22}$) — Контурная ЭДС: Алгебраическая сумма всех источников ЭДС, входящих в контур. ЭДС берется со знаком «плюс», если направление ее стрелки совпадает с направлением обхода контура.

2. Обобщенная матричная форма МКТ

Для цепи с произвольным числом независимых контуров $k$ система уравнений имеет вид:

$$\begin{cases} R_{11}I_{11} + R_{12}I_{22} + \dots + R_{1k}I_{kk} = E_{11} \\ R_{21}I_{11} + R_{22}I_{22} + \dots + R_{2k}I_{kk} = E_{22} \\ \dots \\ R_{k1}I_{11} + R_{k2}I_{22} + \dots + R_{kk}I_{kk} = E_{kk} \end{cases} \quad (5)$$

В компактной матричной форме это записывается как:

$$[R] \cdot [I_k] = [E_k] \quad (6)$$

где $[R]$ — квадратная матрица контурных сопротивлений, $[I_k]$ — вектор-столбец искомых контурных токов, $[E_k]$ — вектор-столбец контурных ЭДС. Для пассивных линейных цепей без управляемых источников матрица $[R]$ симметрична относительно главной диагонали ($R_{ij} = R_{ji}$).

3. Учет источников тока в методе контурных токов

Наличие в схеме идеальных источников тока требует особой методики, так как внутреннее сопротивление такого источника бесконечно велико, и прямое включение его в контурное уравнение невозможно. Источники тока рассматриваются как ветви с уже известными контурными токами.

Оптимальный подход заключается в выборе системы контуров таким образом, чтобы каждый источник тока входил только в один контур. В этом случае контурный ток данного контура становится равным току источника (с учетом знака), и уравнение для этого контура исключается из системы, уменьшая ее размерность.

Рисунок 2 — Анализ цепи при наличии источника тока J

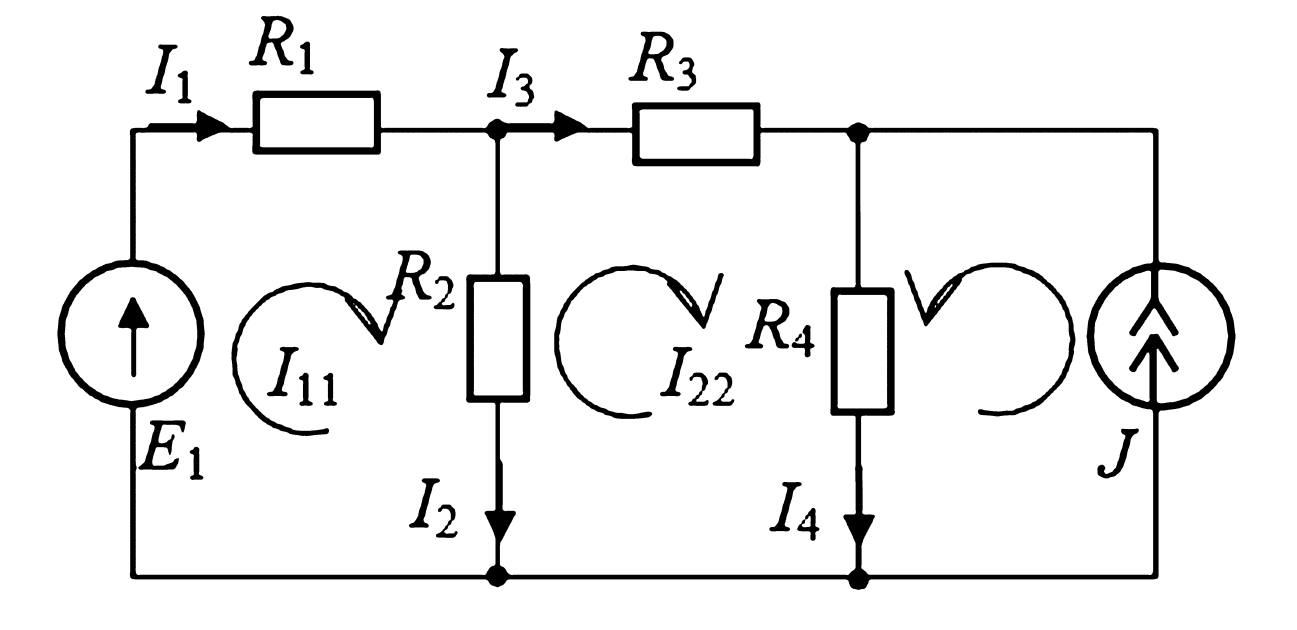
Рассмотрим схему на Рисунке 2. Образуя контур с источником тока $J$, который замыкается через ветвь с сопротивлением $R_4$, мы принимаем соответствующий контурный ток равным $J$. Оставшиеся неизвестные контурные токи $I_{11}$ и $I_{22}$ определяются из системы уравнений:

$$\begin{cases} (R_1 + R_2)I_{11} — R_2 I_{22} = E_1 \\ -R_2 I_{11} + (R_2 + R_3 + R_4)I_{22} + R_4 J = 0 \end{cases} \quad (7)$$

Важно отметить появление слагаемого $R_4 J$ во втором уравнении. Это происходит потому, что через сопротивление $R_4$ протекают два контурных тока: искомый $I_{22}$ и известный $J$ (в одном направлении, если так выбраны контуры). В канонической записи известное слагаемое $R_4 J$ переносится в правую часть уравнения:

$$-R_2 I_{11} + (R_2 + R_3 + R_4)I_{22} = -R_4 J$$

После нахождения $I_{11}$ и $I_{22}$ действительные токи ветвей определяются как:

$$I_1 = I_{11}, \quad I_2 = I_{11} — I_{22}, \quad I_3 = I_{22}, \quad I_4 = I_{22} + J$$

4. Сравнительный анализ методов расчета

Выбор между методом контурных токов и методом узловых потенциалов (МУП) зависит от топологии конкретной схемы. Приведем сравнение для оптимального выбора инженерного подхода.

Таблица 1 — Сравнение Метода Контурных Токов (МКТ) и Метода Узловых Потенциалов (МУП)
Характеристика	Метод Контурных Токов (МКТ)	Метод Узловых Потенциалов (МУП)
Базовые переменные	Контурные токи (фиктивные)	Потенциалы узлов
Количество уравнений	$N_{yp} = b — n + 1$ (число независимых контуров)	$N_{yp} = n — 1$ (число независимых узлов)
Предпочтительная топология	Схемы с малым числом контуров и большим числом узлов. Удобен для планарных схем.	Схемы с большим числом параллельных ветвей (мало узлов, много контуров).
Источники тока	Требуют особого внимания (выбор контуров или суперконтуров).	Учитываются естественно и просто (в правой части уравнений).
Источники ЭДС	Учитываются естественно (в правой части уравнений).	Идеальные ЭДС требуют специальных приемов (суперузлы) или преобразования в источники тока.

5. Преимущества и недостатки МКТ

Преимущества

Значительное сокращение числа уравнений по сравнению с прямым применением законов Кирхгофа.
Высокая степень формализации, что удобно для машинного расчета.
Автоматическое выполнение первого закона Кирхгофа.
Удобство работы со схемами, содержащими много последовательно соединенных элементов и источников напряжения.

Недостатки

Необходимость тщательного выбора независимых контуров в сложных непланарных схемах.
Менее интуитивен при наличии большого количества идеальных источников тока.
Оперирует абстрактными (неизмеряемыми напрямую) величинами — контурными токами.

6. Интересные факты о методе

Метод был систематизирован Джеймсом Клерком Максвеллом, поэтому в англоязычной литературе часто называется «методом циркулирующих токов Максвелла».
Существует полная математическая двойственность между МКТ и методом узловых потенциалов. Уравнения одного метода могут быть преобразованы в уравнения другого для дуальной топологической схемы.
Для планарных схем (которые можно нарисовать без пересечения ветвей) выбор контуров тривиален — это «окна» или ячейки схемы.
Матрица сопротивлений $[R]$ в МКТ всегда является положительно определенной для пассивных цепей, что гарантирует единственность решения.
В современных симуляторах (SPICE) чаще используется модифицированный узловой анализ, однако МКТ остается незаменимым для теоретического понимания работы цепей с магнитной связью.
Если выбрать все контурные токи в одном направлении (например, по часовой стрелке), матрица сопротивлений будет иметь положительные диагональные элементы и отрицательные (или нулевые) внедиагональные.
Понятие «независимый контур» тесно связано с теорией графов: независимые контура формируются добавлением одной хорды к дереву графа цепи.

7. Часто задаваемые вопросы (FAQ)

Вопрос 1: Что произойдет, если неправильно выбрать направление контурного тока?

Ничего критичного. Если реальное направление тока противоположно выбранному, в результате расчета вы получите отрицательное значение контурного тока. Физический смысл сохраняется.

Вопрос 2: Можно ли использовать МКТ для цепей с нелинейными элементами?

Классический матричный МКТ применим только для линейных цепей. Для нелинейных цепей уравнения становятся дифференциальными или нелинейными алгебраическими и решаются итерационными методами.

Вопрос 3: Как быть, если ветвь с источником тока принадлежит сразу двум выбранным контурам?

Это усложняет расчет. В таком случае часто используют понятие «суперконтура», исключая общую ветвь с источником тока и составляя одно уравнение для объединенного контура, плюс уравнение связи токов. Проще перевыбрать контуры так, чтобы источник тока принадлежал только одному из них.

Вопрос 4: Обязательно ли выбирать все контурные токи в одном направлении?

Нет, не обязательно, но настоятельно рекомендуется (обычно по часовой стрелке). Это стандартизирует знаки в уравнениях и снижает вероятность ошибок при их составлении.

Вопрос 5: Что такое «вырожденный» контур?

Это контур, который не содержит ни одной ветви, не входящей в другие контуры. Использование таких контуров приводит к линейно зависимым уравнениям, система не будет иметь единственного решения.

Вопрос 6: Как учитывать зависимые источники в МКТ?

Зависимые источники (управляемые напряжением или током) включаются в уравнения как обычные источники, но их величины выражаются через неизвестные контурные токи. Это может нарушить симметрию матрицы сопротивлений.

Вопрос 7: Применим ли метод для расчета цепей переменного тока?

Да, метод полностью применим для цепей синусоидального тока. В этом случае все сопротивления заменяются на комплексные импедансы ($Z$), а токи и ЭДС — на их комплексные амплитуды или действующие значения.

Заключение

Метод контурных токов является мощным и универсальным инструментом анализа линейных электрических цепей. Позволяя формализовать процесс составления уравнений и снизить их количество, он служит основой как для ручных инженерных расчетов, так и для алгоритмов компьютерного моделирования. Глубокое понимание принципов МКТ необходимо любому специалисту в области электротехники и электроники для эффективного решения задач схемотехнического анализа.

Нормативная база

При выполнении расчетов и оформлении технической документации следует руководствоваться действующими стандартами:

ГОСТ Р 52002-2003 — Электротехника. Термины и определения основных понятий. (Устанавливает фундаментальные определения: электрическая цепь, ветвь, узел, контур).
ГОСТ 2.702-2011 — Единая система конструкторской документации (ЕСКД). Правила выполнения электрических схем.
ГОСТ 19880-74 — Электротехника. Основные понятия и определения. (Используется в части, не противоречащей более новым стандартам).

Список литературы

- Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2024. — 701 с. (Классический фундаментальный учебник, подробно рассматривающий методы анализа линейных и нелинейных цепей).
- Демирчян К. С., Нейман Л. Р., Коровкин Н. В. Теоретические основы электротехники: в 3 т. — СПб.: Питер, 2021. (Современное переиздание одного из наиболее авторитетных курсов ТОЭ с глубокой проработкой теории цепей).
- Фрязинов В. В. Основы теории электрических цепей: учебное пособие. — М.: Высшая школа, 2019. — 320 с. (Практико-ориентированное пособие с большим количеством разобранных примеров применения метода контурных токов).