Магнитные цепи: классификация, характеристики и расчетные формулы

Содержание страницы

1. Классификация и элементы магнитных цепей
2. Методика расчета неразветвленной магнитной цепи
3. Прямая и обратная задачи расчета
4. Расчет разветвленной магнитной цепи
5. Практические примеры расчета
Преимущества и недостатки методов расчета
Интересные факты о магнитных цепях
FAQ: Часто задаваемые вопросы
Заключение

Что такое магнитная цепь? В электротехнике под этим термином понимается совокупность устройств и сред, через которые замыкается магнитный поток. Понимание принципов работы магнитных цепей является фундаментом для проектирования электрических машин, трансформаторов, электромагнитов, реле и измерительных приборов. Без точного расчета магнитной системы невозможно создание эффективного электродвигателя или надежного привода.

Исторически развитие теории магнитных цепей неразрывно связано с именами великих физиков XIX века. Основы были заложены Андре-Мари Ампером, открывшим магнитное действие тока, и Майклом Фарадеем, введшим понятие магнитного поля. Однако формализация расчета, аналогичная электрическим цепям (известная как закон Гопкинсона), была разработана позже, что позволило инженерам перейти от эмпирических наблюдений к точному математическому моделированию. В данной статье рассматриваются ключевые аспекты классификации, физические принципы и современные алгоритмы расчета разветвленных и неразветвленных магнитных цепей с учетом нелинейных свойств ферромагнетиков.

1. Классификация и элементы магнитных цепей

Основным функциональным элементом большинства электротехнических устройств является магнитная система. Для упрощения анализа и проектирования реальную физическую систему представляют в виде идеализированной модели — магнитной цепи.

Конструктивно магнитная цепь включает в себя следующие компоненты:

Источники магнитного поля (обычно это катушки с током или постоянные магниты).
Магнитопроводы — элементы из ферромагнитных материалов (сердечники, ярма), обладающие высокой магнитной проницаемостью.
Воздушные зазоры или слои неферромагнитных материалов, через которые замыкается магнитный поток.

Рисунок 1. Конфигурации магнитных цепей: а — неразветвленная; б — разветвленная

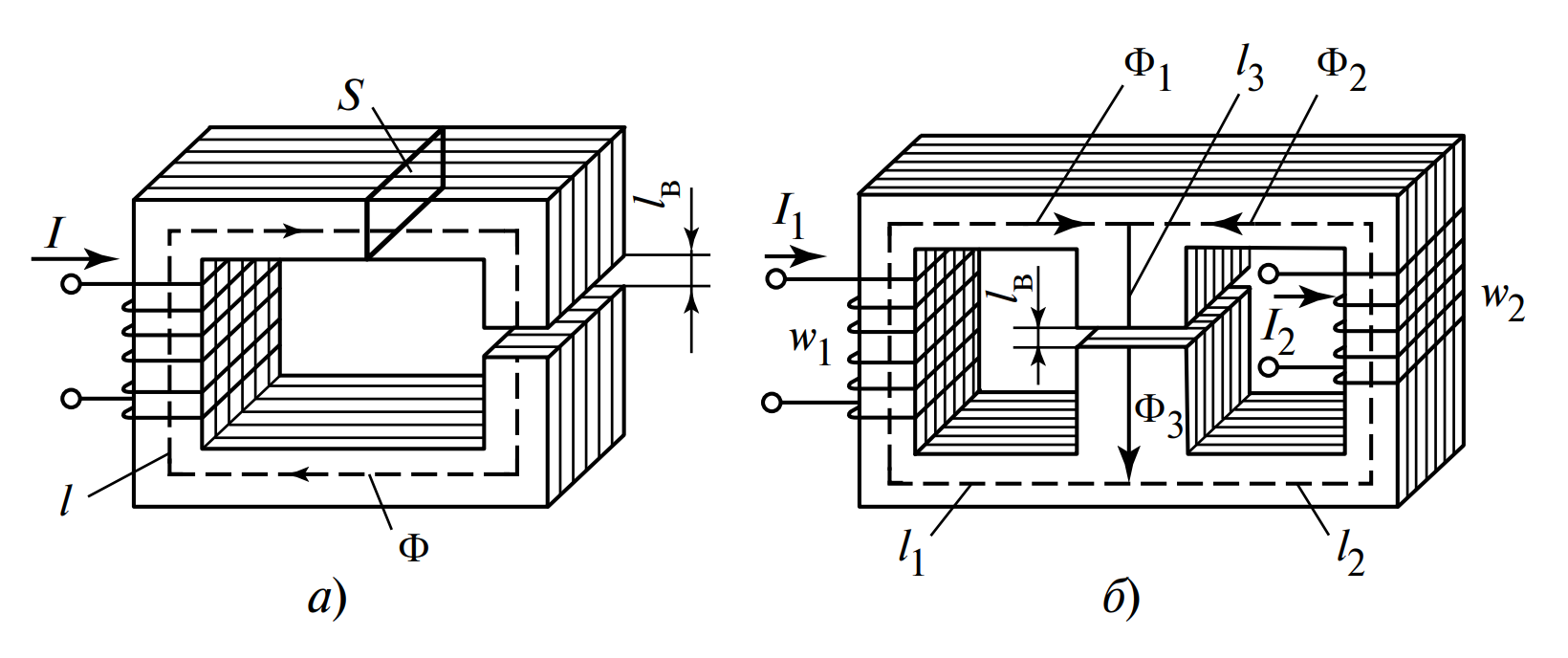
Рассмотрим принцип действия на примере электромагнита. Источником поля служит обмотка с количеством витков $ w $, по которой протекает электрический ток $ I $. Произведение тока на число витков создает магнитодвижущую силу (МДС):

$$ F = Iw $$

Единицей измерения МДС в системе СИ является ампер (А).

Метод аналогий: Для лучшего понимания процессов полезно проводить параллель с электрическими цепями. Магнитопровод выполняет функцию проводов (проводников), а воздушный зазор выступает в роли нагрузки (сопротивления), где формируется рабочее поле.

По топологии магнитные цепи делятся на два больших класса:

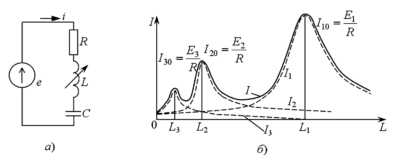
Неразветвленные (Рис. 1, а) — магнитный поток одинаков во всех сечениях цепи.
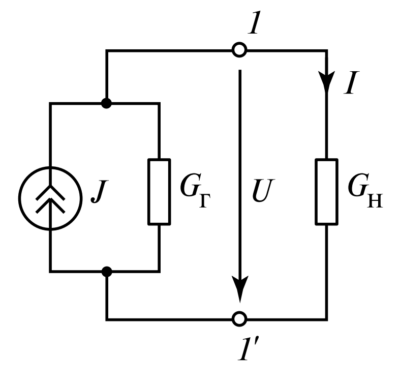
Разветвленные (Рис. 1, б) — поток разделяется на несколько ветвей, аналогично току в параллельных электрических ветвях.

Эквивалентные схемы замещения

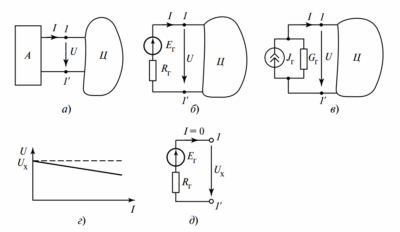
Для математического анализа физическую конструкцию заменяют расчетной моделью — эквивалентной схемой (Рис. 2).

[Рисунок 2. Эквивалентные схемы замещения для цепей из Рис. 1: а) Последовательное соединение источника МДС и магнитных сопротивлений; б) Сложная схема с узлами и контурами]

Рисунок 2. Эквивалентные схемы магнитной цепи: а — для неразветвленной; б — для разветвленной

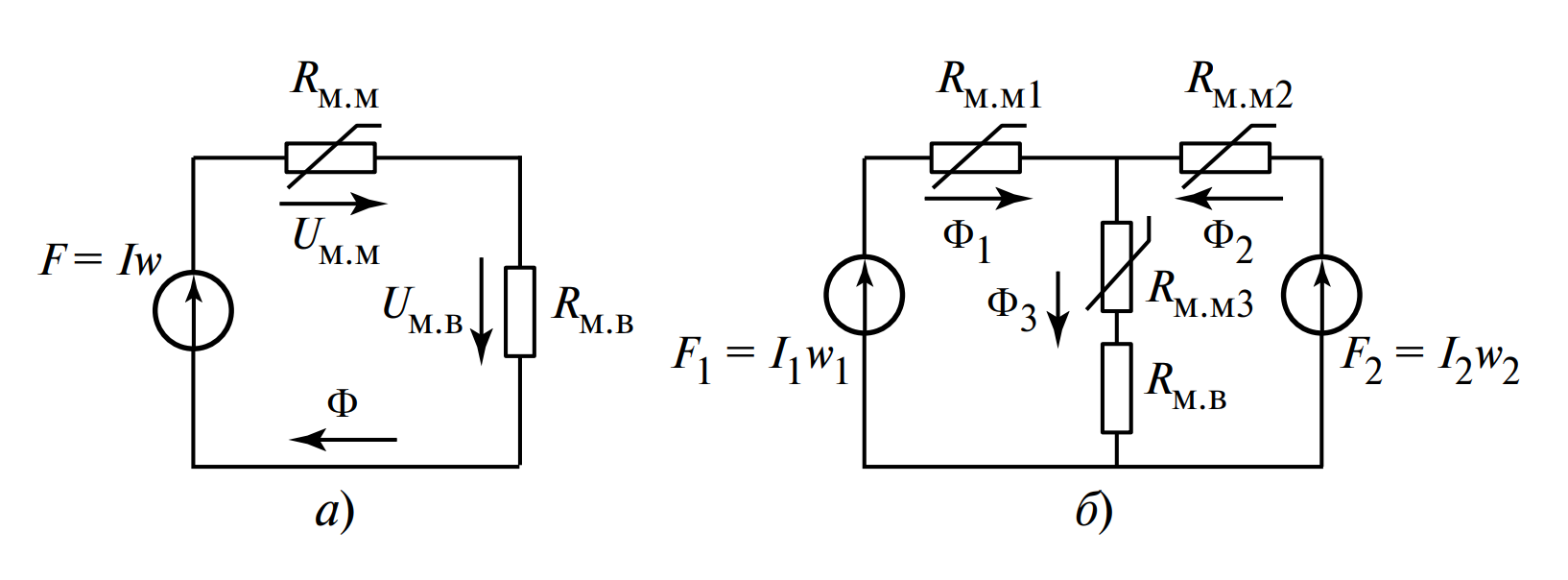
В этих схемах:

МДС $ F = Iw $ аналогична Электродвижущей силе (ЭДС).
Магнитный поток $ \Phi $ аналогичен электрическому току.
Магнитные сопротивления участков магнитопровода и зазора аналогичны электрическим резисторам.

Важно учитывать, что зависимость магнитной индукции $ B $ от напряженности поля $ H $ для ферромагнетиков нелинейна (кривая намагничивания), поэтому сопротивления магнитопровода на схемах отображаются как нелинейные элементы.

Допущения при инженерном расчете

Реальная физическая картина магнитного поля сложна: существуют потоки рассеяния $ \Phi_\sigma $ (замыкающиеся мимо целевого пути) и эффект «выпучивания» линий в зазоре. Для инженерных расчетов вводят ряд стандартных допущений:

Магнитная индукция $ B $ распределена равномерно по сечению магнитопровода.
Потоками рассеяния $ \Phi_\sigma $ пренебрегают (считаем, что весь поток идет по стали и зазору).
Выпучивание поля в зазоре не учитывается (площадь поля в зазоре равна площади сечения полюса).
Для расчета берется средняя линия магнитной индукции (геометрическая ось стержней и ярм).

2. Методика расчета неразветвленной магнитной цепи

Расчет базируется на Законе полного тока (интегральная форма уравнений Максвелла для стационарного поля). Задача обычно сводится к двум типам: нахождение необходимой МДС для создания заданного потока или определение потока при известной МДС.

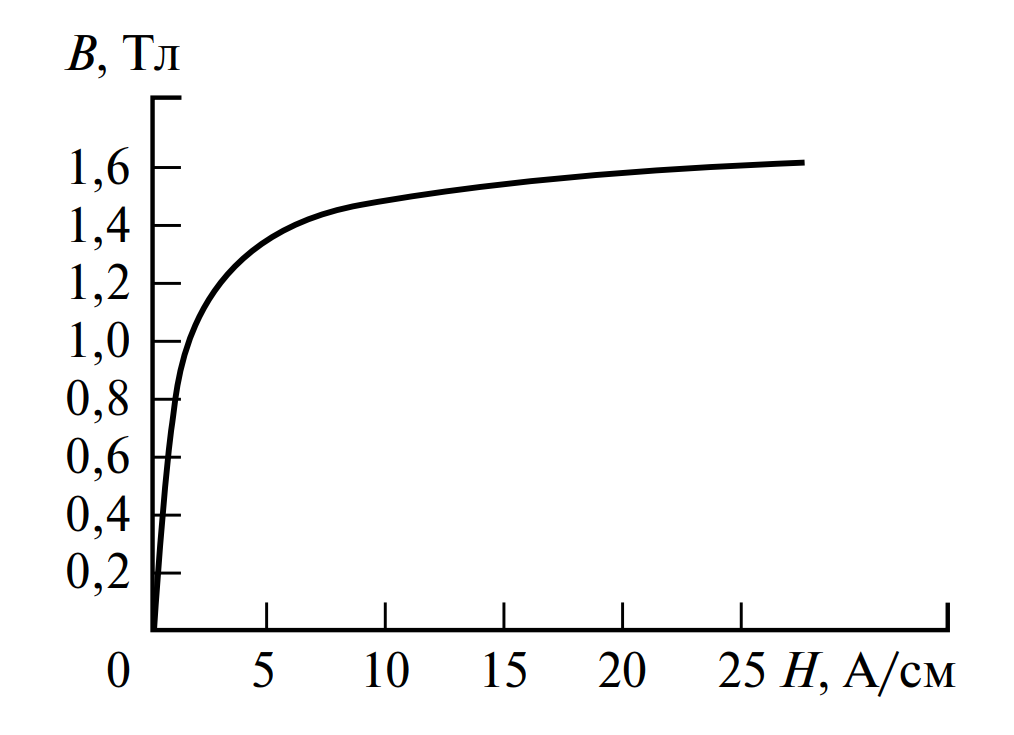
Рассмотрим схему на Рис. 1, а. Пусть заданы: $ l $ — средняя длина пути в стали, $ l_в $ — длина воздушного зазора, $ S $ — площадь поперечного сечения. Материал описывается кривой намагничивания (Рис. 3).

Рисунок 3. Типовая кривая намагничивания электротехнической стали 10880

Согласно закону полного тока, сумма падений магнитных напряжений вдоль контура равна суммарной МДС:

$$ Iw = Hl + H_в l_в = U_{м.м} + U_{м.в} $$

Где:

$ H $ и $ H_в $ — напряженности поля в стали и воздухе соответственно;

$ U_{м.м} $ — магнитное напряжение на участке ферромагнетика;

$ U_{м.в} $ — магнитное напряжение на воздушном зазоре.

Магнитное сопротивление

По аналогии с законом Ома $ R = l / (\gamma S) $, вводится понятие магнитного сопротивления:

$$ R_м = \frac{l}{\mu_r \mu_0 S} $$

Здесь $ \mu_0 = 4\pi \cdot 10^{-7} $ Гн/м — магнитная постоянная, а $ \mu_r $ — относительная магнитная проницаемость материала.
Поскольку $ \mu_r $ стали зависит от поля ($ \mu_r = f(\Phi) $), сопротивление стали $ R_{м.м} $ является величиной переменной. Однако сопротивление воздушного зазора $ R_{м.в} $ всегда линейно, так как для воздуха $ \mu_r \approx 1 $.

Уравнение состояния цепи приобретает вид:

$$ Iw = U_{м.м}(\Phi) + R_{м.в} \Phi $$

Графоаналитический метод решения

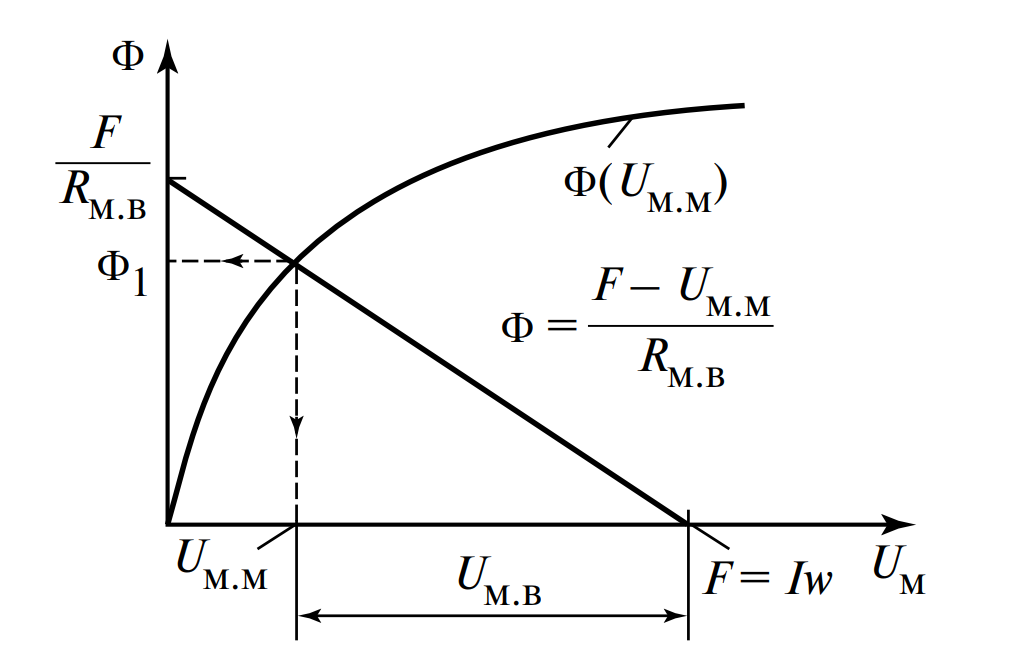
Из-за нелинейности слагаемого $ U_{м.м}(\Phi) $ аналитическое решение затруднено. Применяется графический метод (Рис. 4):

Строится вебер-амперная характеристика магнитопровода $ \Phi(U_{м.м}) $ путем пересчета кривой $ B(H) $ (умножением $ B $ на $ S $ и $ H $ на $ l $).
Строится линейная характеристика зазора $ \Phi(U_{м.в}) $, проходящая через начало координат.
Характеристики суммируются по оси напряжений для получения общей кривой $ \Phi(U_{м.м} + U_{м.в}) $.

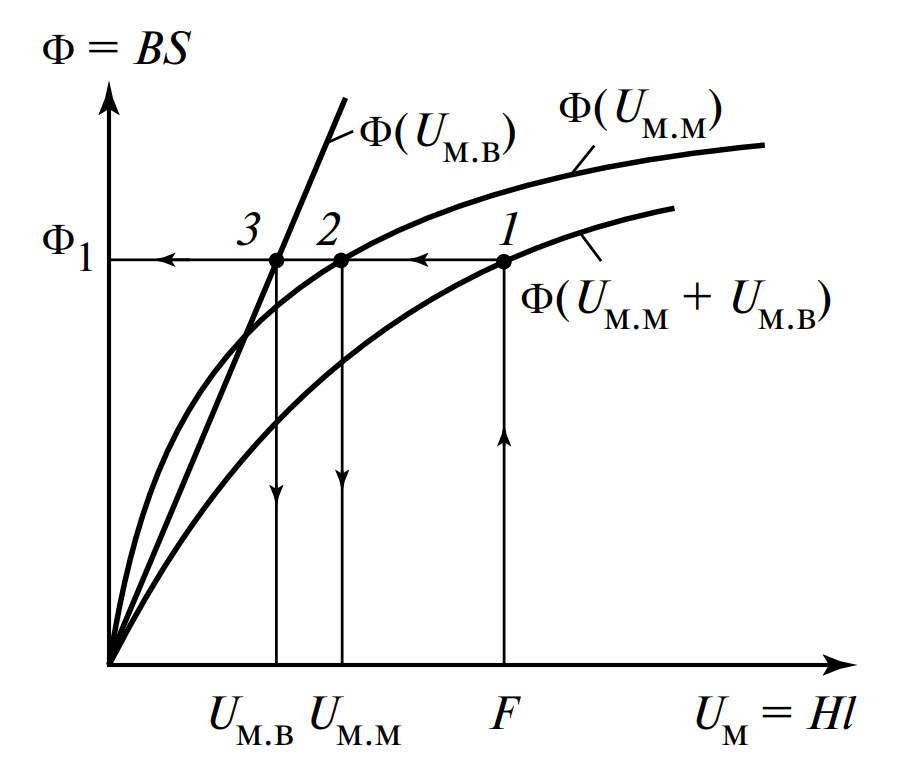
Рисунок 4. Графический расчет неразветвленной магнитной цепи

Алгоритм поиска рабочей точки:

Если задана МДС $ F $, откладываем её на оси абсцисс, восстанавливаем перпендикуляр до пересечения с суммарной кривой (точка 1). Проекция на ось ординат дает искомый поток $ \Phi_1 $.

3. Прямая и обратная задачи расчета

В инженерной практике выделяют два основных типа задач. Они различаются исходными данными и искомыми величинами.

Сравнение типов задач расчета магнитных цепей
Тип задачи	Дано (Известные параметры)	Найти (Искомые параметры)	Метод решения
Прямая задача	Геометрия, Материал (кривая B-H), Магнитный поток $ \Phi $ (или индукция B)	Необходимая МДС ($ Iw $) или ток $ I $	Аналитический (по формулам и таблицам), однозначное решение
Обратная задача	Геометрия, Материал (кривая B-H), МДС ($ Iw $)	Магнитный поток $ \Phi $ и индукция B в зазоре	Графоаналитический или итерационный (метод последовательных приближений)

Особенности решения обратной задачи методом итераций

Обратная задача сложнее, так как мы не знаем, в какой точке кривой намагничивания работаем, а значит, не знаем $ \mu_r $. Решение выполняется методом подбора (интерполяции):

Шаг 1. Задаемся начальным приближением потока $ \Phi_1 $. Обычно полагают, что всё падение напряжения приходится на зазор: $ \Phi_1 \approx \mu_0 H_в S $, где $ H_в l_в \approx Iw $. Это значение будет завышенным.
Шаг 2. Выбираем значение потока $ \Phi_2 < \Phi_1 $.
Шаг 3. Для обоих значений потока решаем прямую задачу: находим расчетные $ F_1 $ и $ F_2 $.
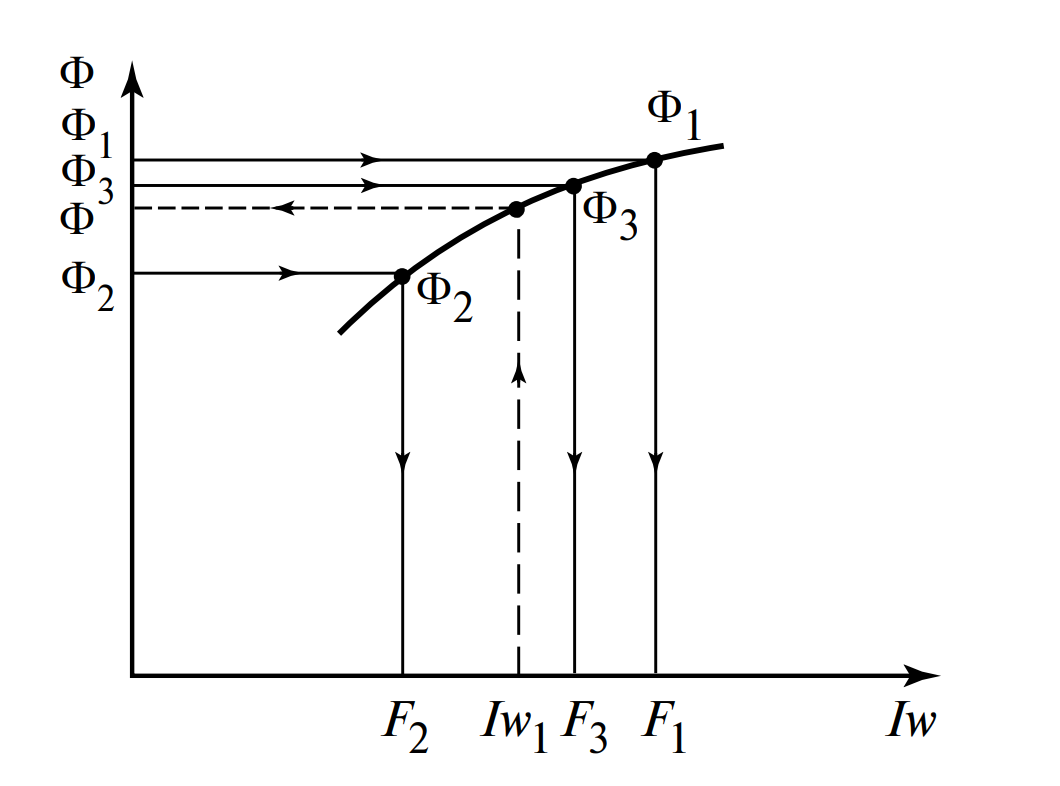
Шаг 4. Сравниваем полученные $ F $ с заданным. Строим локальный участок зависимости $ \Phi(Iw) $ (Рис. 6) и находим истинный поток, соответствующий заданному $ Iw $.

Рисунок 6. Графическая интерполяция при решении обратной задачи

4. Расчет разветвленной магнитной цепи

Для сложных систем (например, трехстержневой трансформатор или двигатель) применяются законы Кирхгофа для магнитных цепей:

Первый закон Кирхгофа (Принцип непрерывности потока): Алгебраическая сумма магнитных потоков в узле равна нулю.

$$ \sum \Phi = 0 \quad \Rightarrow \quad \Phi_1 + \Phi_2 — \Phi_3 = 0 $$

Второй закон Кирхгофа (Закон полного тока для контура): Алгебраическая сумма падений магнитных напряжений вдоль замкнутого контура равна алгебраической сумме МДС в этом контуре.

$$ \sum Hl = \sum Iw $$

Для схемы на Рис. 1,б система уравнений будет выглядеть так:

$$
\begin{cases}
\Phi_1 + \Phi_2 — \Phi_3 = 0 \\
I_1 w_1 = H_1 l_1 + H_3 l_3 + H_в l_в \\
I_2 w_2 = H_2 l_2 + H_3 l_3 + H_в l_в
\end{cases}
$$

Расчет удобно вести в табличной форме, последовательно вычисляя индукции и напряженности для каждого участка.

5. Практические примеры расчета

Пример 1: Расчет обмотки электромагнита (Прямая задача)

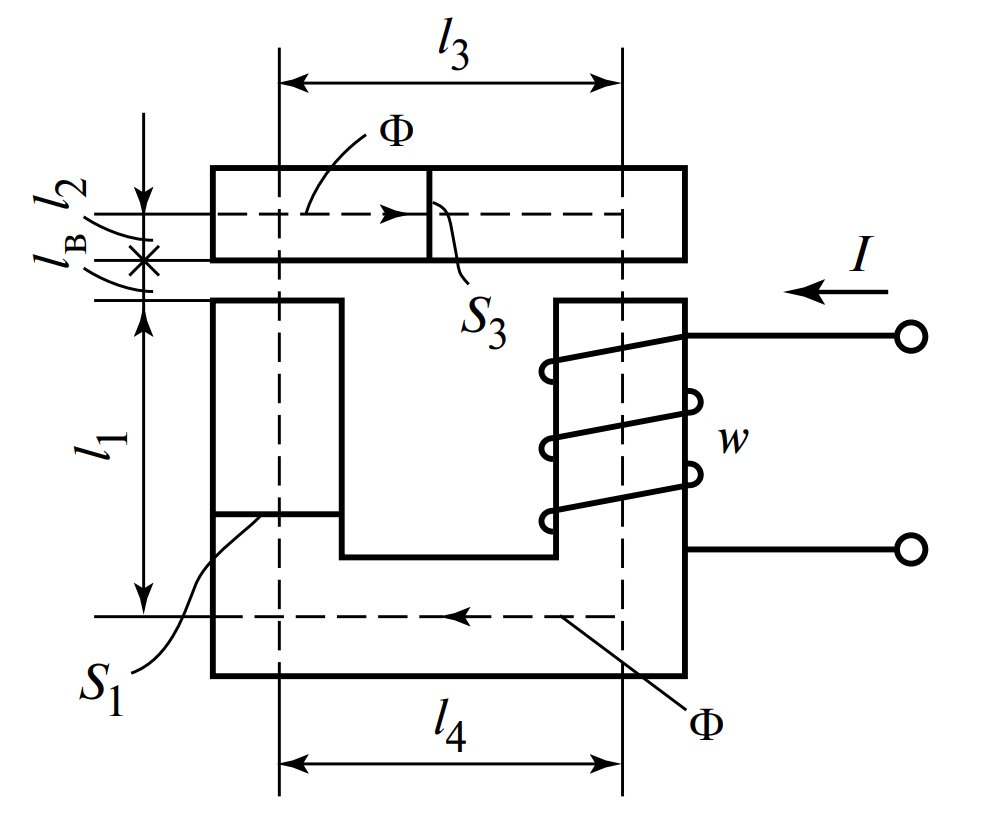
Дано: Электромагнит (Рис. 7) из стали 10880.

Ток $ I = 20 $ А. Требуемый поток $ \Phi = 30 \cdot 10^{-4} $ Вб.

Размеры: $ l_1 = 30 $ см, $ l_2 = 2,5 $ см, $ l_3 = l_4 = 12 $ см, зазор $ l_в = 0,5 $ см.

Сечения: $ S_1 = 30 $ см$^2$, $ S_3 = 25 $ см$^2$.

Найти: Число витков $ w $.

Рисунок 7. Конструктивная схема электромагнита

Решение:

Находим индукции на участках.Для ярма (участок 1 и 4): $ B_1 = B_4 = \Phi / S_1 = 30 \cdot 10^{-4} / (30 \cdot 10^{-4}) = 1 $ Тл.Для якоря (участок 3) и полюсов (участок 2): $ B_3 = B_2 = \Phi / S_3 = 30 \cdot 10^{-4} / (25 \cdot 10^{-4}) = 1.2 $ Тл.Индукция в зазоре $ B_в = B_3 = 1.2 $ Тл (без учета рассеяния).
Определяем напряженности поля $ H $ по кривой намагничивания (Рис. 3) для стали 10880:При $ B_1 = 1 $ Тл $\rightarrow H_1 = 150 $ А/м.При $ B_3 = 1.2 $ Тл $\rightarrow H_3 = 275 $ А/м.
Рассчитываем напряженность в воздушном зазоре:
$$ H_в = \frac{B_в}{\mu_0} = \frac{1.2}{4\pi \cdot 10^{-7}} \approx 9.55 \cdot 10^5 \text{ А/м (в примере использовано округление } 8 \cdot 10^5 \text{ для учебных целей)} $$
Примечание: В оригинальном тексте задачи приведено значение $ 8 \cdot 10^5 $, используем его для сохранения логики примера.
Составляем уравнение по закону полного тока:
$$ Iw = H_1(2l_1 + l_4) + H_в \cdot 2l_в + H_3(2l_2 + l_3) $$
Подставляем значения (переводя сантиметры в метры):
$$ Iw = 150(0.72) + 8 \cdot 10^5 (0.01) + 275(0.17) = 108 + 8000 + 46.75 \approx 8154.75 \text{ А} $$
Находим число витков:
$$ w = \frac{Iw}{I} = \frac{8154.75}{20} \approx 408 \text{ витков} $$

Пример 2: Изменение тока (Обратная задача)

Вопрос: Как изменится индукция в зазоре, если ток увеличить на 30% (до $ I’ = 26 $ А)?

Новая МДС: $ F’ = 8154.75 \cdot 1.3 \approx 10601 $ А.

Решение:

Поскольку зависимость $ B(H) $ нелинейна, нельзя просто увеличить поток на 30%. Используем метод итераций.

Мы знаем точку 1: при $ \Phi = 30 \cdot 10^{-4} $ Вб, $ F = 8155 $ А.

Зададимся большим потоком $ \Phi’ = 40 \cdot 10^{-4} $ Вб.

Пересчитываем индукции: $ B’_1 = 1.33 $ Тл, $ B’_3 = 1.6 $ Тл.

По кривой находим новые $ H $: $ H’_1 \approx 375 $ А/м, $ H’_3 \approx 2500 $ А/м.

Считаем новую МДС для этого потока: $ F_{расч} \approx 11220 $ А.

Видим, что $ 11220 > 10601 $ (наша имеющаяся МДС). Значит, истинный поток лежит между $ 30 \cdot 10^{-4} $ и $ 40 \cdot 10^{-4} $.
Строим график (Рис. 8) по полученным точкам и находим пересечение с уровнем $ F = 10601 $ А.

Результат графической интерполяции: $ \Phi_{ист} \approx 38 \cdot 10^{-4} $ Вб.

Рисунок 8. Решение обратной задачи методом интерполяции

Преимущества и недостатки методов расчета

Метод	Преимущества	Недостатки
Графоаналитический	Наглядность, физическая прозрачность процесса, не требует сложного ПО.	Низкая точность построения, трудоемкость при большом количестве итераций.
Численный (компьютерное моделирование)	Высокая точность, учет потоков рассеяния и геометрии (FEM-анализ), быстрота.	Требует специализированного ПО и точных моделей материалов, «черный ящик» для понимания сути процесса.

Интересные факты о магнитных цепях

1. Магнитное насыщение: Все ферромагнетики имеют предел намагничивания. Выше определенной точки (обычно 2.0-2.2 Тл для электротехнической стали) материал ведет себя как воздух, и дальнейшее увеличение тока становится энергетически невыгодным.
2. Гистерезис: При перемагничивании часть энергии тратится на нагрев сердечника. Площадь петли гистерезиса пропорциональна потерям энергии за один цикл.
3. «Магнитный изолятор»: В природе не существует идеальных магнитных изоляторов (подобных диэлектрикам для тока). Магнитное поле проникает через любые материалы, хотя сверхпроводники могут вытеснять его (эффект Мейснера).
4. Шихтование сердечников: Магнитопроводы двигателей делают не сплошными, а из тонких изолированных листов стали. Это нужно для борьбы с вихревыми токами (токами Фуко), которые иначе расплавили бы металл.
5. Пермаллой: Существуют сплавы (железо-никель), которые намагничиваются даже от слабого магнитного поля Земли. Они используются в высокоточных датчиках.
6. Миф о блокировке поля (Как работает экранирование): Вопреки расхожему мнению, магнитные экраны не «останавливают» и не «блокируют» магнитное поле. Они работают как «магнитные проводники» с экстремально низким сопротивлением. Поскольку магнитный поток всегда идет по пути наименьшего сопротивления, силовые линии концентрируются внутри материала экрана и огибают защищаемое пространство, подобно тому как вода обтекает камень в реке.
7. Невозможность разрыва цепи (Отсутствие монополей): В отличие от электрической цепи, где можно накопить заряд одного знака (плюс или минус), в магнитной цепи невозможно получить изолированный полюс (монополь). Если распилить магнит или сердечник пополам, вы не отделите Север от Юга, а получите два независимых магнита, каждый со своими полюсами. Это следствие уравнения Максвелла ($ \nabla \cdot \mathbf{B} = 0 $), которое гласит, что линии магнитного поля всегда замкнуты и не имеют начала и конца.

FAQ: Часто задаваемые вопросы

1. Зачем специально делают воздушный зазор в дросселях?

Воздушный зазор вводится для предотвращения магнитного насыщения сердечника при больших постоянных токах. Он «линеаризует» характеристику дросселя и стабилизирует индуктивность.

2. Можно ли использовать закон Ома для магнитных цепей?

Да, формально закон Гопкинсона ($ \Phi = F / R_м $) является полным аналогом закона Ома. Однако, в отличие от электрического сопротивления, магнитное сопротивление $ R_м $ не является константой и меняется в зависимости от величины поля.

3. Что такое потоки рассеяния и когда ими нельзя пренебрегать?

Это часть магнитного потока, которая замыкается через воздух, минуя рабочий зазор. Ими нельзя пренебрегать в точных расчетах трансформаторов и электрических машин, так как они влияют на реактивное сопротивление обмоток.

4. Почему гудят трансформаторы?

Основная причина — магнитострикция. Это явление изменения геометрических размеров ферромагнетика при его намагничивании. Сердечник буквально сжимается и разжимается с частотой сети (обычно 100 Гц для сети 50 Гц).

5. Как влияет температура на магнитную цепь?

При нагреве магнитная проницаемость ферромагнетиков падает. При достижении точки Кюри (для железа около 770°C) ферромагнитные свойства исчезают полностью, и материал становится парамагнетиком.

Заключение

Расчет магнитных цепей является критически важным этапом проектирования электротехнических устройств. Несмотря на кажущуюся простоту аналогии с электрическими цепями, наличие нелинейных ферромагнитных элементов требует применения специфических методов анализа — от графоаналитических построений до сложных итерационных алгоритмов. Понимание физики процессов в стали и воздушном зазоре позволяет инженерам создавать эффективные, экономичные и мощные электрические машины, которые являются движущей силой современной промышленности.

Нормативные документы:

ГОСТ 32482-2013 — Сталь электротехническая холоднокатаная анизотропная тонколистовая. Технические условия.
ГОСТ Р 52002-2003 — Электротехника. Основные понятия. Термины и определения.
ГОСТ 2.701-2008 — ЕСКД. Схемы. Виды и типы. Общие требования к выполнению.

Магнитные цепи: Теоретические основы, классификация и методики расчета