Содержание страницы
- Линейные диаграммы: основы и применение
- Круговые диаграммы: теоретические основы
- Пример 1: Анализ последовательной цепи с переменной емкостью
- Пример 2: Анализ параллельной цепи (поиск минимального тока)
- Сравнительный анализ и области применения
- Интересные факты о диаграммах в теории цепей
- Часто задаваемые вопросы (FAQ)
- Заключение
Примечание: Термин «годограф» (от греч. ὁδός — путь, γράφω — пишу) буквально означает «описание пути». В электротехнике это траектория, которую описывает конец вектора (фазора) тока или напряжения при изменении какого-либо параметра цепи или частоты.
Линейные диаграммы: основы и применение
Линейные диаграммы являются наиболее простым случаем. В общем случае они получаются при суммировании векторов, когда у одного из векторов изменяется только модуль, а фаза остается постоянной. Классическое уравнение для линейной диаграммы имеет вид (см. рис. 1а):
\[ \dot{I} = \dot{I}_1 + k \cdot \dot{I}_2 \]
где:
- \(\dot{I}\) — итоговый вектор (например, суммарный ток);
- \(\dot{I}_1\) — постоянный вектор (неизменный по модулю и фазе);
- \(\dot{I}_2\) — постоянный по фазе, но не по модулю вектор (опорный вектор);
- \(k\) — переменный действительный коэффициент (\(k = \text{varia}\)), например, коэффициент трансформации или передаточная функция реостата.
Геометрически это выглядит следующим образом: вектор \(\dot{I}_1\) откладывается из начала координат. К его концу прибавляется вектор \(k \cdot \dot{I}_2\). Поскольку \(\dot{I}_2\) имеет постоянное направление, при изменении \(k\) (например, от 0 до \(\infty\)) конец вектора \(k \cdot \dot{I}_2\) будет двигаться по прямой линии, исходящей из конца вектора \(\dot{I}_1\). Соответственно, конец результирующего вектора \(\dot{I}\) также будет описывать прямую линию.
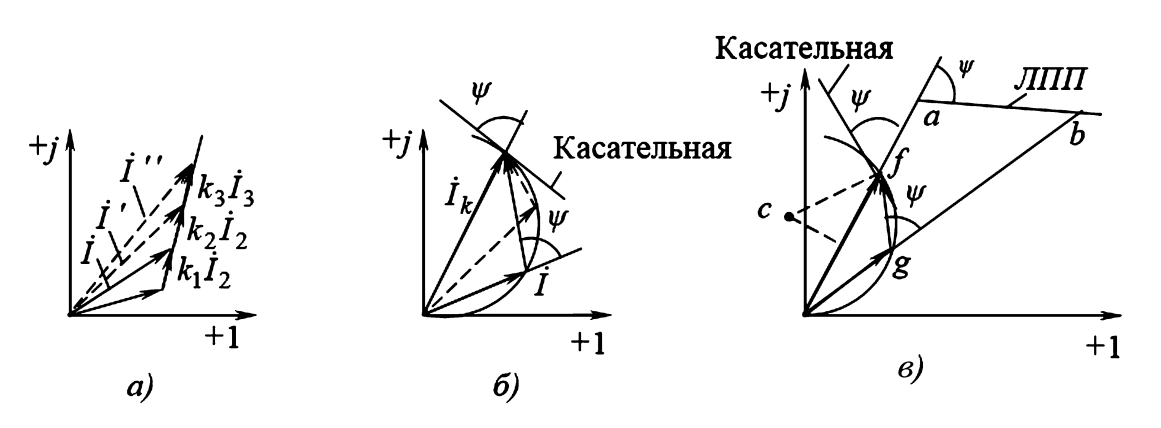
Рис. 1. Линейные и круговые диаграммы: а — линейная диаграмма; б — круговая диаграмма; в — общий случай построения круговой диаграммы.
Круговые диаграммы: теоретические основы
Круговые диаграммы — значительно более распространенный и мощный инструмент анализа. Они возникают в случаях, когда исследуемая величина (например, ток \(\dot{I}\)) является дробно-линейной функцией переменного параметра. Классический случай — цепь, состоящая из постоянного комплексного сопротивления \(Z_1\) и переменного сопротивления \(k \cdot Z_2\), подключенная к источнику ЭДС \(\dot{E}\):
\[ \dot{I} = \frac{\dot{E}}{Z_1 + k \cdot Z_2} \]
Здесь \(Z_1\) и \(Z_2\) — комплексные импедансы, а \(k\) — переменный действительный параметр (например, \(k = R\), или \(k = X_L\), или \(k = X_C\)).
Обратная величина тока, то есть полная проводимость, в этом случае является линейной функцией:
\[ \frac{1}{\dot{I}} = \frac{Z_1 + k \cdot Z_2}{\dot{E}} = \frac{Z_1}{\dot{E}} + k \cdot \frac{Z_2}{\dot{E}} \]
Годографом величины \((1/\dot{I})\) является прямая линия (аналогично линейной диаграмме). В комплексном анализе преобразование вида \(w = 1/z\) (инверсия) отображает прямую линию в окружность, проходящую через начало координат. Таким образом, годограф тока \(\dot{I}\) будет являться окружностью.
Геометрическая интерпретация
Исходное уравнение \(\dot{I}(Z_1 + k \cdot Z_2) = \dot{E}\) можно преобразовать. Разделим его на \(Z_1\):
\[ \dot{I} + k \cdot \dot{I} \cdot \left(\frac{Z_2}{Z_1}\right) = \frac{\dot{E}}{Z_1} \]
Введем обозначения:
- \(\dot{I}_k = \dot{E} / Z_1\) — постоянный вектор тока (ток при \(k=0\)).
- \(Z_1 = |Z_1|e^{j\phi_1}\) и \(Z_2 = |Z_2|e^{j\phi_2}\)
- \(\frac{Z_2}{Z_1} = \frac{|Z_2|}{|Z_1|} e^{j(\phi_2 — \phi_1)} = \frac{|Z_2|}{|Z_1|} e^{j\psi}\), где \(\psi = \phi_2 — \phi_1\) — постоянный угол, равный разности фаз комплексных сопротивлений.
Текст исходного материала для упрощения приводит уравнение к виду (объединяя \(k\) и \(\frac{|Z_2|}{|Z_1|}\) в один переменный параметр, который мы также обозначим \(k\)):
\[ \dot{I} + k \cdot \dot{I} e^{j\psi} = \dot{I}_k \]
На комплексной плоскости (рис. 1б) это уравнение представляет собой треугольник векторов \(0gf\), у которого:
- Одна сторона (\(0f\)) — постоянный вектор \(\dot{I}_k\).
- Две другие стороны (\(0g = \dot{I}\) и \(gf = k \cdot \dot{I} e^{j\psi}\)) — изменяются при изменении \(k\).
При этом угол между векторами \(\dot{I}\) и \(k \cdot \dot{I} e^{j\psi}\) (если их отложить из одной точки) остается постоянным и равным \(\psi\). Следовательно, угол при вершине \(g\) в треугольнике \(0gf\) (\(\angle 0gf\)) также постоянен и равен \((180^\circ — \psi)\). Из геометрии известно, что геометрическим местом вершин \(g\) такого треугольника, построенного на фиксированном основании \(0f\), является окружность, проходящая через точки 0 и \(f\).
Пошаговый алгоритм построения круговой диаграммы
Для построения этой окружности (рис. 1в) используется свойство равенства угла \(\psi\) (между векторами \(\dot{I}\) и \(k\dot{I}e^{j\psi}\)) и угла между хордой \(\dot{I}_k\) (отрезок \(0f\)) и касательной к окружности в точке \(f\).
- Выбор масштабов и построение базисного вектора. Выбирают масштаб токов \(m_I\) (А/см) и откладывают из начала координат (точки 0) вектор \(\dot{I}_k\). Он образует хорду \(0f\) будущей окружности.
- Определение касательной. Продолжают хорду \(0f\) за точку \(f\) и от этой линии откладывают угол \(\psi\). Полученная линия является касательной к окружности в точке \(f\).
- Нахождение центра окружности (точка c). Проводят перпендикуляр к касательной в точке \(f\). Затем находят середину хорды \(0f\) и восстанавливают из нее перпендикуляр. Пересечение этих двух перпендикуляров определяет центр окружности \(c\).
- Построение дуги (годографа). Проводят дугу окружности с центром \(c\) и радиусом \(R = |c0| = |cf|\). По этой дуге будет перемещаться конец искомого вектора \(\dot{I}\) (вектор \(0g\)) при изменении параметра \(k\).
Примечание: Угол \(\psi = \phi_2 — \phi_1\) является ключевым параметром.
- Если \(\psi = 0\) (оба импеданса чисто активные), годограф вырождается в прямую.
- Если \(\psi = \pm 90^\circ\) (один чисто активный, другой чисто реактивный), хорда \(\dot{I}_k\) становится диаметром окружности (что упрощает построение, как в Примере 2).
Физически параметр \(k\) (например, сопротивление) обычно изменяется от 0 до \(\infty\), поэтому годографом тока является не вся окружность, а только ее дуга.
Определение переменного параметра (Линия ЛПП)
Диаграмма не только показывает, как меняется ток, но и позволяет определить, какому значению переменного параметра (\(k_1 \cdot Z_2\)) соответствует каждая точка \(g\) на окружности. Для этого используется линия переменного параметра (ЛПП) (рис. 1в).
- Выбирают масштаб сопротивлений \(m_z\) (Ом/см).
- На векторе \(\dot{I}_k\) (или на его продолжении) от начала координат откладывают отрезок \(oa\), изображающий постоянное сопротивление \(Z_1\): \(|oa| = |Z_1| / m_z\).
- Из точки \(a\) проводят линию (ЛПП) под углом \(-\psi\) к направлению вектора \(0a\).
Теперь, чтобы определить параметр, соответствующий току \(\dot{I}\) (вектор \(0g\)), продолжают вектор \(0g\) до пересечения с ЛПП в точке \(b\). Длина получившегося отрезка \(ab\) изображает переменный параметр в том же масштабе \(m_z\).
Доказывается это из подобия треугольников \(0gf\) и \(0ab\). Они имеют общий угол \(\angle fog\), а также \(\angle ogf = \angle oab = 180^\circ — \psi\). Из подобия следует:
\[ \frac{ab}{gf} = \frac{oa}{og} \implies ab = \frac{gf}{og} \cdot oa \]
Отрезки \(og\) и \(gf\) изображают токи \(\dot{I}\) и \(k \cdot \dot{I} e^{j\psi}\). В соответствии с исходным уравнением \(\dot{I} + k \cdot \dot{I} \cdot (Z_2/Z_1) = \dot{I}_k\), отношение модулей \(\frac{|gf|}{|og|} = k \cdot \frac{|Z_2|}{|Z_1|}\). (В тексте примера \(k_1\) — это \(k\), а \(Z_2\) — это \(Z_2/Z_1\). Будем придерживаться обозначений \(k_1 \cdot Z_2\), где \(k_1\) — переменный параметр, а \(Z_2\) — импеданс, к которому он относится.)
Подставляя \(oa = |Z_1|/m_z\) и \(\frac{|gf|}{|og|} = \frac{k_1 \cdot |Z_2|}{|Z_1|}\), получим:
\[ ab = \left( \frac{k_1 \cdot |Z_2|}{|Z_1|} \right) \cdot \left( \frac{|Z_1|}{m_z} \right) = \frac{k_1 \cdot |Z_2|}{m_z} \]
Иными словами, отрезок \(ab\), умноженный на масштаб сопротивления \(m_z\), изображает изменяющееся сопротивление \(k_1 \cdot Z_2\):
\[ k_1 \cdot |Z_2| = |ab| \cdot m_z \]
Возможна и обратная задача: откладывая на ЛПП различные значения \(k_1 \cdot |Z_2|\) (в виде отрезков \(ab\)), можно соединять концы этих отрезков (точки \(b\)) с точкой \(0\) и на пересечении с окружностью (в точках \(g\)) определять величины искомых токов \(\dot{I}\) (векторы \(0g\)).
Пример 1: Анализ последовательной цепи с переменной емкостью
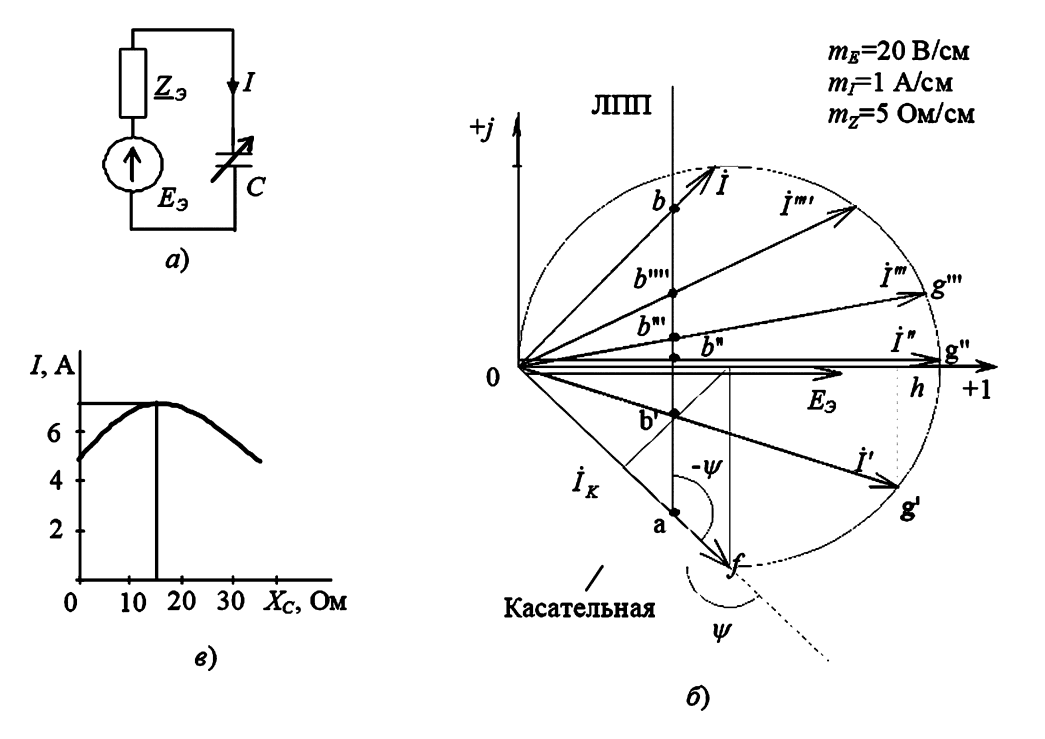
Рис. 2. Исследование последовательной цепи: а — схема цепи; б — круговая диаграмма; в — зависимость тока цепи от емкостного сопротивления.
Задача: В одной из ветвей электрической цепи изменяется емкость \(C\). Вся цепь, кроме емкости \(C\), заменена эквивалентным генератором (по теореме об эквивалентном генераторе, или теореме Тевенена). С помощью круговой диаграммы определить токи для различных величин \(C\) и построить график зависимости тока от емкости. Параметры эквивалентного генератора (рис. 2а) равны: \(\dot{E}_Э = 100 \text{ В}\) (фазу примем за 0°), \(Z_Э = 20e^{j45^\circ} \text{ Ом}\).
Решение:
1. Теоретическое обоснование. В соответствии со схемой на рисунке 2а, ток в цепи определяется по закону Ома для полной цепи:
\[ \dot{I} = \frac{\dot{E}_Э}{Z_Э + Z_C} = \frac{\dot{E}_Э}{Z_Э — jX_C} \]
Это уравнение полностью соответствует каноническому виду \( \dot{I} = \dot{E} / (Z_1 + k_1 Z_2) \), где:
- \(\dot{E} = \dot{E}_Э = 100 \angle 0^\circ \text{ В}\)
- \(Z_1 = Z_Э = 20 \angle 45^\circ \text{ Ом}\)
- \(Z_2 = -j = 1 \angle -90^\circ \text{ Ом}\)
- \(k_1 = X_C = \text{varia}\) (переменный параметр, \(\text{Ом}\))
2. Расчет параметров диаграммы.
- Базисный ток \(\dot{I}_k\) (при \(k_1 = X_C = 0\), т.е. \(C = \infty\)):
\[ \dot{I}_k = \frac{\dot{E}_Э}{Z_Э} = \frac{100 \angle 0^\circ}{20 \angle 45^\circ} = 5 \angle -45^\circ \text{ А} \] - Угол \(\psi\):
\[ \psi = \phi_2 — \phi_1 = (-90^\circ) — (45^\circ) = -135^\circ \]
3. Построение диаграммы (рис. 2б).
- Выбираем масштабы произвольно, но удобно: \(m_U = 20 \text{ В/см}\) и \(m_I = 1 \text{ А/см}\).
- На комплексной плоскости откладываем \(\dot{E}_Э\) по вещественной оси (для ориентира) и вектор базисного тока \(\dot{I}_k\) (хорда \(0f\)) длиной \(5 / m_I = 5 \text{ см}\) под углом \(-45^\circ\).
- На продолжении вектора \(\dot{I}_k\) за точку \(f\) откладываем угол \(\psi = -135^\circ\). Это положение касательной.
- Проводим перпендикуляр к касательной в точке \(f\) и перпендикуляр к середине хорды \(0f\). Их пересечение определяет центр окружности \(c\).
- Проводим дугу окружности через точки 0 и \(f\). По этой дуге будет перемещаться конец вектора \(\dot{I}\) при изменении емкости \(C\) (от 0 до \(\infty\)).
4. Построение Линии Переменного Параметра (ЛПП).
- На хорде \(0f\) отложим произвольной длины отрезок \(oa\). Например, \(|oa| = 4 \text{ см}\).
- Этот отрезок изображает сопротивление \(Z_Э\). Он определяет масштаб сопротивлений:
\[ m_z = \frac{|Z_Э|}{|oa|} = \frac{20 \text{ Ом}}{4 \text{ см}} = 5 \text{ Ом/см} \] - Под углом \(-\psi = -(-135^\circ) = +135^\circ\) к линии \(0a\) проводим из точки \(a\) Линию Переменного Параметра (ЛПП).
- На этой линии откладываем отрезки \(ab’\), \(ab»\), \(ab»’\) и т.д., изображающие сопротивления \(X_C\) в том же масштабе \(m_z\). (Например, для \(X_C = 10 \text{ Ом}\) отрезок \(ab’ = 10 / 5 = 2 \text{ см}\)).
5. Анализ и построение графика.
Проводим лучи из точки 0 через точки \(b’\), \(b»\), \(b»’\) до пересечения с окружностью в точках \(g’\), \(g»\), \(g»’\). Эти лучи (векторы \(0g’\), \(0g»\)) и есть векторы тока \(\dot{I}\) при соответствующих сопротивлениях \(X_C\). Измеряя отрезки \(|0g’|\), \(|0g»|\) и т.д. и умножая их на масштаб токов \(m_I\), определяем значения токов \(I\).
Строим график зависимости тока \(I\) от сопротивления \(X_C\) (рис. 2в). График имеет максимум при токе \(\dot{I}»\) (точка \(g»\)). На диаграмме (рис. 2б) видно, что этот вектор тока совпадает по фазе с напряжением \(\dot{E}_Э\), что свидетельствует о том, что в цепи наблюдается резонанс напряжений (при \(\text{Im}(Z_Э + Z_C) = 0\)).
6. Анализ мощностей.
Если спроектировать вектор тока (например, \(0g’\)) на вектор напряжения \(\dot{E}_Э\) (вещественная ось), то отрезок \(0h\) изобразит в масштабе токов \(I \cos\phi\) (активную составляющую тока). В масштабе мощностей \(m_P = m_U \cdot m_I = 20 \cdot 1 = 20 \text{ Вт/см}\) этот же отрезок \(0h\) изобразит активную мощность \(P = E_Э \cdot I \cos\phi\). Отрезок \(hg’\) (перпендикуляр) изобразит в том же масштабе \(m_P\) реактивную мощность \(Q = E_Э \cdot I \sin\phi\).
Пример 2: Анализ параллельной цепи (поиск минимального тока)
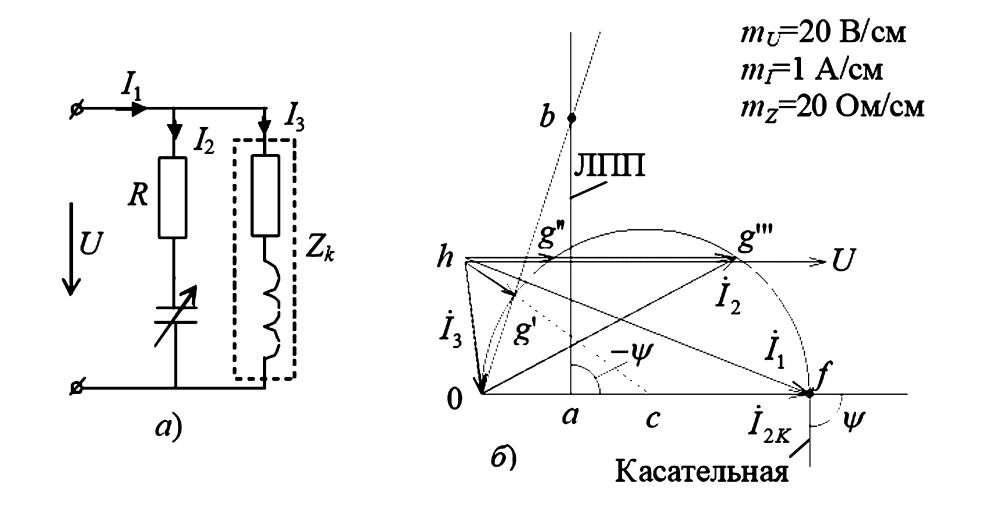
Рис. 3. Исследование параллельной цепи: а — схема цепи; б — круговая диаграмма.
Задача: Определить с помощью круговой диаграммы, при какой емкости \(C\) ток \(\dot{I}_1\) в неразветвленной части электрической цепи (рис. 3а) будет минимален. Известно, что при отсутствии емкости \(C\) (т.е. \(C=0 \implies X_C = \infty\)) токи имели следующие значения: \(I_1 = 7 \text{ А}\), \(I_2 = 6 \text{ А}\), \(I_3 = 2 \text{ А}\). Напряжение \(U = 120 \text{ В}\). Определить также токи при резонансе.
Примечание к задаче: В исходном тексте примера (и на рис. 3а) имеется логическая путаница в обозначениях. На схеме ток \(I_1\) показан как ток в неразветвленной части, расходящийся на \(I_2\) и \(I_3\), что означает \(\dot{I}_1 = \dot{I}_2 + \dot{I}_3\). Однако ход решения и построение диаграммы (рис. 3б) однозначно соответствуют уравнению \(\dot{I}_2 = \dot{I}_1 + \dot{I}_3\). Мы будем следовать построению на диаграмме, подразумевая, что \(\dot{I}_2\) — ток в ветви с (R, C), \(\dot{I}_3\) — ток в постоянной ветви, а \(\dot{I}_1\) — ток в другой постоянной ветви, и \(\dot{I}_2\) — их сумма. Либо (что более вероятно) \(\dot{I}_2\) — общий ток, а \(\dot{I}_1\) и \(\dot{I}_3\) — токи ветвей. Будем придерживаться построения, где \(\vec{0f} = \vec{0h} + \vec{hf}\), что соответствует \(\dot{I}_{2k} = \dot{I}_3 + \dot{I}_1(\text{init})\).
Решение:
1. Теоретическое обоснование. Примем КЗТ (согласно рис. 3а) \(\dot{I}_1 = \dot{I}_2 + \dot{I}_3\). Ветвь 3 постоянна, значит \(\dot{I}_3\) — постоянный вектор. Ветвь 2 изменяется (\(R\) и \(C\)), значит \(\dot{I}_2\) — переменный вектор. \(\dot{I}_1\) — искомый суммарный ток.
Ток \(\dot{I}_2\) изменяется в соответствии с уравнением:
\[ \dot{I}_2 = \frac{\dot{U}}{R — jX_C} \]
Это уравнение круговой диаграммы. Приведем его к каноническому виду \(\dot{I} + k\dot{I}e^{j\psi} = \dot{I}_k\).
\(\dot{I}_2 (R — jX_C) = \dot{U} \implies \dot{I}_2 R — j\dot{I}_2 X_C = \dot{U}\). Разделим на \(R\):
\[ \dot{I}_2 — j \frac{X_C}{R} \dot{I}_2 = \frac{\dot{U}}{R} \implies \dot{I}_2 + k \dot{I}_2 e^{j\psi} = \dot{I}_{2k} \]
где \(\dot{I}_{2k} = \dot{U}/R\), \(k = X_C/R\), \(\psi = -90^\circ\).
2. Построение диаграммы \(\dot{I}_2\).
Начальные данные «при отсутствии емкости C». Логично предположить, что \(C=0 \implies X_C = \infty\), тогда \(\dot{I}_2 = 0\). Но дано \(I_2 = 6 \text{ А}\). Вероятно, «отсутствие» означает \(C=\infty \implies X_C = 0\). Тогда \(\dot{I}_2(\text{init}) = \dot{U}/R = \dot{I}_{2k}\).
Примем это: \(I_{2k} = 6 \text{ А}\).
Строим круговую диаграмму тока \(\dot{I}_2\). Выбираем \(m_I = 1 \text{ А/см}\). Откладываем вектор \(\dot{U}\) по вещественной оси. Тогда \(\dot{I}_{2k} = \dot{U}/R\) также на вещественной оси.
Вектор \(\dot{I}_{2k}\) (хорда \(0f\)) имеет длину \(6/1 = 6 \text{ см}\).
Так как \(\psi = -90^\circ\), хорда \(0f\) является диаметром окружности. (Касательная в \(f\) идет под \(-90^\circ\), перпендикуляр к ней — сама линия \(0f\). Перпендикуляр к середине \(0f\) — вертикальная линия. Центр \(c\) лежит на \(0f\) в середине).
Проводим дугу окружности, по которой будет перемещаться конец вектора \(\dot{I}_2\).
3. Построение суммарного тока \(\dot{I}_1\).
По первому закону Кирхгофа \(\dot{I}_1 = \dot{I}_2 + \dot{I}_3\).
В начальном режиме (при \(X_C=0\)): \(\dot{I}_1(\text{init}) = \dot{I}_{2k} + \dot{I}_3\).
Мы знаем модули: \(|I_1(\text{init})| = 7 \text{ А}\), \(|I_2(\text{init})| = |I_{2k}| = 6 \text{ А}\), \(|I_3| = 2 \text{ А}\).
Строим треугольник токов (рис. 3б) для нахождения постоянного вектора \(\dot{I}_3\).
Из точки 0 (начало \(\dot{I}_{2k}\)) проводим дугу радиусом \(R_3 = |I_3|/m_I = 2/1 = 2 \text{ см}\).
Из точки \(f\) (конец \(\dot{I}_{2k}\)) проводим дугу радиусом \(R_1 = |I_1(\text{init})|/m_I = 7/1 = 7 \text{ см}\).
Внимание: Этап построения в исходном тексте соответствует \(\dot{I}_{2k} = \dot{I}_1 + \dot{I}_3\). Мы следуем этому построению. Пересечение дуг определяет точку \(h\). Вектор \(\vec{0h} = \dot{I}_3\). Вектор \(\vec{hf} = \dot{I}_1(\text{init})\). Векторная сумма \(\vec{0h} + \vec{hf} = \vec{0f}\) выполняется.
Теперь, когда \(C\) изменяется, \(\dot{I}_2\) движется по окружности (вектор \(\vec{0g’}\)).
Ток \(\dot{I}_1 = \dot{I}_2 — \dot{I}_3 = \vec{0g’} — \vec{0h} = \vec{hg’}\).
Таким образом, годографом тока \(\dot{I}_1\) являются отрезки, соединяющие постоянную точку \(h\) с точками \(g\) на окружности \(\dot{I}_2\).
4. Анализ диаграммы.
- Минимальный ток \(\dot{I}_1\): Это будет отрезок \(hg’\) минимальной длины. Минимальное значение \(|I_1|\) будет тогда, когда отрезок \(hg’\) направлен из точки \(h\) к центру окружности \(c\). (На рис. 3б показано пунктиром).
- Резонанс токов: Это режим, когда ток \(\dot{I}_1\) (в неразветвленной части) совпадает по фазе с напряжением \(\dot{U}\). Так как \(\dot{U}\) мы направили по вещественной оси (параллельно \(\dot{I}_{2k}\)), нам нужно найти на окружности такие точки \(g»\) и \(g»’\), чтобы вектор \(\vec{hg}\) был параллелен \(\vec{0f}\).
Проводим из точки \(h\) линию, параллельную \(\dot{U}\) (оси 0-f). Она пересекает окружность в двух точках: \(g»\) и \(g»’\). Это означает, что в данной цепи возможны два режима резонанса токов (при двух разных значениях \(C\)).
Измеряя эти отрезки, определяем значения токов при резонансе:
\(I_{1p}» = |hg»| \cdot m_I \approx 1.3 \text{ А}\)
\(I_{1p}»’ = |hg»’| \cdot m_I \approx 6 \text{ А}\)
Из диаграммы также видно, что минимальный ток \(I_1\) (вектор \(hg’\)) не совпадает по фазе с \(\dot{U}\), т.е. минимальный ток в цепи получается не при резонансе токов.
5. Определение емкости.
Строим ЛПП.
\(R = U/I_{2k} = 120 / 6 = 20 \text{ Ом}\).
Выберем \(m_z = 20 \text{ Ом/см}\).
На отрезке \(0f\) откладываем \(|oa| = R / m_z = 20 / 20 = 1 \text{ см}\).
Проводим ЛПП из \(a\) под углом \(-\psi = -(-90^\circ) = +90^\circ\) (вертикально вверх).
На этой ЛПП отрезки \(ab\) будут изображать сопротивления \(X_C\) (т.к. \(k = X_C/R\), \(ab \cdot m_z = k \cdot R = X_C\)).
Для определения \(X_C\), при котором ток \(I_1\) минимален, продолжаем вектор \(\dot{I}_2’\) (т.е. \(\vec{0g’}\)) до пересечения с ЛПП в точке \(b\).
Измеряем \(ab\). По данным примера, \(|ab| = 5 \text{ см}\).
Тогда \(X_C = |ab| \cdot m_z = 5 \cdot 20 = 100 \text{ Ом}\).
Емкость \(C\) (при \(\omega = 314 \text{ рад/с}\)):
\[ C = \frac{1}{\omega X_C} = \frac{1}{314 \cdot 100} \approx 31.8 \cdot 10^{-6} \text{ Ф} = 31.8 \text{ мкФ} \]
Таким образом, при \(C = 31.8 \text{ мкФ}\) ток в неразветвленной части цепи будет минимальным.
Сравнительный анализ и области применения
Линейные и круговые диаграммы предоставляют разные возможности для анализа, что обусловлено их математической основой.
| Характеристика | Линейные диаграммы | Круговые диаграммы |
|---|---|---|
| Математическая основа | Линейная функция: \(\dot{I} = \dot{I}_1 + k\dot{I}_2\) | Дробно-линейная функция: \(\dot{I} = \frac{A}{B + kC}\) |
| Геометрический годограф | Прямая линия | Окружность (или дуга окружности) |
| Типичный переменный параметр | Коэффициент \(k\) (например, в цепях с источниками) | Физический параметр: \(R, L, C, X_C, X_L, G, B\) |
| Классические области применения | Относительно редки, анализ схем с идеальными источниками. | Анализ RLC-цепей, линии электропередач, диаграмма асинхронного двигателя. |
| Сложность построения | Низкая. | Средняя, требует точных геометрических построений. |
Преимущества круговых диаграмм:
- Наглядность: Позволяют одним взглядом оценить, как меняются модуль и фаза тока при изменении параметра.
- Многопараметричность анализа: С помощью одной диаграммы можно анализировать не только ток \(\dot{I}\), но и активную (\(P\)), реактивную (\(Q\)) и полную (\(S\)) мощности, а также коэффициент мощности \(\cos\phi\).
- Оптимизация: Позволяют легко найти режимы, представляющие практический интерес: максимальный ток (резонанс напряжений), максимальная активная мощность, режим \(\cos\phi = 1\) (резонанс токов).
Недостатки:
- Точность: Как любой графический метод, он ограничен точностью построений и измерений (погрешности циркуля, линейки, транспортира). Уступает современным численным методам.
- Ограниченность: Метод в его классическом виде применим только при изменении одного параметра цепи.
- Трудоемкость: Построение, особенно нахождение центра окружности и ЛПП, требует времени и аккуратности.
Интересные факты о диаграммах в теории цепей
- Связь с диаграммой Смита: Круговая диаграмма является прямым математическим «предком» диаграммы Смита, которая является основным инструментом инженера в области СВЧ. Диаграмма Смита — это, по сути, круговая диаграмма, отображающая комплексный коэффициент отражения.
- Анализ асинхронных двигателей: Одно из важнейших практических применений круговых диаграмм — построение диаграммы Хэя-Оссанны для асинхронного двигателя. Она позволяет по данным опытов холостого хода и короткого замыкания построить годограф вектора тока статора, который (с некоторыми допущениями) является окружностью, и по нему определить все рабочие характеристики двигателя (мощность, КПД, \(\cos\phi\)).
- Инструмент до-компьютерной эры: До появления доступных компьютеров и ПО для моделирования (вроде PSpice или MATLAB), круговые диаграммы были основным рабочим инструментом инженера-электрика для сложных расчетов и оптимизации цепей.
- Математическая элегантность: Вся теория круговых диаграмм базируется на изящном свойстве дробно-линейного преобразования из теории функций комплексного переменного, которое всегда отображает окружности и прямые в окружности или прямые.
- Двойственность мощности: На диаграмме тока (как в Примере 1) можно легко анализировать мощности. Отрезок, пропорциональный \(I \cos\phi\), дает активную мощность \(P\), а отрезок, пропорциональный \(I \sin\phi\), — реактивную \(Q\).
- Возможность двух резонансов: Как показано в Примере 2, в сложных параллельных цепях (третьего и выше порядка) может существовать два разных значения переменного параметра (например, две разные емкости), при которых наступает резонанс токов.
- Графическая инверсия: Годограф импеданса \(Z = Z_1 + kZ_2\) — это прямая линия. Годограф проводимости \(Y = 1/Z\) — это окружность (результат инверсии). А так как \(\dot{I} = \dot{U} \cdot Y\), годограф тока \(\dot{I}\) просто поворачивается и масштабируется по отношению к \(Y\), оставаясь окружностью.
Часто задаваемые вопросы (FAQ)
1. В чем разница между векторной диаграммой и круговой диаграммой?
Векторная диаграмма (или фазорная диаграмма) — это статическое изображение. Она показывает векторы токов и напряжений и их взаимные фазовые сдвиги для одного конкретного режима работы цепи. Круговая диаграмма — это динамическое изображение (годограф). Она показывает, как изменяется один из векторов (например, тока) при плавном изменении одного параметра цепи (R, L или C).
2. Почему годограф — именно окружность, а не эллипс или другая фигура?
Это строгое математическое следствие. Полное сопротивление цепи вида \(Z(k) = Z_1 + kZ_2\) на комплексной плоскости описывает прямую линию. Ток \(\dot{I} = \dot{U} / Z(k)\) является результатом преобразования \(w = 1/z\) (инверсия), примененного к этой прямой. Инверсия прямой, не проходящей через начало координат, всегда дает окружность, проходящую через начало координат.
3. Что такое «линия переменного параметра» (ЛПП)?
ЛПП — это вспомогательная «масштабная линейка», построенная на той же диаграмме. Она позволяет установить прямое соответствие между точкой на окружности (которая представляет ток \(\dot{I}\)) и значением переменного параметра (\(R\), \(X_L\) или \(X_C\)), который вызвал этот ток.
4. Что физически означает вектор \(\dot{I}_k\)?
Это «базисный ток», который служит хордой для построения окружности. Физически он соответствует току в цепи при значении переменного параметра \(k=0\). Например, в Примере 1 (цепь с \(Z_Э — jX_C\)) \(\dot{I}_k\) — это ток при \(X_C = 0\) (т.е. при коротком замыкании конденсатора, \(C=\infty\)). В Примере 2 (цепь с \(R — jX_C\)) \(\dot{I}_k\) — это ток при \(X_C = 0\), то есть ток \(\dot{U}/R\).
5. Можно ли использовать этот метод, если меняются два параметра (например, R и L)?
Нет. Классический метод круговых диаграмм разработан для анализа цепи при изменении только одного действительного параметра. Если одновременно изменять два параметра (например, \(R\) и \(L\)), годограф тока будет не линией (окружностью), а целой областью на комплексной плоскости.
6. Актуальны ли эти методы сегодня, в эру компьютеров?
Для точных численных расчетов — нет, компьютерные симуляторы (PSpice, LTspice, MATLAB) быстрее и точнее. Однако их ценность огромна в образовательном и аналитическом плане. Они дают инженеру «чувство цепи» — качественное понимание того, как система реагирует на изменения, что не всегда очевидно при простом переборе вариантов в симуляторе.
7. Что происходит, если хорда \(\dot{I}_k\) становится диаметром?
Это особый, но частый случай, который сильно упрощает построение. Это происходит, когда угол \(\psi = \pm 90^\circ\). Физически это означает, что постоянная часть импеданса (\(Z_1\)) и переменная часть (\(Z_2\)) являются «ортогональными» — одна чисто активная, а другая — чисто реактивная (как в Примере 2, где \(Z_1 = R\) и \(Z_2 = -j\)).
Заключение
Линейные и, в особенности, круговые диаграммы представляют собой мощный и наглядный графический аппарат для анализа режимов работы цепей синусоидального тока с одним переменным параметром. Они позволяют не только рассчитать, но и визуально представить поведение цепи, что критически важно для понимания таких явлений, как резонанс, передача мощности и фазовые сдвиги.
Несмотря на доминирование компьютерных методов моделирования, круговые диаграммы сохраняют свою значимость как фундаментальный инструмент теории цепей, развивающий инженерную интуицию, а также как теоретическая основа для более сложных методов анализа, например, в СВЧ-технике (диаграмма Смита) или в электроприводе (диаграмма асинхронного двигателя).
Нормативная база и стандартизация
- ГОСТ 2.721-74 Единая система конструкторской документации. Обозначения условные графические в схемах. Обозначения общего применения.
- ГОСТ Р 52002-2003 Электротехника. Термины и определения основных понятий. Определяет фундаментальные понятия, такие как «электрическая цепь», «синусоидальный ток», «активная мощность» и «реактивная мощность».
Список литературы
- Бессонов Л.А. Теоретические основы электротехники (ТОЭ). Электрические цепи. — 11-е изд. — М.: Гардарики, 2007. — 701 с.
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей (ОТЦ). — 5-е изд. — М.: Энергоатомиздат, 1989. — 528 с.
- Атабеков Г.И. Теоретические основы электротехники. Линейные электрические цепи. — 7-е изд. — СПб.: Лань, 2009. — 592 с.
- Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники: в 2 т. — 3-е изд. — Л.: Энергоиздат, 1981. — Т. 1. — 536 с.