Комплексный метод расчета цепей синусоидального тока

Содержание страницы

1. Теоретические основы комплексного метода
2. Анализ пассивных элементов цепи в комплексной форме
3. Последовательная цепь RLC и резонанс напряжений
4. Энергетические соотношения в цепях переменного тока
5. Сравнительная таблица параметров элементов R, L, C
6. Практический пример расчета
7. Преимущества и ограничения комплексного метода
8. Интересные факты о переменном токе
9. FAQ:
Заключение

Расчет электрических цепей переменного тока является фундаментальной задачей электротехники. В отличие от цепей постоянного тока, где все величины стационарны, в цепях синусоидального тока напряжения и токи непрерывно изменяются во времени. Прямой расчет таких цепей через дифференциальные уравнения чрезвычайно трудоемок, особенно для разветвленных схем.

Революционным шагом в развитии теории цепей стало внедрение символического (комплексного) метода. Исторически этот метод связан с именами выдающихся ученых конца XIX — начала XX века: Чарльза Протеуса Штейнмеца и Артура Кеннелли. Именно Штейнмец в 1893 году представил доклад на Международном электрическом конгрессе, где предложил использовать комплексные числа для упрощения анализа цепей переменного тока. Это позволило свести сложные интегро-дифференциальные уравнения к относительно простым алгебраическим, аналогичным закону Ома для постоянного тока.

Примечание: Современная электроэнергетика и радиотехника базируются на синусоидальных токах (или сигналах, которые можно разложить на синусоидальные составляющие через ряд Фурье). Комплексный метод является основным инструментом инженера для расчета установившихся режимов таких цепей, позволяя оперировать не мгновенными значениями, а их интегральными характеристиками — векторами (фазорами) на комплексной плоскости.

1. Теоретические основы комплексного метода

Сущность комплексного метода заключается в переходе от оригиналов — синусоидальных функций времени $ i(t), u(t), e(t) $ — к их изображениям в виде комплексных чисел. Это преобразование основано на формуле Эйлера: $ e^{j\alpha} = \cos\alpha + j\sin\alpha $.

Режим работы цепи описывается системой дифференциальных уравнений. Поскольку производная и интеграл от синусоидальной функции также являются синусоидальными функциями той же частоты, им можно поставить в соответствие комплексные числа. В электротехнике мнимая единица обозначается буквой $ j $ (чтобы не путать с током $ i $), где $ j^2 = -1 $.

1.1. Преобразование производных и интегралов

Для синусоидального тока $ i(t) $ его комплексное изображение (комплексная амплитуда) обозначается $\dot{I}_m$. Тогда операции дифференцирования и интегрирования во временной области заменяются алгебраическими операциями в комплексной области:

Мгновенное значение: $ i(t) \rightarrow \dot{I}_m e^{j\omega t} $
Производная: $ \frac{di(t)}{dt} \rightarrow j\omega \dot{I}_m e^{j\omega t} $
Интеграл: $ \int i(t)dt \rightarrow \frac{1}{j\omega} \dot{I}_m e^{j\omega t} $

В общем виде для производной n-го порядка:

$$ \frac{d^n i(t)}{dt^n} \rightarrow (j\omega)^n \dot{I}_m e^{j\omega t} $$

где $ \omega $ — угловая частота, измеряемая в рад/с.

Такая замена позволяет перейти от дифференциальных уравнений к алгебраическим, оперируя комплексными токами, напряжениями и электродвижущими силами (ЭДС).

2. Анализ пассивных элементов цепи в комплексной форме

Рассмотрим поведение базовых идеализированных элементов — резистора, индуктивности и конденсатора — при воздействии синусоидального тока $ i = I_m \sin\omega t $.

2.1. Активное сопротивление (Резистор R)

На резисторе напряжение и ток совпадают по фазе. Мгновенное значение напряжения определяется законом Ома: $ u = iR = R I_m \sin\omega t = U_m \sin\omega t $.

Фазовый сдвиг $ \varphi = \varphi_u — \varphi_i = 0 $.

Мгновенная мощность (см. Рис. 1а) пульсирует с двойной частотой относительно среднего значения:

$$ p = ui = U_m I_m \sin^2\omega t = \frac{U_m I_m}{2}(1 — \cos 2\omega t) $$

Постоянная составляющая этой мощности называется активной мощностью $ P $ и характеризует необратимое преобразование электрической энергии в другие виды (например, тепловую):

$$ P = \frac{U_m I_m}{2} = UI \quad [Вт] $$

где $ U $ и $ I $ — действующие значения напряжения и тока.

(а) — Графики мгновенных значений тока i(t), напряжения u(t) и мощности p(t). Ток и напряжение синфазны, мощность всегда положительна.
(б) — Векторная диаграмма на комплексной плоскости: векторы тока и напряжения совпадают по направлению.

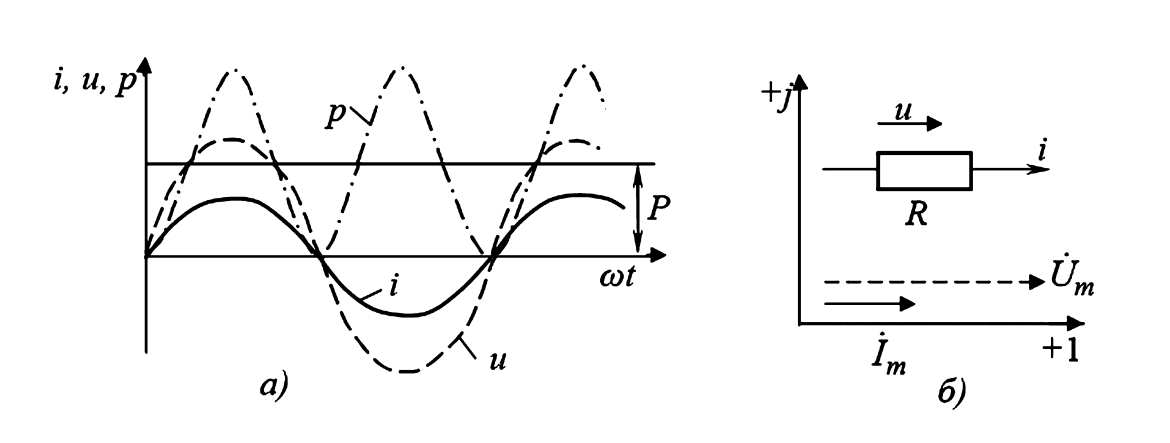
Рисунок 1 — Характеристики цепи с резистором R

2.2. Индуктивность (Катушка L)

В идеальной индуктивности протекание переменного тока вызывает возникновение ЭДС самоиндукции. Напряжение на зажимах индуктивности определяется скоростью изменения тока:

$$ u_L = L\frac{di}{dt} = L\frac{d(I_m \sin\omega t)}{dt} = \omega L I_m \cos\omega t = U_{Lm} \sin(\omega t + 90^\circ) $$

Напряжение на индуктивности опережает ток на угол $ 90^\circ $ ($ \pi/2 $). Величина $ X_L = \omega L $ называется индуктивным сопротивлением (измеряется в Омах).

В комплексной форме опережение на $ 90^\circ $ соответствует умножению на $ j $:

$$ \dot{U}_{Lm} = j X_L \dot{I}_{Lm} = j\omega L \dot{I}_m $$

Мгновенная мощность индуктивности колеблется симметрично относительно нуля, не совершая полезной работы (среднее значение за период равно 0). Индуктивность циклически запасает энергию в магнитном поле и возвращает её обратно в источник.

(а) — Графики: напряжение u(t) достигает максимума раньше тока i(t) на четверть периода.
(б) — Векторная диаграмма: вектор напряжения повернут на 90 градусов против часовой стрелки относительно вектора тока.

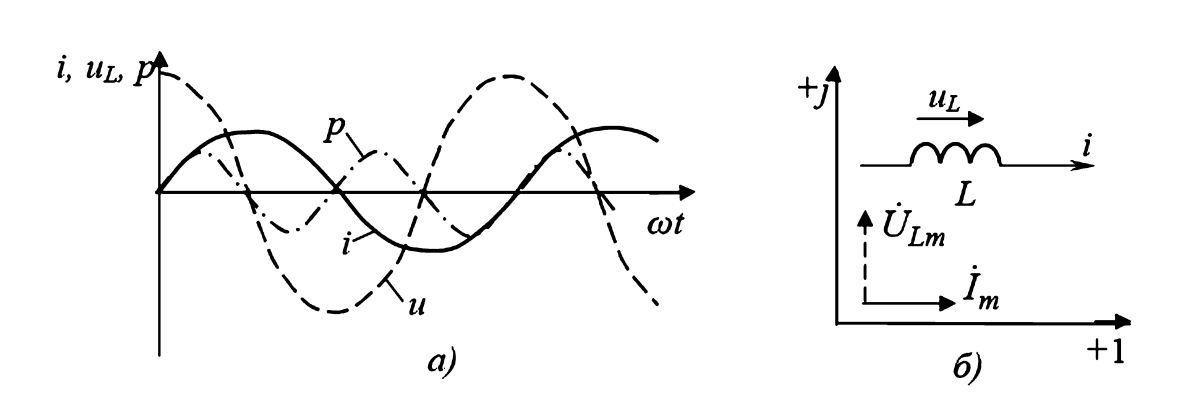
Рисунок 2 — Характеристики цепи с индуктивностью L

2.3. Емкость (Конденсатор C)

Ток через конденсатор пропорционален скорости изменения напряжения на нем, следовательно, напряжение интегрально зависит от тока:

$$ u_C = \frac{1}{C} \int i dt = \frac{1}{C} \int I_m \sin\omega t dt = -\frac{I_m}{\omega C} \cos\omega t = U_{Cm} \sin(\omega t — 90^\circ) $$

Напряжение на емкости отстает от тока на угол $ 90^\circ $ ($ \pi/2 $). Величина $ X_C = \frac{1}{\omega C} $ называется емкостным сопротивлением (Ом).

В комплексной форме отставание на $ 90^\circ $ соответствует умножению на $ -j $ (или делению на $ j $):

$$ \dot{U}_{Cm} = -j X_C \dot{I}_m = \frac{1}{j\omega C} \dot{I}_m $$

Емкость, как и индуктивность, не потребляет активной мощности, циклически запасая энергию в электрическом поле.

(а) — Графики: напряжение u(t) достигает максимума позже тока i(t) на четверть периода.
(б) — Векторная диаграмма: вектор напряжения повернут на 90 градусов по часовой стрелке относительно вектора тока.

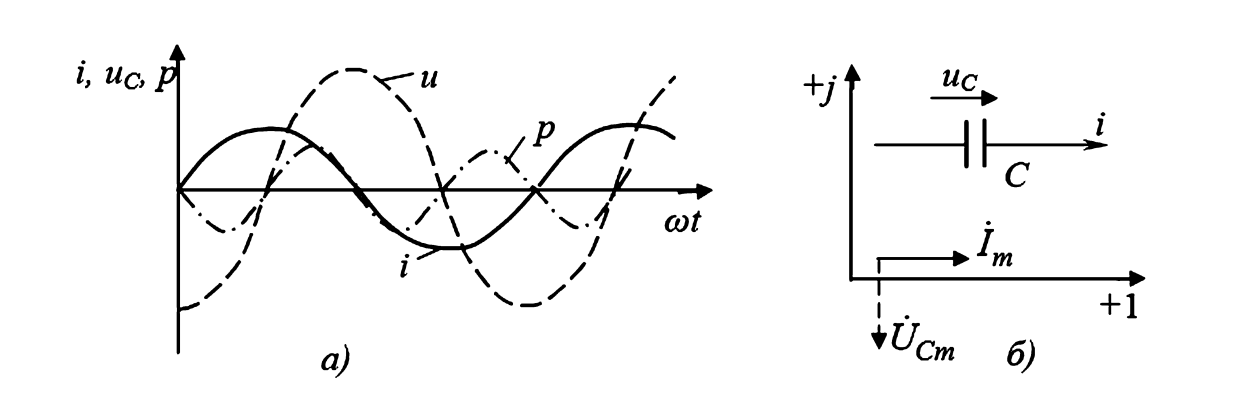
Рисунок 3 — Характеристики цепи с конденсатором C

3. Последовательная цепь RLC и резонанс напряжений

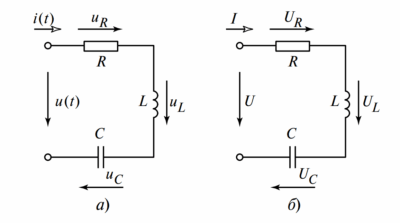
Рассмотрим классическую цепь, где резистор R, индуктивность L и емкость C включены последовательно к источнику синусоидального напряжения. Согласно второму закону Кирхгофа для мгновенных значений:

$$ u = u_R + u_L + u_C = iR + L\frac{di}{dt} + \frac{1}{C}\int i dt $$

Используя комплексный метод, это интегро-дифференциальное уравнение преобразуется в простое алгебраическое уравнение для комплексных амплитуд (или действующих значений):

$$ \dot{U} = \dot{U}_R + \dot{U}_L + \dot{U}_C = R\dot{I} + j\omega L\dot{I} — j\frac{1}{\omega C}\dot{I} = \left[ R + j\left(\omega L — \frac{1}{\omega C}\right) \right] \dot{I} $$

Выражение в квадратных скобках называется комплексным сопротивлением (импедансом) цепи $ \underline{Z} $:

$$ \underline{Z} = R + j(X_L — X_C) = R + jX = Ze^{j\varphi} $$

где $ X = X_L — X_C $ — реактивное сопротивление цепи.

Модуль полного сопротивления:

$$ Z = \sqrt{R^2 + X^2} = \sqrt{R^2 + (\omega L — \frac{1}{\omega C})^2} $$

Угол сдвига фаз между напряжением и током определяется как $ \varphi = \text{arctg}\frac{X}{R} $.

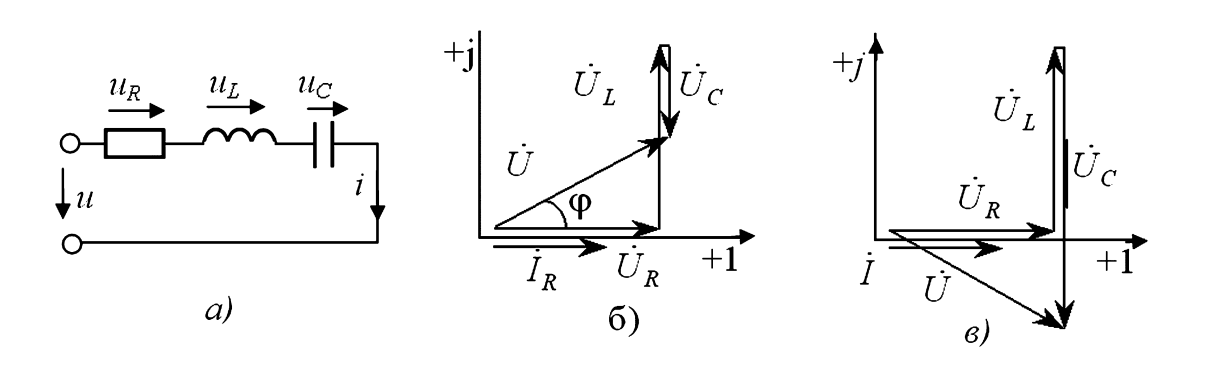
(а) — Принципиальная схема: R, L, C соединены последовательно.
(б) — Векторная диаграмма при индуктивном характере (XL > XC): общий ток отстает от напряжения источника.
(в) — Векторная диаграмма при емкостном характере (XL < XC): общий ток опережает напряжение источника.
Рисунок 4 — Векторные диаграммы последовательной цепи RLC

Важно: В последовательной цепи возможно явление, когда $ X_L = X_C $. При этом реактивное сопротивление цепи становится равным нулю, а ток достигает максимума, ограничиваясь только активным сопротивлением R. Это явление называется резонансом напряжений. При резонансе напряжения на реактивных элементах могут многократно превышать напряжение источника, что опасно для изоляции электроустановок.

4. Энергетические соотношения в цепях переменного тока

В цепях синусоидального тока, помимо мгновенной мощности, оперируют интегральными понятиями мощности.

4.1. Виды мощности

Активная мощность (P) — средняя за период мощность, характеризующая необратимое потребление энергии. Измеряется в ваттах [Вт].
$$ P = UI \cos\varphi = I^2 R $$
Реактивная мощность (Q) — характеризует энергию, циркулирующую между источником и реактивными элементами цепи. Не совершает полезной работы, но нагружает линии передачи. Измеряется в вольт-амперах реактивных [вар].
$$ Q = UI \sin\varphi = I^2 (X_L — X_C) = Q_L — Q_C $$
Полная мощность (S) — произведение действующих значений тока и напряжения. Характеризует предельную нагрузочную способность оборудования. Измеряется в вольт-амперах [В·А].
$$ S = UI = \sqrt{P^2 + Q^2} $$

4.2. Комплексная мощность и треугольник мощностей

Удобным инструментом является понятие комплексной мощности $\tilde{S}$, которая определяется как произведение вектора напряжения на сопряженный вектор тока:

$$ \tilde{S} = \dot{U} \dot{I}^* = (Ue^{j\varphi_u})(Ie^{-j\varphi_i}) = UIe^{j(\varphi_u — \varphi_i)} = UIe^{j\varphi} = P + jQ $$

Графически взаимосвязь мощностей представляется в виде треугольника мощностей.

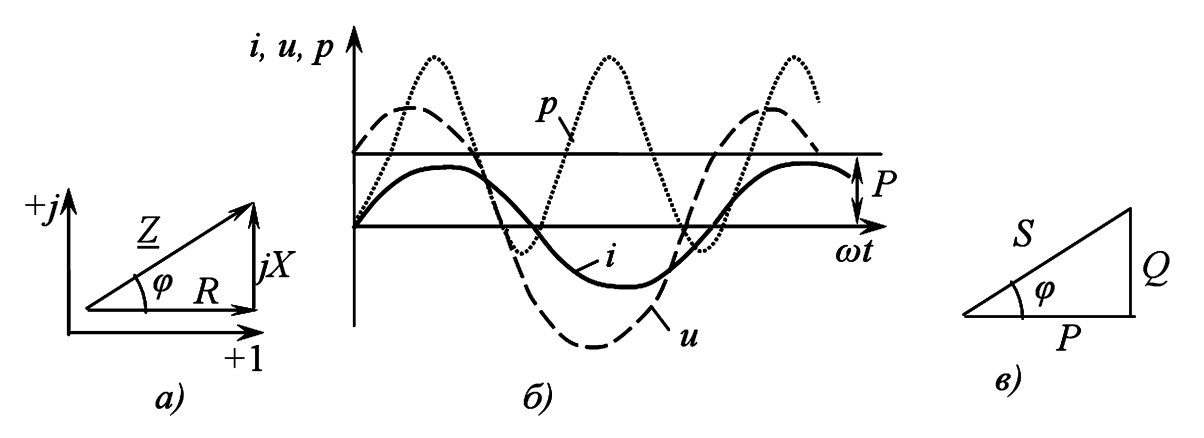
Треугольники сопротивлений и мощностей:

(а) — Треугольник сопротивлений: катеты R и X, гипотенуза Z.
(б) — Мгновенная мощность в цепи RLC: пульсации с двойной частотой относительно уровня P.
(в) — Треугольник мощностей: катеты P (активная) и Q (реактивная), гипотенуза S (полная).
Рисунок 5 — Графическое представление параметров цепи

Коэффициент мощности $ \cos\varphi = P/S $ — важнейший технико-экономический показатель. Низкий $ \cos\varphi $ означает неэффективное использование электроэнергии и повышенные потери в сетях.

5. Сравнительная таблица параметров элементов R, L, C

Параметр	Резистор (R)	Индуктивность (L)	Емкость (C)
Связь u и i (мгновен.)	$ u = iR $	$ u = L \frac{di}{dt} $	$ u = \frac{1}{C} \int i dt $
Комплексное сопротивление	$ Z_R = R $	$ Z_L = j\omega L $	$ Z_C = -j\frac{1}{\omega C} = \frac{1}{j\omega C} $
Фазовый сдвиг ($\varphi_u — \varphi_i$)	0 (в фазе)	+90° (напряжение опережает)	-90° (напряжение отстает)
Потребление энергии	Активная (P > 0, Q = 0)	Реактивная индуктивная (P = 0, Q > 0)	Реактивная емкостная (P = 0, Q < 0)
Зависимость от частоты	Не зависит (в идеале)	Растет пропорционально $\omega$	Падает обратно пропорционально $\omega$

6. Практический пример расчета

Задача: Катушка индуктивности и конденсатор включены последовательно в сеть с напряжением 220 В промышленной частоты (50 Гц). Активное сопротивление катушки $ R_k = 10 $ Ом, ее индуктивность $ L_k = 0,1 $ Гн. Емкость конденсатора $ C = 50 $ мкФ. Необходимо определить токи и напряжения на элементах.

(а) — Схема: источник U, последовательно Rk, Lk, C.
(б, в) — Векторные диаграммы для разных начальных фаз.

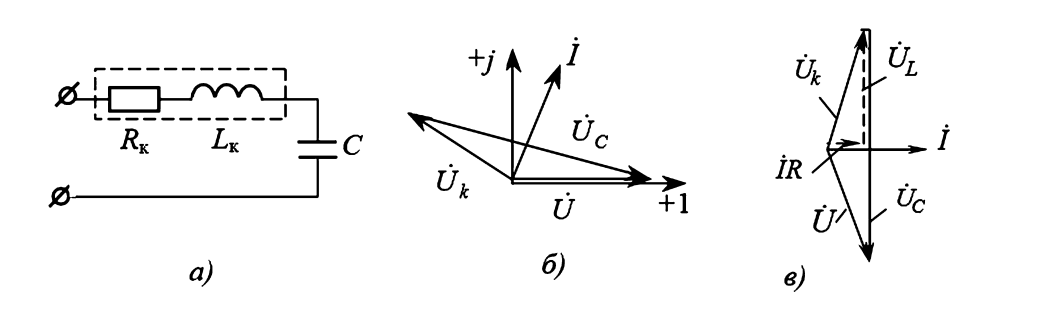
Рисунок 6 — Иллюстрации к примеру расчета

Решение

Шаг 1. Определение параметров цепи.

Угловая частота: $ \omega = 2\pi f = 2 \cdot 3,14 \cdot 50 = 314 $ рад/с.

Индуктивное сопротивление: $ X_L = \omega L_k = 314 \cdot 0,1 = 31,4 $ Ом.

Емкостное сопротивление: $ X_C = \frac{1}{\omega C} = \frac{1}{314 \cdot 50 \cdot 10^{-6}} \approx 63,7 $ Ом.

Шаг 2. Расчет комплексного сопротивления.

$$ \underline{Z} = R_k + j(X_L — X_C) = 10 + j(31,4 — 63,7) = 10 — j32,3 \text{ Ом} $$

В показательной форме:

$$ \underline{Z} = \sqrt{10^2 + (-32,3)^2} \cdot e^{j \cdot \text{arctg}(-32,3/10)} \approx 33,8 \cdot e^{-j72,8^\circ} \text{ Ом} $$

Цепь имеет емкостный характер, так как $ X_C > X_L $.

Шаг 3. Расчет тока.

Примем начальную фазу напряжения равной нулю: $ \dot{U} = 220 e^{j0^\circ} $ В.

$$ \dot{I} = \frac{\dot{U}}{\underline{Z}} = \frac{220 e^{j0^\circ}}{33,8 e^{-j72,8^\circ}} \approx 6,5 e^{j72,8^\circ} \text{ А} $$

Действующее значение тока — 6,5 А. Ток опережает напряжение на 72,8°.

Шаг 4. Расчет напряжений на элементах.

На конденсаторе: $ \dot{U}_C = \dot{I} (-jX_C) = 6,5 e^{j72,8^\circ} \cdot 63,7 e^{-j90^\circ} \approx 414 e^{-j17,2^\circ} $ В.
На катушке (учитывая её активное сопротивление):
$$ \underline{Z}_k = R_k + jX_L = 10 + j31,4 \approx 33 e^{j72,3^\circ} \text{ Ом} $$
$$ \dot{U}_k = \dot{I} \cdot \underline{Z}_k = 6,5 e^{j72,8^\circ} \cdot 33 e^{j72,3^\circ} \approx 214,5 e^{j145,1^\circ} \text{ В} $$

Интересное наблюдение: Напряжение на конденсаторе (414 В) значительно превышает напряжение источника (220 В). Это типичный эффект в цепях, близких к резонансу.

7. Преимущества и ограничения комплексного метода

Преимущества:

Снижение сложности: Замена интегро-дифференциальных уравнений алгебраическими существенно упрощает математические выкладки.
Универсальность: Позволяет использовать все методы расчета цепей постоянного тока (метод контурных токов, узловых потенциалов, эквивалентного генератора) для цепей переменного тока.
Наглядность: Возможность построения векторных диаграмм для качественного анализа режимов работы.

Ограничения:

Только установившийся режим: Метод применим только для расчета установившихся режимов. Для анализа переходных процессов требуются другие методы (например, операторный метод с преобразованием Лапласа).
Линейность: Метод корректно работает только в линейных цепях. При наличии нелинейных элементов (диоды, насыщающиеся дроссели) форма тока перестает быть синусоидальной.

8. Интересные факты о переменном токе

Война токов: Внедрение переменного тока сопровождалось жесткой конкуренцией между Томасом Эдисоном (постоянный ток) и Николой Теслой с Джорджем Вестингаузом (переменный ток). Победа переменного тока обусловлена простотой трансформации напряжения.
Стандарт 50/60 Гц: Выбор частоты был компромиссом. Слишком низкая частота вызывает заметное мерцание ламп, слишком высокая — увеличивает потери в индуктивностях линий передач и усложняет конструкцию генераторов.
Скин-эффект: На высоких частотах переменный ток вытесняется к поверхности проводника, из-за чего эффективное сечение уменьшается, а активное сопротивление растет.
Резонансные катастрофы: Неучтенный резонанс в промышленных сетях может приводить к разрушению конденсаторных батарей и измерительных трансформаторов из-за перенапряжений.
Мнимая единица: Инженеры используют $ j $ вместо математического $ i $, потому что $ i $ в электротехнике традиционно занято для мгновенного значения тока.
Косинус «фи»: Энергокомпании штрафуют крупных потребителей за низкий коэффициент мощности, так как это заставляет их гонять по сетям «бесполезный» реактивный ток.
Идеальных элементов нет: Реальный конденсатор имеет утечку (параллельное R) и индуктивность выводов (последовательная L), что важно учитывать на высоких частотах.

9. FAQ:

1. Почему комплексный метод работает только для синусоиды?

Потому что только экспоненциальная функция $ e^{st} $ (где s — комплексная частота) при дифференцировании сохраняет свою форму, меняя лишь множитель. Синусоида — это комбинация комплексных экспонент (по формуле Эйлера).

2. Что физически означает мнимая часть комплексной мощности?

Мнимая мощность (реактивная, Q) — это скорость обмена энергией между генератором и магнитными/электрическими полями цепи. Она не греет провода (напрямую), но нагружает их током.

3. Можно ли измерить комплексное сопротивление мультиметром?

Обычным — нет. Требуется специальный прибор — RLC-метр (импедансметр), который подает тестовый сигнал переменного тока и измеряет не только амплитуды, но и фазовый сдвиг.

4. Что такое «векторная диаграмма» простыми словами?

Это «фотография» вращающихся векторов напряжений и токов, сделанная в определенный момент времени. Она помогает визуально оценить, что опережает, что отстает и как складываются напряжения.

5. Где применяется этот метод кроме энергетики 50 Гц?

Везде, где есть аналоговые сигналы: в аудиотехнике (расчет фильтров и кроссоверов), в радиотехнике, в системах связи и автоматического управления.

6. Почему напряжение на конденсаторе может быть больше напряжения сети?

В последовательном контуре при резонансе энергия «раскачивается» между L и C. ЭДС самоиндукции катушки складывается с напряжением сети в нужной фазе, «накачивая» конденсатор до высоких напряжений.

7. В чем отличие активного сопротивления от импеданса?

Активное сопротивление (R) — это только вещественная часть импеданса. Импеданс (Z) — это полное комплексное сопротивление, учитывающее и потери энергии (R), и фазовые сдвиги (X).

Заключение

Комплексный метод расчета является краеугольным камнем теоретической электротехники. Позволяя абстрагироваться от временной зависимости и перейти к геометрическому и алгебраическому представлению процессов, он превратил искусство интуитивного понимания электрических явлений в строгую инженерную дисциплину.

Освоение этого метода необходимо любому специалисту, работающему с электроникой, энергетикой или автоматикой, так как это язык, на котором «разговаривают» современные электрические цепи.

Нормативная база и литература

При выполнении расчетов и оформлении технической документации необходимо руководствоваться следующими актуальными стандартами (действующими на территории РФ и стран ЕАЭС):

ГОСТ Р 52002-2003 Электротехника. Термины и определения основных понятий.
ГОСТ IEC 60050-131-2015 Международный электротехнический словарь. Часть 131. Теория электрических цепей.
ГОСТ 2.701-2008 Единая система конструкторской документации (ЕСКД). Схемы. Виды и типы. Общие требования к выполнению.
ГОСТ 8.417-2002 Государственная система обеспечения единства измерений (ГСИ). Единицы величин.

Рекомендуемая литература: Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2023.