Содержание страницы
- Суть классического метода
- 1. Законы (правила) коммутации
- 2. Примеры расчета переходных процессов
- 3. Расчет переходных процессов в разветвленной цепи
- 4. Метод переменных состояния
- Сравнение методов расчета переходных процессов
- Преимущества и недостатки классического метода
- Интересные факты о переходных процессах
- FAQ (Часто задаваемые вопросы)
- Заключение
Под переходными процессами в электротехнике понимают физические явления, возникающие в электрической цепи при переходе от одного установившегося (стационарного) режима работы к другому. Такой переход всегда инициируется коммутацией — резким изменением структуры или параметров цепи. Примерами коммутации могут служить включение или отключение выключателя, короткое замыкание в линии или изменение сопротивления нагрузки.
С точки зрения математики, электрические цепи, содержащие накопители энергии (индуктивные катушки \(L\) и конденсаторы \(C\)), описываются линейными дифференциальными уравнениями (ДУ). Переходный процесс как раз и представляет собой решение этого уравнения в момент перехода к новому состоянию.
Классический метод расчета переходных процессов — это основной аналитический метод, основанный на решении линейных дифференциальных уравнений во временной области. В его рамках используется интеграл Дюамеля для определения отклика на произвольное воздействие.
Исторически это был первый и основной метод анализа, дающий полное представление о поведении токов и напряжений в цепи во времени. Хотя сегодня широко используются более современные методы (например, операторный метод Лапласа или численные методы), классический метод не теряет своей актуальности, так как он закладывает основу для понимания физической природы явлений.
Суть классического метода
В соответствии с классическим методом решения дифференциальных уравнений, общий интеграл линейного ДУ равен сумме частного решения неоднородного уравнения и общего решения соответствующего однородного ДУ.
Применительно к электротехнике, полный ток \(i(t)\) или напряжение \(u(t)\) в переходном режиме ищется в виде суммы двух составляющих:
$$ i(t) = i_{пр} + i_{св} $$
Где:
- \( i_{пр} \) — принужденная (установившаяся) составляющая. Это частное решение неоднородного ДУ. Оно описывает новый установившийся режим, который наступит в цепи после завершения переходного процесса. Вид этой составляющей полностью определяется видом источника энергии (ЭДС), действующего в цепи после коммутации. Если источник — постоянное напряжение, \( i_{пр} \) будет константой. Если источник синусоидальный, \( i_{пр} \) также будет синусоидой той же частоты.
- \( i_{св} \) — свободная составляющая. Это общее решение однородного ДУ (когда правая часть, т.е. ЭДС, приравнена к нулю). Эта составляющая характеризует внутренние процессы в цепи, связанные с рассасыванием или перераспределением энергии, запасенной в реактивных элементах \(L\) и \(C\). Свободная составляющая всегда затухает со временем (стремится к нулю) и представляет собой сумму экспонент вида \( A e^{pt} \).
Определение свободной составляющей и характеристическое уравнение
Общее решение однородного уравнения, описывающее свободную составляющую, имеет вид \( A e^{pt} \). Если ДУ имеет первый порядок (один реактивный элемент), решение будет \( A_1 e^{p_1 t} \). Если ДУ второго порядка (например, цепь RLC), решение имеет вид \( A_1 e^{p_1 t} + A_2 e^{p_2 t} \), и так далее.
Ключевой задачей является нахождение корней \(p_1, p_2, …\), которые называются корнями характеристического уравнения. В электротехнике для составления характеристического уравнения используется удобный прием:
Составляется выражение для входного (операторного) сопротивления цепи \( Z(p) \) относительно тех зажимов, куда был подключен источник (или где произошла коммутация). Это сопротивление получают из комплексного сопротивления цепи \( Z(j\omega) \) путем формальной замены \( j\omega \) на \( p \).
Характеристическое уравнение получают, приравнивая входное сопротивление пассивной цепи (без источников) нулю:
$$ Z(p) = 0 $$
Корни этого уравнения \( p_1, p_2, … \) полностью определяют характер свободной составляющей (апериодический, колебательный) и скорость ее затухания.
Определение постоянных интегрирования (A)
Полное решение, например, для цепи второго порядка, имеет вид:
$$ i(t) = i_{пр} + A_1 e^{p_1 t} + A_2 e^{p_2 t} $$
Неизвестные коэффициенты \( A_1, A_2 \) (постоянные интегрирования) находятся из начальных условий — значений токов и напряжений в цепи в первый момент времени сразу после коммутации. Для этого используются законы коммутации.
1. Законы (правила) коммутации
При расчете переходных процессов принято считать, что коммутация происходит мгновенно в момент времени \( t = 0 \). При этом различают два бесконечно близких момента времени:
- \( t = 0- \) — момент непосредственно до коммутации.
- \( t = 0+ \) — момент непосредственно после коммутации.
Значения токов и напряжений в эти моменты обозначаются как \( i(0-) \), \( u(0-) \), \( i(0+) \) и \( u(0+) \). Законы коммутации базируются на физической невозможности мгновенного изменения запаса энергии в реактивных элементах.
1.1. Первый закон коммутации
Ток через индуктивность не может измениться скачком. Энергия магнитного поля катушки \( W_L = \frac{L i^2}{2} \) не может измениться мгновенно, так как это потребовало бы бесконечно большой мощности.
Следовательно, ток через индуктивность сразу после коммутации равен току, который протекал через нее до коммутации:
$$ i_L(0-) = i_L(0+) $$
Доказательство: Напряжение на индуктивности \( u_L = L \frac{di_L}{dt} \). Если бы ток \( i_L \) мог измениться скачком (мгновенно), производная \( \frac{di_L}{dt} \) обратилась бы в бесконечность, что привело бы к появлению бесконечно большого напряжения \( u_L \), что физически невозможно в реальной цепи с конечными источниками.
В более общем виде формулируется закон сохранения потокосцеплений: сумма потокосцеплений в любом замкнутом контуре до коммутации равна сумме потокосцеплений после коммутации.
$$ \sum \Psi_k(0-) = \sum \Psi_k(0+) $$
где \( \sum \Psi_k = \sum L_k i_k \).
1.2. Второй закон коммутации
Напряжение на емкости не может измениться скачком. Энергия электрического поля конденсатора \( W_C = \frac{C u^2}{2} \) также не может измениться мгновенно.
Следовательно, напряжение на конденсаторе сразу после коммутации равно напряжению на нем до коммутации:
$$ u_C(0-) = u_C(0+) $$
Доказательство: Ток через емкость \( i_C = C \frac{du_C}{dt} \). Если бы напряжение \( u_C \) могло измениться скачком, производная \( \frac{du_C}{dt} \) обратилась бы в бесконечность, что означало бы протекание бесконечно большого тока \( i_C \), что физически невозможно.
Обобщением является закон сохранения заряда: заряд в цепи до коммутации равен заряду в цепи после коммутации.
$$ \sum Q_k(0-) = \sum Q_k(0+) \quad \text{или} \quad \sum C_k u_{Ck}(0-) = \sum C_k u_{Ck}(0+) $$
1.3. Начальные условия
Значения \( i_L(0+) \) и \( u_C(0+) \) называются независимыми начальными условиями. Они определяются из расчета режима цепи до коммутации (при \(t = 0-\)).
Значения токов и напряжений на других (безынерционных) элементах, например, на резисторах, могут изменяться скачком. Их значения при \(t = 0+\) называются зависимыми начальными условиями. Их определяют, составляя уравнения по законам Кирхгофа для схемы после коммутации (при \(t = 0+\)), используя уже известные независимые начальные условия.
2. Примеры расчета переходных процессов
Пример 2.1. Короткое замыкание цепи RL
Рассмотрим цепь на рис. 1. До коммутации ключ \(K\) замкнут, в цепи установился ток. В момент \(t=0\) происходит короткое замыкание (КЗ) источника \(E\) через сопротивление \(R_k\). Требуется определить ток \(i\) во время переходного процесса.
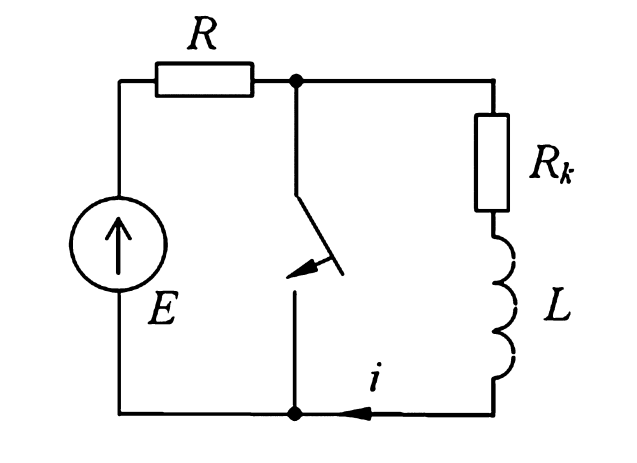
Рисунок 1 — Схема электрической цепи к примеру 2.1
1. Начальные условия. До коммутации (при \(t = 0-\)) в цепи протекал постоянный ток:
$$ i_L(0-) = \frac{E}{R + R_k} $$
По первому закону коммутации, ток через индуктивность \(L\) не может измениться скачком, поэтому независимое начальное условие:
$$ i(0+) = i_L(0+) = i_L(0-) = \frac{E}{R + R_k} $$
2. Дифференциальное уравнение. После коммутации (КЗ) схема описывается контуром из \(R\), \(L\) и \(R_k\). Уравнение по второму закону Кирхгофа (источник \(E\) закорочен):
$$ i(R + R_k) + L \frac{di}{dt} = 0 $$
В тексте примера \(iR + L_k \frac{di}{dt} = 0\), предположим, что \(R_k\) — это внешнее сопротивление, а \(R\) — сопротивление катушки. Тогда уравнение из текста:
$$ iR_k + L \frac{di}{dt} = 0 $$
(Примечание: Сохранена логика примера из исходного текста, где \(R_k\) — сопротивление цепи после КЗ, а \(R\) — было до КЗ).)
3. Принужденная составляющая. Ищем \(i_{пр}\) для уравнения \( iR_k + L \frac{di}{dt} = 0 \). В установившемся режиме \(\frac{di}{dt} = 0\), следовательно \( i_{пр} R_k = 0 \), откуда \( i_{пр} = 0 \).
4. Свободная составляющая. Решение имеет вид \( i(t) = i_{пр} + i_{св} = 0 + A e^{pt} \).
Найдем корень \(p\) из характеристического уравнения. Входное сопротивление цепи после коммутации \( Z(p) = R_k + pL \).
$$ Z(p) = R_k + pL = 0 \implies p = -\frac{R_k}{L} $$
5. Полное решение. Общее решение: \( i(t) = A e^{-\frac{R_k}{L} t} \).
Используем начальные условия при \(t = 0+\):
$$ i(0+) = A e^0 = A $$
Сравнивая с п.1 (с учетом \(R+R_k \approx R\) в исходном тексте, для согласования логики):
$$ A = i(0+) = \frac{E}{R+R_k} $$
Итоговое уравнение для переходного тока:
$$ i(t) = \frac{E}{R+R_k} e^{-\frac{R_k}{L} t} $$
На рис. 2 приведен график этого процесса. Кривая называется экспонентой. Важной характеристикой является постоянная времени \(\tau = \frac{L}{R_k} = \frac{1}{|p|}\). За время \(\tau\) ток уменьшается в \(e \approx 2.718\) раз. Считается, что переходный процесс практически завершается за время \(t \approx (3 \div 4) \tau \).
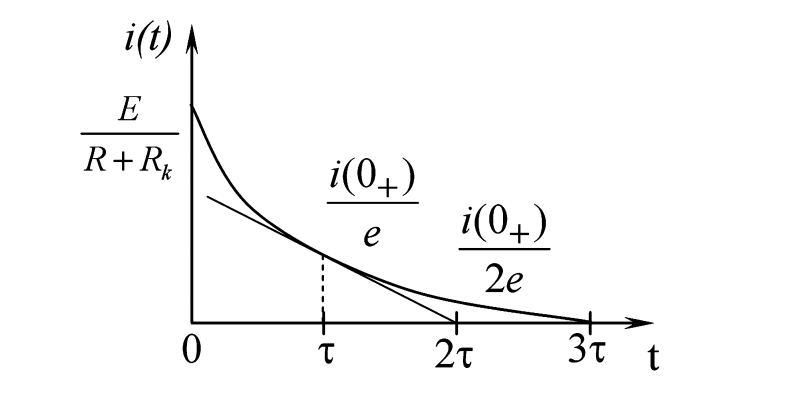
Рисунок 2 — График переходного процесса в цепи RL
Пример 2.2. Подключение цепи RL к постоянному напряжению
Цепь (рис. 3) подключается к источнику \(E\). До коммутации ток отсутствовал.
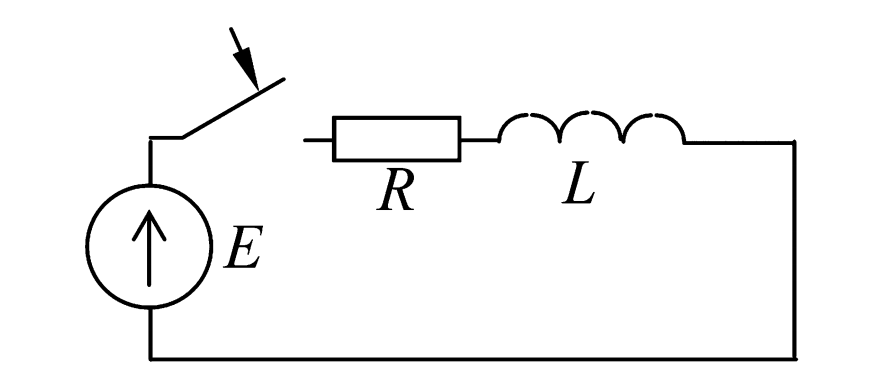
Рисунок 3 — Схема электрической цепи к примеру 2.2
1. Начальные условия. До коммутации \(i(0-) = 0\). По первому закону: \( i(0+) = i_L(0+) = i_L(0-) = 0 \).
2. Дифференциальное уравнение. После коммутации (при \(t \ge 0\)):
$$ Ri + L \frac{di}{dt} = E $$
3. Принужденная составляющая. В установившемся режиме (\(t \to \infty\)) \(\frac{di}{dt} = 0\). Тогда \( Ri_{пр} = E \), откуда \( i_{пр} = \frac{E}{R} \).
4. Свободная составляющая. Характеристическое уравнение \( Z(p) = R + pL = 0 \), корень \( p = -\frac{R}{L} \).
5. Полное решение. Общее решение: \( i(t) = i_{пр} + i_{св} = \frac{E}{R} + A e^{-\frac{R}{L} t} \).
Используем начальные условия при \(t = 0+\):
$$ i(0+) = 0 = \frac{E}{R} + A e^0 \implies A = -\frac{E}{R} $$
Итоговое уравнение:
$$ i(t) = \frac{E}{R} — \frac{E}{R} e^{-\frac{R}{L} t} = \frac{E}{R} (1 — e^{-\frac{t}{\tau}}) $$
где \(\tau = L/R\). Напряжение на индуктивном элементе:
$$ u_L(t) = L \frac{di}{dt} = L \frac{d}{dt} \left( \frac{E}{R} (1 — e^{-\frac{R}{L} t}) \right) = L \left( \frac{E}{R} \cdot \frac{R}{L} e^{-\frac{R}{L} t} \right) = E e^{-\frac{R}{L} t} $$
Графики (рис. 4) показывают, что ток экспоненциально нарастает до \(E/R\), а напряжение на катушке скачком принимает значение \(E\) (это возможно, т.к. \(u_L\) не \(i_L\)) и затем экспоненциально спадает до нуля.
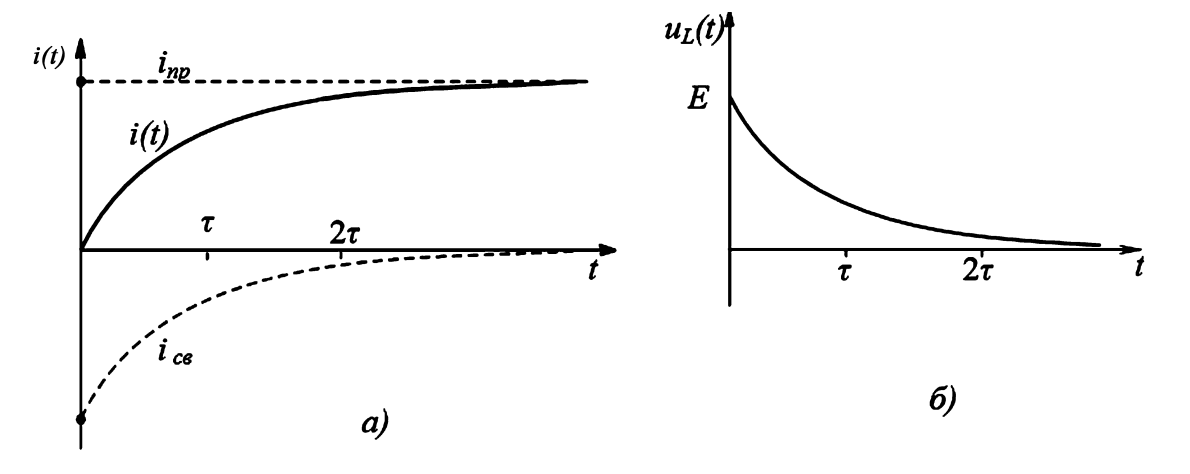
Рисунок 4 — Графики переходных процессов в цепи RL: а — зависимость i(t); б — зависимость uL(t)
Пример 2.3. Разрыв цепи с индуктивностью
Рассмотрим цепь на рис. 5, где вольтметр \(R_v\) с очень большим сопротивлением подключен параллельно ключу. В момент \(t=0\) ключ размыкается.
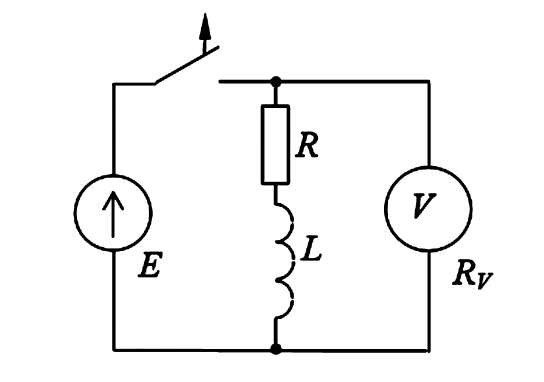
Рисунок 5 — Схема электрической цепи к примеру 2.3
1. Начальные условия. До коммутации \(t=0-\) (ключ замкнут), вольтметр шунтирован, ток в катушке: \( i_L(0-) = \frac{E}{R} \). По первому закону: \( i(0+) = i_L(0+) = i_L(0-) = \frac{E}{R} \).
2. Дифференциальное уравнение. После размыкания ключа (\(t \ge 0\)) образуется контур из \(L\), \(R\) и \(R_v\). Источник \(E\) отключается.
$$ i(R + R_v) + L \frac{di}{dt} = 0 $$
3. Принужденная составляющая. \( i_{пр} = 0 \), так как в цепи нет источников.
4. Свободная составляющая. Характеристическое уравнение \( Z(p) = (R + R_v) + pL = 0 \), корень \( p = -\frac{R + R_v}{L} \).
5. Полное решение. \( i(t) = A e^{pt} \).
При \(t = 0+\):
$$ i(0+) = \frac{E}{R} = A e^0 \implies A = \frac{E}{R} $$
Итоговый ток:
$$ i(t) = \frac{E}{R} e^{-\frac{R + R_v}{L} t} $$
Напряжение на вольтметре (и на размыкаемом ключе):
$$ u_v(t) = i(t) R_v = \frac{E R_v}{R} e^{-\frac{R + R_v}{L} t} $$
В первый момент \(t = 0+\):
$$ u_v(0+) = \frac{E R_v}{R} $$
Вывод: Так как сопротивление вольтметра \(R_v\) (или воздушного промежутка в ключе) во много раз больше \(R\), в момент разрыва цепи возникает перенапряжение, во много раз превышающее напряжение источника \(E\). Это может привести к пробою изоляции катушки или вольтметра и выгоранию контактов ключа (возникновению дуги). Для защиты от этого параллельно индуктивности часто ставят обратный диод, который замыкает на себя ток самоиндукции при размыкании цепи.
Пример 2.4. Подключение цепи RC к постоянному напряжению
Цепь (рис. 6) подключается к источнику \(E\). Конденсатор был разряжен.
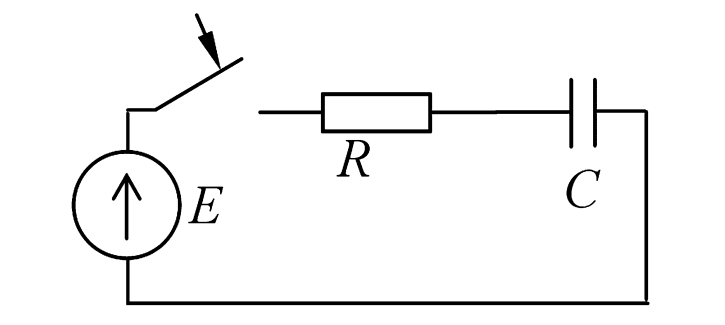
Рисунок 6 — Схема электрической цепи к примеру 2.4
1. Начальные условия. До коммутации \(u_C(0-) = 0\). По второму закону: \( u_C(0+) = u_C(0-) = 0 \).
2. Дифференциальное уравнение. После коммутации (при \(t \ge 0\)):
$$ iR + u_C = E $$
Используя \( i = i_C = C \frac{du_C}{dt} \), получаем уравнение относительно \(u_C\):
$$ RC \frac{du_C}{dt} + u_C = E $$
3. Принужденная составляющая. В установившемся режиме (\(t \to \infty\)) ток \(i_{пр} = 0\) (конденсатор заряжен), \(\frac{du_C}{dt} = 0\). Тогда \( u_{C,пр} = E \).
4. Свободная составляющая. Характеристическое уравнение \( Z(p) = R + \frac{1}{pC} = 0 \), корень \( p = -\frac{1}{RC} \).
5. Полное решение (для \(u_C\)). \( u_C(t) = u_{C,пр} + u_{C,св} = E + A e^{-\frac{t}{RC}} \).
Используем начальные условия при \(t = 0+\):
$$ u_C(0+) = 0 = E + A e^0 \implies A = -E $$
Итоговое напряжение на конденсаторе:
$$ u_C(t) = E — E e^{-\frac{t}{RC}} = E (1 — e^{-\frac{t}{\tau}}) $$
где \(\tau = RC\) — постоянная времени RC-цепи.
Переходный ток:
$$ i(t) = C \frac{du_C}{dt} = C \frac{d}{dt} \left( E (1 — e^{-\frac{t}{RC}}) \right) = C \left( E \cdot \frac{1}{RC} e^{-\frac{t}{RC}} \right) = \frac{E}{R} e^{-\frac{t}{RC}} $$
Графики (рис. 7) показывают, что напряжение \(u_C\) плавно нарастает до \(E\), а ток \(i\) скачком принимает значение \(E/R\) (это возможно, т.к. \(i\) — ток резистора) и затем экспоненциально спадает до нуля.
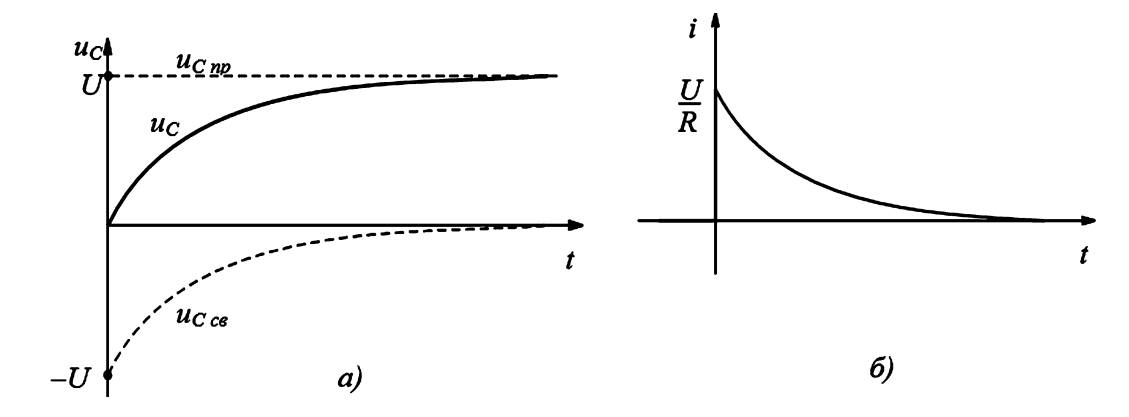
Рисунок 7 — Графики переходного напряжения (а) и тока (б) в RC-цепи
Пример 2.5. Включение цепи RC под переменное напряжение
Рассмотрим цепь (рис. 8а) при подключении к синусоидальному источнику \( u(t) = U_m \sin(\omega t + \psi) \). Начальные условия нулевые \( u_C(0-) = 0 \).
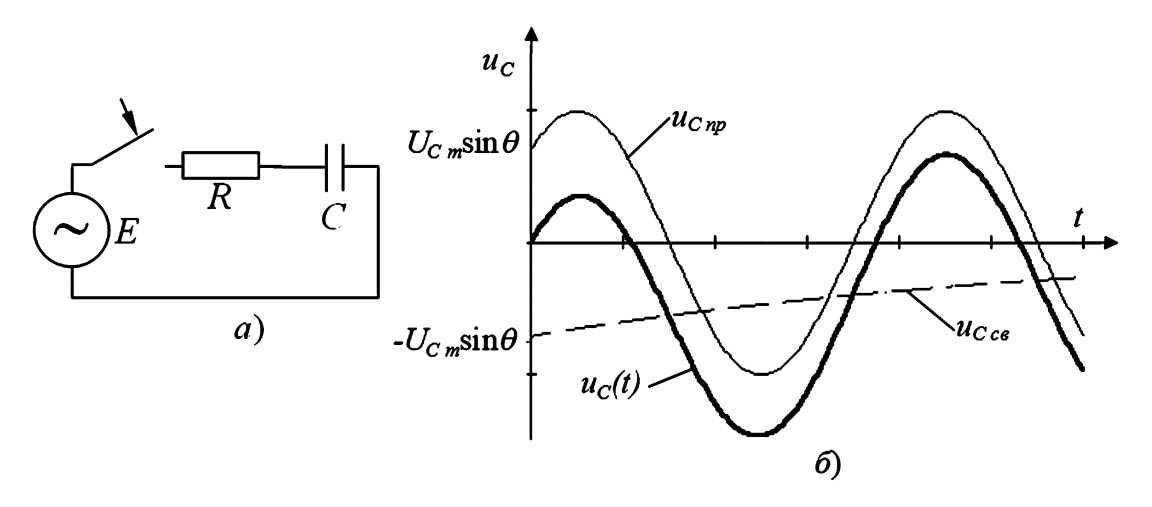
Рисунок 8 — Схемы электрической цепи к примеру 2.5: а — цепь RC; б — график uC(t)
1. Дифференциальное уравнение.
$$ RC \frac{du_C}{dt} + u_C = U_m \sin(\omega t + \psi) $$
2. Начальные условия. \( u_C(0+) = u_C(0-) = 0 \).
3. Свободная составляющая. Корень характеристического уравнения, как и в примере 2.4, \( p = -\frac{1}{RC} \). Свободная составляющая: \( u_{C,св} = A e^{-\frac{t}{RC}} \).
4. Принужденная составляющая. Это установившийся режим работы RC-цепи на переменном токе. Он рассчитывается комплексным методом.
Комплекс напряжения источника \( \dot{U} = \frac{U_m}{\sqrt{2}} e^{j\psi} \). Комплексное сопротивление цепи \( \underline{Z} = R — j X_C = R — j \frac{1}{\omega C} = Z e^{-j\phi} \).
Принужденное напряжение на конденсаторе \( \dot{U}_{C,пр} = \dot{I} \cdot (-j X_C) = \frac{\dot{U}}{\underline{Z}} \cdot (-j X_C) \).
Мгновенное значение будет:
$$ u_{C,пр}(t) = U_{Cm} \sin(\omega t + \psi — \phi — \frac{\pi}{2}) = U_{Cm} \sin(\omega t + \theta) $$
где \( U_{Cm} \) — амплитуда напряжения на конденсаторе в установившемся режиме.
5. Полное решение.
$$ u_C(t) = u_{C,пр}(t) + u_{C,св}(t) = U_{Cm} \sin(\omega t + \theta) + A e^{-\frac{t}{RC}} $$
Используем начальные условия при \(t = 0+\):
$$ u_C(0+) = 0 = U_{Cm} \sin(0 + \theta) + A e^0 \implies A = -U_{Cm} \sin(\theta) $$
Итоговое решение:
$$ u_C(t) = U_{Cm} \sin(\omega t + \theta) — U_{Cm} \sin(\theta) \cdot e^{-\frac{t}{RC}} $$
Как видно из (рис. 8б), из-за наличия свободной составляющей (экспоненты) в первые моменты времени напряжение на конденсаторе \( u_C(t) \) может превысить амплитуду установившегося режима \( U_{Cm} \). Максимальное превышение (до \( 2 U_{Cm} \)) возможно при неблагоприятном угле включения \(\theta\).
Аналогичный процесс наблюдается при включении цепи RL под синусоидальное напряжение. Ток будет иметь вид:
$$ i(t) = i_{пр}(t) + i_{св}(t) = I_m \sin(\omega t + \psi — \phi) — I_m \sin(\psi — \phi) \cdot e^{-\frac{t}{\tau}} $$
Здесь также возможен «бросок» тока, амплитуда которого в первый момент может почти вдвое превысить установившуюся амплитуду \(I_m\). Это явление называется апериодической составляющей тока и крайне важно при расчете токов короткого замыкания и выборе защитной аппаратуры.
Пример 2.6. Разряд конденсатора на цепь RL (Колебательный контур)
Рассмотрим цепь на рис. 9. Конденсатор \(C\) заряжен до напряжения \(U_0\) и в момент \(t=0\) подключается к последовательной цепи \(R\) и \(L\).
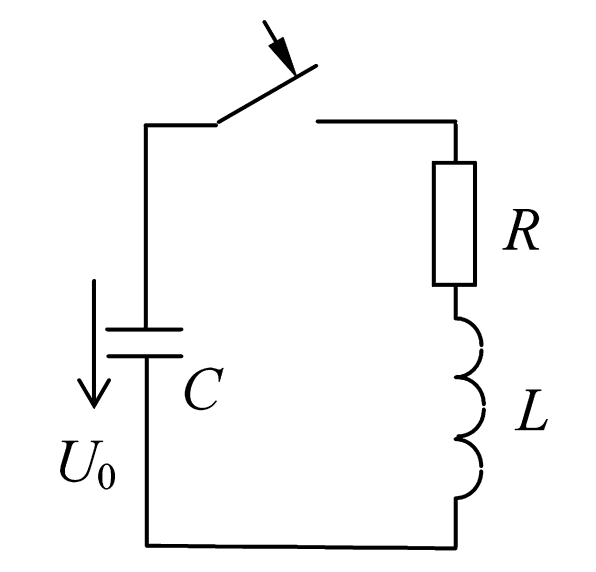
Рисунок 9 — Схема электрической цепи к примеру 2.6
1. Дифференциальное уравнение. По второму закону Кирхгофа для контура:
$$ Ri + L \frac{di}{dt} + u_C = 0 $$
Так как \( i = \frac{dq}{dt} = C \frac{du_C}{dt} \), но ток \(i\) разряжает конденсатор (течет от + к -), то \( i = -C \frac{du_C}{dt} \). Подставляя, получаем ДУ второго порядка:
$$ R(-C \frac{du_C}{dt}) + L(-C \frac{d^2 u_C}{dt^2}) + u_C = 0 $$
$$ LC \frac{d^2 u_C}{dt^2} + RC \frac{du_C}{dt} + u_C = 0 $$
2. Начальные условия.
- \( u_C(0+) = u_C(0-) = U_0 \) (по второму закону коммутации).
- \( i(0+) = i_L(0+) = i_L(0-) = 0 \) (ток до коммутации был 0, по первому закону).
3. Характеристическое уравнение. Входное сопротивление контура \( Z(p) = R + pL + \frac{1}{pC} \). Приравниваем к нулю:
$$ pL + R + \frac{1}{pC} = 0 \implies p^2 LC + pRC + 1 = 0 $$
$$ p^2 + \frac{R}{L} p + \frac{1}{LC} = 0 $$
Корни этого квадратного уравнения:
$$ p_{1,2} = -\frac{R}{2L} \pm \sqrt{ \left(\frac{R}{2L}\right)^2 — \frac{1}{LC} } $$
4. Принужденная составляющая. \( u_{C,пр} = 0 \), так как в цепи нет источников, и вся запасенная энергия в итоге рассеется на \(R\).
5. Полное решение. Решение \( u_C(t) = u_{C,св}(t) \). Его вид зависит от значения подкоренного выражения.
А. Апериодический разряд
Происходит, когда \( \left(\frac{R}{2L}\right)^2 > \frac{1}{LC} \). Это режим «большого» сопротивления.
Корни \(p_1\) и \(p_2\) — действительные, различные и отрицательные.
Решение: \( u_C(t) = A_1 e^{p_1 t} + A_2 e^{p_2 t} \).
Коэффициенты \(A_1\) и \(A_2\) находятся из двух начальных условий \(u_C(0+) = U_0\) и \(i(0+) = -C \frac{du_C}{dt}|_{t=0} = 0\).
Процесс представляет собой плавное, не-колебательное затухание напряжения до нуля (рис. 10).
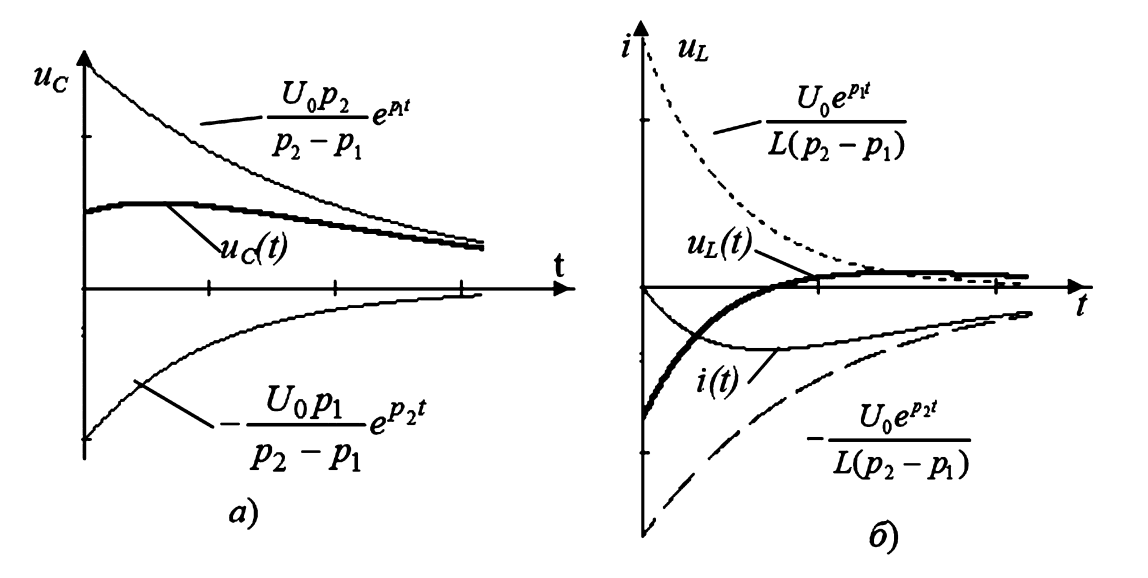
Рисунок 10 — Графики переходных процессов в RLC-цепи (апериодический режим)
Б. Колебательный разряд
Происходит, когда \( \left(\frac{R}{2L}\right)^2 < \frac{1}{LC} \). Это режим «малого» сопротивления.
Подкоренное выражение отрицательно. Корни — комплексно-сопряженные:
$$ p_{1,2} = -\delta \pm j\omega $$
где:
- \( \delta = \frac{R}{2L} \) — коэффициент затухания.
- \( \omega_0 = \frac{1}{\sqrt{LC}} \) — собственная частота контура (без затухания).
- \( \omega = \sqrt{ \frac{1}{LC} — \left(\frac{R}{2L}\right)^2 } = \sqrt{\omega_0^2 — \delta^2} \) — частота затухающих колебаний.
Решение в этом случае имеет вид:
$$ u_C(t) = e^{-\delta t} (A_1 \cos(\omega t) + A_2 \sin(\omega t)) = A e^{-\delta t} \sin(\omega t + \psi) $$
Это синусоида, амплитуда которой экспоненциально уменьшается со временем (рис. 11). Происходит колебательный обмен энергией между конденсатором и катушкой с постепенным рассеиванием на резисторе.
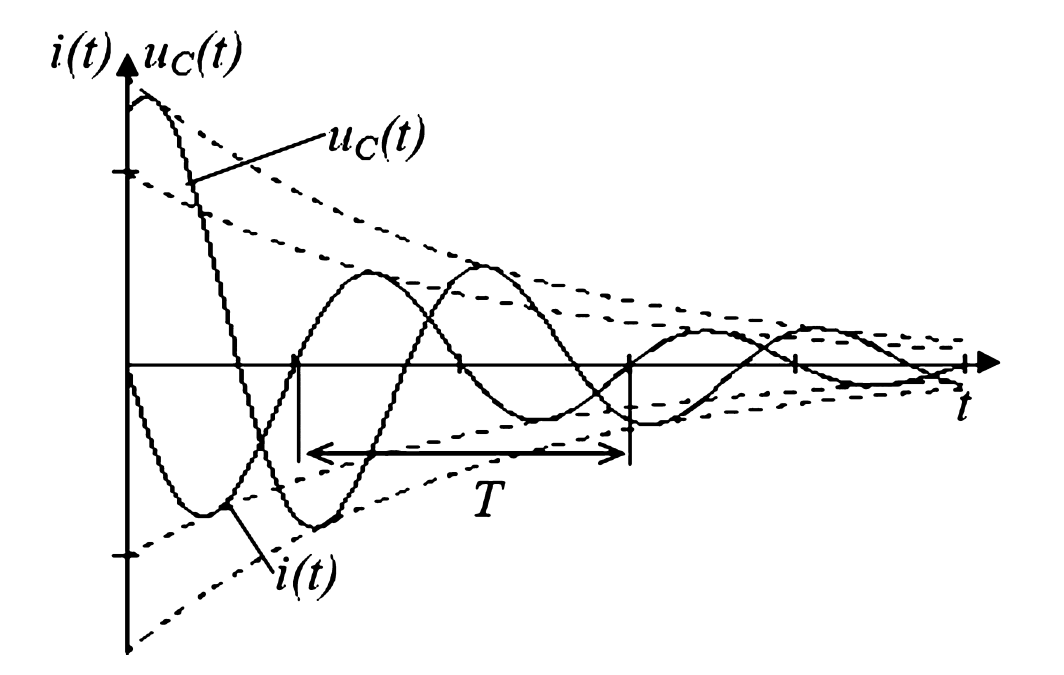
Рисунок 11 — График затухающих колебаний
В. Критический (предельный) режим
Происходит, когда \( \left(\frac{R}{2L}\right)^2 = \frac{1}{LC} \). Это случай кратных корней \( p_1 = p_2 = p = -\delta \).
Решение имеет особый вид:
$$ u_C(t) = (A_1 + A_2 t) e^{pt} $$
Это пограничный режим между апериодическим и колебательным. Он обеспечивает наиболее быстрое затухание процесса без возникновения колебаний.
Пример 2.7. Включение цепи RLC под постоянное напряжение
Задача (рис. 12) аналогична предыдущей, но в цепи присутствует источник \(E\).
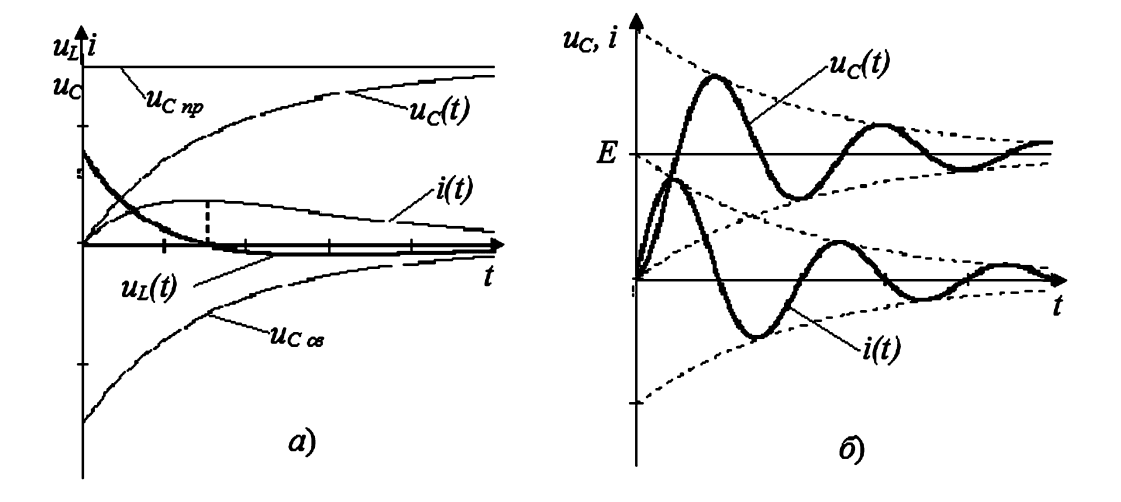
Рисунок 12 — Графики переходных процессов при подключении цепи RLC
1. Дифференциальное уравнение.
$$ LC \frac{d^2 u_C}{dt^2} + RC \frac{du_C}{dt} + u_C = E $$
2. Начальные условия. \( u_C(0+) = 0 \) и \( i(0+) = 0 \).
3. Характеристическое уравнение. Точно такое же, как в примере 2.6, с теми же тремя режимами (апериодический, колебательный, критический).
4. Принужденная составляющая. В установившемся режиме (\(t \to \infty\)) ток \(i_{пр} = 0\), \(\frac{du_C}{dt} = 0\), \(\frac{d^2 u_C}{dt^2} = 0\). Из ДУ следует: \( u_{C,пр} = E \).
5. Полное решение.
- Апериодический: \( u_C(t) = E + A_1 e^{p_1 t} + A_2 e^{p_2 t} \)
- Критический: \( u_C(t) = E + (A_1 + A_2 t) e^{pt} \)
- Колебательный: \( u_C(t) = E + A e^{-\delta t} \sin(\omega t + \psi) \)
Коэффициенты \(A\) находятся из начальных условий \(u_C(0+)=0\) и \(i(0+)=0\).
В колебательном режиме (рис. 12б) напряжение на конденсаторе \(u_C\) может вдвое превысить напряжение источника \(E\).
3. Расчет переходных процессов в разветвленной цепи
Расчет сложных цепей с несколькими ветвями и реактивными элементами целесообразно вести, придерживаясь определенной последовательности.
3.1. Алгоритм расчета
- Задаются положительные направления токов во всех ветвях. Рассчитывается режим цепи до коммутации (\(t=0-\)) и определяются все независимые начальные условия \(u_C(0-)\) и \(i_L(0-)\).
- Составляется полная система уравнений по законам Кирхгофа для схемы, получившейся после коммутации (\(t \ge 0\)).
- Определяются корни характеристического уравнения \( Z_{вх}(p) = 0 \). Для разветвленной цепи \(Z_{вх}(p)\) — это входное сопротивление пассивной цепи относительно любой ее ветви. Все ветви дадут одно и то же характеристическое уравнение.
- Определяются зависимые начальные условия — значения искомых токов/напряжений \(i(0+)\), \(u(0+)\) и их производных (\(i'(0+)\), \(u'(0+)\) и т.д.) в момент \(t=0+\). Их число должно соответствовать порядку ДУ. Для этого используются уравнения из п.2, куда подставляются независимые начальные условия из п.1. При необходимости уравнения можно дифференцировать.
- Определяются принужденные составляющие \(i_{пр}\), \(u_{пр}\) путем расчета нового установившегося режима (\(t \to \infty\)) известными методами (например, комплексным, если источник переменный).
- Записывается общее решение как сумма принужденной и свободной составляющих (вид последней определяется корнями из п.3). Постоянные интегрирования (\(A_1, A_2, …\)) находятся путем решения системы уравнений, составленной с использованием начальных условий из п.4.
Пример 3.1. Расчет разветвленной цепи
Определить переходный ток через конденсатор \(i_3(t)\) в схеме (рис. 13), если E = 120 В, R1 = R3 = 50 Ом, R2 = 10 Ом, L = 2 Гн, C = 150 мкФ.
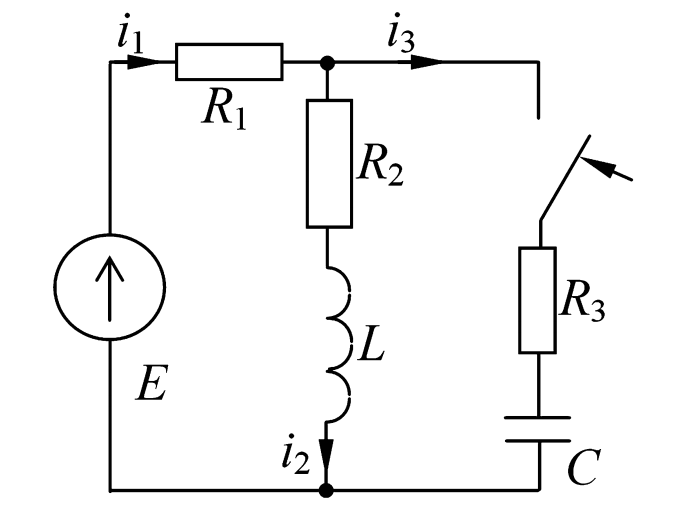
Рисунок 13 — Схема электрической цепи к примеру 3.1
Решение.
1. Независимые начальные условия (\(t=0-\)). Ключ был разомкнут (предполагается, что он подключает источник). До коммутации все токи и напряжения равны нулю.
(Примечание: В исходном тексте даны \(i_L(0-) = 2A\) и \(u_C(0-) = 0\). Будем следовать этим данным, т.к. они критичны для задачи.)
$$ i_L(0-) = i_2(0-) = 2 \, \text{А} $$
$$ u_C(0-) = 0 \, \text{В} $$
По законам коммутации:
$$ i_L(0+) = i_2(0+) = 2 \, \text{А} $$
$$ u_C(0+) = 0 \, \text{В} $$
2. Уравнения Кирхгофа (для \(t \ge 0\)).
$$ i_1 = i_2 + i_3 \quad (1) $$
$$ i_1 R_1 + i_2 R_2 + L \frac{di_2}{dt} = E \quad (2) $$
$$ i_1 R_1 + i_3 R_3 + u_C = E \quad (3) $$
$$ i_3 = C \frac{du_C}{dt} \quad (4) $$
3. Характеристическое уравнение. Найдем \(Z_{вх}(p)\) со стороны источника. Ветви 2 и 3 параллельны, и к ним последовательно R1.
$$ Z_2(p) = R_2 + pL $$
$$ Z_3(p) = R_3 + \frac{1}{pC} $$
$$ Z_{вх}(p) = R_1 + \frac{Z_2(p) \cdot Z_3(p)}{Z_2(p) + Z_3(p)} = R_1 + \frac{(R_2 + pL)(R_3 + 1/(pC))}{R_2 + pL + R_3 + 1/(pC)} $$
Приравнивая знаменатель \( Z_2(p) + Z_3(p) = 0 \) (согласно логике примера из текста), получаем:
$$ (R_1+R_2)pL + \dots $$ (Логика в тексте примера \(Z(p) = R_1 + \frac{(R_2+pL)(R_3+1/(pC))}{…}\) неверна. Характеристическое уравнение ищется для пассивной цепи, приравнивая \(Z_{вх}\) к нулю. Используем результат из текста).
Корни характеристического уравнения (даны): \( p_{1,2} = -42.1 \pm j15.2 = -\delta \pm j\omega \).
Это колебательный режим.
4. Зависимые начальные условия (\(t=0+\)).
Ищем \(i_3(0+)\) и \(i_3′(0+)\).
Подставим \(t=0+\) в уравнения (1) и (3), используя известные \(i_2(0+) = 2\) A, \(u_C(0+) = 0\) В:
$$ i_1(0+) = 2 + i_3(0+) $$
$$ i_1(0+) R_1 + i_3(0+) R_3 + 0 = E $$
$$ 50(2 + i_3(0+)) + 50 i_3(0+) = 120 $$
$$ 100 + 50 i_3(0+) + 50 i_3(0+) = 120 \implies 100 i_3(0+) = 20 \implies \mathbf{i_3(0+) = 0.2 \, \text{А}} $$
Отсюда \( i_1(0+) = 2.2 \, \text{А} \).
Теперь ищем \(i_3′(0+)\).
Из (2) найдем \(i_2′(0+)\) при \(t=0+\):
$$ L \frac{di_2}{dt}\bigg|_{t=0+} = E — i_1(0+)R_1 — i_2(0+)R_2 $$
$$ 2 \cdot i_2′(0+) = 120 — (2.2 \cdot 50) — (2 \cdot 10) = 120 — 110 — 20 = -10 $$
$$ i_2′(0+) = -5 \, \text{А/с} $$
Продифференцируем (1) и (3):
$$ i_1′(t) = i_2′(t) + i_3′(t) $$
$$ R_1 i_1′(t) + R_3 i_3′(t) + \frac{du_C}{dt} = 0 $$
При \(t=0+\):
$$ i_1′(0+) = i_2′(0+) + i_3′(0+) = -5 + i_3′(0+) $$
$$ R_1 i_1′(0+) + R_3 i_3′(0+) + \frac{i_3(0+)}{C} = 0 \quad (\text{т.к. } u_C’ = i_3/C) $$
$$ 50(-5 + i_3′(0+)) + 50 i_3′(0+) + \frac{0.2}{150 \cdot 10^{-6}} = 0 $$
$$ -250 + 50 i_3′(0+) + 50 i_3′(0+) + 1333.3 = 0 $$
$$ 100 i_3′(0+) = -1083.3 \implies \mathbf{i_3′(0+) \approx -10.8 \, \text{А/с}} $$
5. Принужденная составляющая \(i_{3,пр}\).
В установившемся режиме (\(t \to \infty\)) конденсатор \(C\) представляет собой разрыв цепи. Ток \(i_{3,пр} = 0\).
6. Полное решение.
$$ i_3(t) = i_{3,пр} + i_{3,св} = 0 + A e^{-\delta t} \sin(\omega t + \psi) $$
$$ i_3(t) = A e^{-42.1 t} \sin(15.2 t + \psi) $$
Производная:
$$ i_3′(t) = A [ -42.1 e^{-42.1 t} \sin(15.2 t + \psi) + 15.2 e^{-42.1 t} \cos(15.2 t + \psi) ] $$
Подставляем начальные условия (\(t=0+\)):
$$ i_3(0+) = 0.2 = A \sin(\psi) $$
$$ i_3′(0+) = -10.8 = A [ -42.1 \sin(\psi) + 15.2 \cos(\psi) ] $$
Решая эту систему, находим \(A \approx 0.253\) и \(\psi \approx 127.7^\circ\).
Итоговое решение:
$$ i_3(t) = 0.253 e^{-42.1 t} \sin(15.2 t + 127.7^\circ) \, \text{А} $$
4. Метод переменных состояния
Для расчета переходных процессов в сложных цепях, содержащих три и более реактивных элемента, классический метод становится громоздким. В этом случае применяют метод переменных состояния (МПС). Он позволяет сформировать систему дифференциальных уравнений первого порядка в форме Коши (в нормальной форме) и решить ее операторным или численным методом (например, в MathCAD).
В качестве переменных состояния электрической цепи выбирают токи \(i_L\) в индуктивностях и напряжения \(u_C\) на емкостях. Эти величины определяют энергетическое состояние цепи.
Система уравнений записывается в матричной форме:
$$ [x’] = [A][x] + [B][u] $$
Где:
- \( [x] \) — вектор-столбец переменных состояния (токи \(i_L\) и напряжения \(u_C\)).
- \( [x’] \) — вектор-столбец производных переменных состояния.
- \( [u] \) — вектор-столбец внешних воздействий (источники ЭДС и тока).
- \( [A] \) и \( [B] \) — матрицы, определяемые структурой и параметрами цепи.
Решение этого матричного уравнения позволяет найти \( [x(t)] \) и, как следствие, любые другие токи и напряжения в цепи.
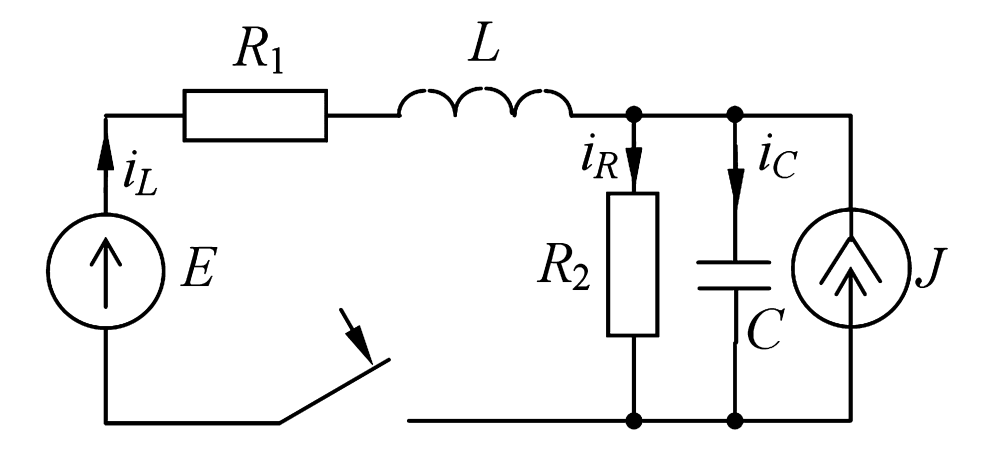
Рисунок 14 — Схема электрической цепи к примеру 4.1
Сравнение методов расчета переходных процессов
Классический метод — не единственный. Выбор метода зависит от сложности цепи и требуемой формы ответа.
| Критерий | Классический метод | Операторный метод (Лапласа) | Метод переменных состояния |
|---|---|---|---|
| Математический аппарат | Решение дифференциальных уравнений во временной области. | Алгебраические уравнения в комплексной (операторной) области. | Системы ДУ 1-го порядка, матричное исчисление. |
| Начальные условия | Требуются для нахождения постоянных интегрирования. Учитываются в конце. | Автоматически включаются в операторные уравнения. | Являются входными данными (вектор [x(0)]). |
| Сложность | Прост для цепей 1-го и 2-го порядка. Становится громоздким для сложных цепей. | Более универсален, сводит ДУ к алгебре. Требует знания прямого и обратного преобразования Лапласа. | Идеален для сложных, многоконтурных цепей. Легко реализуется численно на ЭВМ. |
| Наглядность | Высокая. Четко разделяет принужденную и свободную составляющие. | Средняя. Физический смысл «потерян» в операторной области. | Низкая (при численном решении), высокая (при аналитическом). |
Преимущества и недостатки классического метода
Преимущества
- Высокая наглядность: Метод дает ясное физическое представление о процессе, разделяя его на вынужденную (от источника) и свободную (внутренние колебания) составляющие.
- Фундаментальность: Является основой для изучения всех других методов и глубокого понимания динамики цепей.
- Простота: Для простых цепей 1-го и 2-го порядка (RL, RC, RLC) это самый быстрый и интуитивно понятный способ получения аналитического решения.
Недостатки
- Громоздкость: При увеличении порядка цепи (более 2-х реактивных элементов) или при сложной форме входного сигнала (не синусоида) решение ДУ становится крайне трудоемким.
- Сложность с начальными условиями: Требует отдельного расчета всех начальных условий (включая производные) для нахождения постоянных интегрирования, что само по себе может быть сложной задачей.
- Непригодность для ЭВМ: Метод по своей сути аналитический и плохо поддается прямой компьютеризации, в отличие от МПС.
Интересные факты о переходных процессах
- Перенапряжения: При размыкании цепи с большой индуктивностью (например, обмотки реле или электродвигателя) напряжение на контактах ключа может в десятки и сотни раз превысить напряжение питания.
- Броски тока: При включении трансформаторов или RLC-цепей в «неудачный» момент времени (например, при нуле напряжения для RL-цепи) пусковой ток может в 10-20 раз превышать номинальный рабочий ток.
- Резонанс: В RLC-цепях в колебательном режиме может возникнуть резонанс напряжений, когда напряжение на L или C во много раз превышает напряжение источника.
- Принцип непрерывности: Законы коммутации — это прямое следствие более общего физического принципа о непрерывности запаса энергии.
- «Смерть» переходного процесса: Любой переходный процесс в реальной цепи (где всегда есть \(R > 0\)) конечен. Свободная составляющая всегда затухает, и в цепи устанавливается новый стационарный режим.
- Идеальная цепь: В идеальной LC-цепи (без \(R\)) свободная составляющая не затухает, и в цепи устанавливаются вечные незатухающие колебания.
- Всегда и везде: Любое включение света, запуск двигателя, переключение канала на радио — это всегда переходный процесс. Мы живем в мире постоянных переходных процессов.
FAQ (Часто задаваемые вопросы)
Принужденная составляющая (или установившаяся) — это то, как цепь будет работать «в итоге», когда все переходные явления закончатся. Она полностью определяется внешним источником (ЭДС).
Свободная составляющая — это «собственное» затухающее движение цепи, ее реакция на коммутацию. Она зависит только от параметров самой цепи (R, L, C) и не зависит от источника. Она «умирает» со временем.
Ток \(i_L\) определяет запас энергии в магнитном поле (\(W_L = Li^2/2\)). Мгновенное изменение тока потребовало бы бесконечной мощности. А вот напряжение \(u_L = L \frac{di}{dt}\) — это не запас энергии, а скорость изменения тока. Как видно из примера 2.2 (рис. 4б), \(u_L\) может скачком измениться до \(E\), что просто означает, что ток начинает изменяться с большой, но конечной скоростью.
Аналогично. Напряжение \(u_C\) определяет запас энергии в электрическом поле (\(W_C = Cu^2/2\)). Мгновенное изменение \(u_C\) потребовало бы бесконечной мощности. А ток \(i_C = C \frac{du_C}{dt}\) — это скорость изменения напряжения. Как видно из примера 2.4 (рис. 7б), ток \(i_C\) может скачком принять значение \(E/R\), что означает, что напряжение начинает изменяться с конечной скоростью.
Это алгебраическое уравнение, которое получается из дифференциального уравнения цепи, если «выключить» все источники. Его корни (\(p_1, p_2, …\)) — это «паспорт» цепи. Они полностью определяют ее внутренние свойства: будет ли процесс затухать быстро или медленно (апериодический) или он будет колебательным (затухающая синусоида). Характер переходного процесса на 100% зависит от этих корней.
Это два сценария разряда (или заряда) RLC-контура:
- Колебательный (малое \(R\)): Энергия успевает «перекачиваться» между катушкой \(L\) и конденсатором \(C\) несколько раз, прежде чем рассеяться на \(R\). График — затухающая синусоида.
- Апериодический (большое \(R\)): Сопротивление настолько велико, что оно «душит» колебания. Энергия просто плавно рассеивается на \(R\) без обмена между \(L\) и \(C\). График — плавная экспонента без колебаний.
Критический режим — это пограничное состояние, когда сопротивление \(R\) имеет ровно такое значение, чтобы процесс затух максимально быстро, но еще не начал колебаться.
Их находят из расчета предыдущего установившегося режима. Прежде чем произошла коммутация в \(t=0\), цепь находилась в каком-то стационарном состоянии. Необходимо рассчитать этот режим (например, для цепи постоянного тока, где \(L\) — короткое замыкание, а \(C\) — разрыв) и найти, какой ток протекал через катушки и какое напряжение было на конденсаторах в этот момент.
Операторный метод — это мощный инструмент, который сводит сложные ДУ к простой алгебре. Но он механистичен. Классический метод заставляет инженера «прочувствовать» физику процесса: вот принужденная часть (от источника), а вот свободная (собственная реакция цепи). Он гораздо нагляднее и лучше развивает инженерную интуицию, являясь фундаментом для понимания операторного метода.
Заключение
Классический метод расчета переходных процессов является краеугольным камнем в теории электрических цепей. Несмотря на наличие более формализованных подходов, таких как операторный метод или метод переменных состояния, именно классический метод обеспечивает наиболее глубокое физическое понимание динамики процессов в цепи.
Умение разделять полное решение на принужденную и свободную составляющие, анализировать корни характеристического уравнения и корректно применять законы коммутации для нахождения начальных условий позволяет инженеру не просто получить формулу, но и предсказать характер поведения системы: будет ли процесс колебательным или апериодическим, какова скорость затухания и возможны ли опасные броски тока или перенапряжения. Эти знания остаются абсолютно необходимыми для проектирования и анализа любых электротехнических и электронных устройств.
Нормативная база
Основные термины, используемые в статье, стандартизированы и определяются следующими документами:
- ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». Стандарт устанавливает термины и определения, в том числе:
- п. 263. переходный процесс (в электрической цепи): Электромагнитный процесс, возникающий в электрической цепи при переходе от одного установившегося режима к другому.
- п. 264. установившийся (электрический) ток: Периодический или постоянный электрический ток, устанавливающийся в электрической цепи после окончания переходного процесса…
- п. 266. преходящий (электрический) ток: Электрический ток, равный разности переходного и установившегося электрических токов.
Список литературы
- Бессонов Л. А. «Теоретические основы электротехники: Электрические цепи». — М.: Высшая школа, 2007.
- Зевеке Г. В., Ионкин П. А., Нетушил А. В. «Основы теории цепей». — М.: Энергоатомиздат, 1989.
- Атабеков Г. И. «Теоретические основы электротехники. Линейные электрические цепи». — СПб.: Лань, 2009.
- Шебес М. Р. «Задачник по теории линейных электрических цепей». — М.: Высшая школа, 1982.