Энергия магнитного поля: определение, формулы и расчет

Содержание страницы

Плотность и общая формула энергии магнитного поля
Энергия в магнитных цепях с ферромагнитными сердечниками
Аспекты накопления магнитной энергии
Сравнение накопления магнитной энергии в разных материалах
Интересные факты о магнитной энергии
Часто задаваемые вопросы (FAQ)
Заключение

Энергия магнитного поля — это потенциальная энергия, накопленная в объеме пространства, где существует магнитное поле. Любой проводник с током, катушка индуктивности или постоянный магнит создают поле, которое содержит запасенную энергию. Эта концепция является фундаментальной в электротехнике и физике.

Исторически идея о том, что энергия хранится непосредственно в поле, а не в создающих его проводниках, была ключевым развитием в работах Майкла Фарадея и была математически оформлена Джеймсом Клерком Максвеллом в XIX веке. Эта концепция легла в основу его единой теории электромагнетизма и объясняет, как энергия может передаваться через пространство в виде электромагнитных волн.

Плотность и общая формула энергии магнитного поля

Магнитное поле, подобно электрическому, обладает энергией. Для ее количественной оценки вводится понятие объемной плотности энергии $w_м$, которое показывает, какой запас энергии приходится на единицу объема пространства.

В общем виде объемная плотность энергии в точке поля определяется через векторы магнитной индукции $\mathbf{B}$ (Тл) и напряженности $\mathbf{H}$ (А/м) как их скалярное произведение:

$$w_м = \frac{1}{2} (\mathbf{B} \cdot \mathbf{H})$$

Для линейной и изотропной среды, где векторы $\mathbf{B}$ и $\mathbf{H}$ сонаправлены и связаны через магнитную проницаемость $\mu$, формула упрощается:

$$w_м = \frac{1}{2} HB = \frac{1}{2} \mu H^2 = \frac{B^2}{2\mu}$$

Здесь $\mu = \mu_0 \mu_r$, где $\mu_0$ — магнитная постоянная ( $4\pi \cdot 10^{-7}$ Гн/м), а $\mu_r$ — относительная магнитная проницаемость среды. Единицы измерения физических величин и их определения стандартизированы, в частности, в ГОСТ 8.417-2002 «ГСИ. Единицы величин».

Полный запас магнитной энергии $W_м$ во всем объеме $V$, занимаемом полем, находится путем интегрирования объемной плотности по этому объему:

$$W_м = \int_V w_м \, dV = \frac{1}{2} \int_V HB \, dV \quad (1)$$

Эта формула является универсальной и применима для любого распределения поля в пространстве.

Энергия в магнитных цепях с ферромагнитными сердечниками

В практических расчетах магнитных цепей, таких как трансформаторы, дроссели или электромагниты, часто используются сердечники из ферромагнитных материалов (например, электротехническая сталь). Эти материалы, согласно ГОСТ 19693-74 «Материалы магнитные. Термины и определения», обладают высокой относительной магнитной проницаемостью ($\mu_r \gg 1$).

В таких цепях основная часть магнитного потока концентрируется внутри сердечника. При расчетах часто принимают допущение, что значения $H$ и $B$ несущественно меняются по сечению магнитопровода, то есть поле внутри сердечника однородно. При таком допущении интеграл в формуле (1) заменяется простым произведением:

$$W_м = \frac{1}{2} H B V \quad (2)$$

Здесь $V$ — полный объем ферромагнитного сердечника, в котором запасена энергия.

Пример: Магнитная цепь в виде тороида

Рассмотрим применение формулы для конкретной магнитной цепи, представленной на рис. 1. Это замкнутая цепь в форме тороида (кольца) с равномерно распределенной обмоткой.

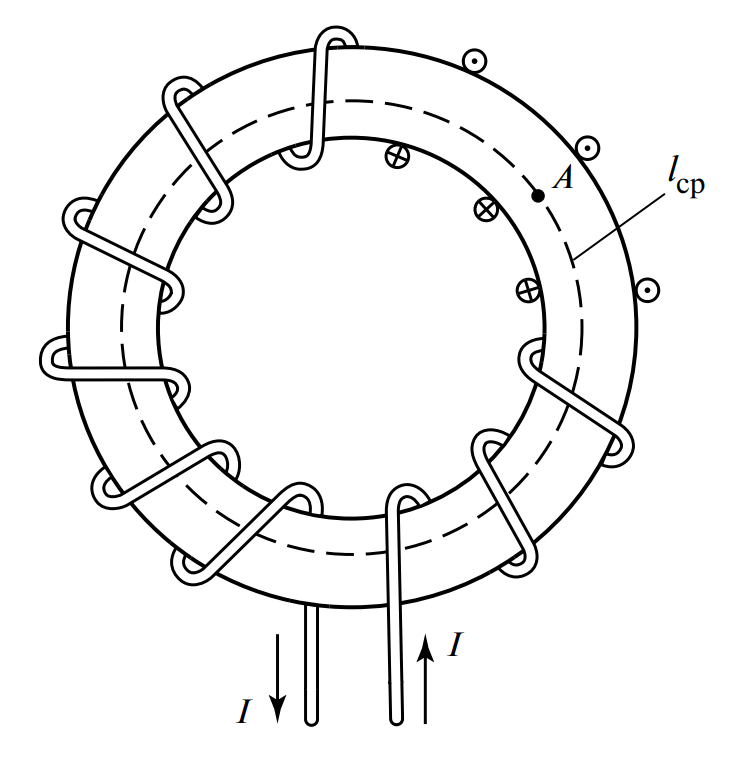
Рис. 1. Магнитная цепь в виде тороида

Для такой конфигурации принимаются следующие допущения:

Поле полностью сосредоточено внутри сердечника (потоками рассеяния пренебрегаем).
Поле равномерно распределено по всему сечению.

Введем обозначения:

$S$ — площадь поперечного сечения магнитопровода (м²).
$l_{ср}$ — средняя длина магнитной силовой линии (м).

Объем ферромагнитного сердечника в этом случае равен $V = S \cdot l_{ср}$.

Подставим это выражение для объема, а также связь $B = \mu_0 \mu_r H$ в формулу (2):

$$W_м = \frac{1}{2} H (\mu_0 \mu_r H) (S l_{ср})$$

После группировки членов получаем выражение для энергии магнитной цепи тороида:

$$W_м = \frac{1}{2} \mu_0 \mu_r H^2 S l_{ср} \quad (3)$$

Примечание: Из формулы (3) следует, что запасенная магнитная энергия прямо пропорциональна объему (а следовательно, и массе) ферромагнетика, его относительной магнитной проницаемости $\mu_r$ и, что особенно важно, квадрату напряженности магнитного поля $H^2$.

Зависимость от квадрата напряженности ($W_м \propto H^2$) или квадрата индукции ($W_м \propto B^2$) является ключевой. Это означает, что при увеличении напряженности поля в 2 раза, запасенная энергия увеличивается в 4 раза (при условии, что $\mu_r$ остается постоянной, то есть материал не вошел в насыщение).

Аспекты накопления магнитной энергии

Способность систем накапливать энергию в магнитном поле имеет как положительные, так и отрицательные аспекты в зависимости от применения.

Желательное накопление

Индуктивности и дроссели: Основная функция этих компонентов — накапливать энергию в магнитном поле и противодействовать резкому изменению тока. Эта энергия затем возвращается в цепь.
Электромагниты: Энергия поля используется для создания механической силы (например, в реле, контакторах, соленоидах, грузоподъемных магнитах).
Сверхпроводниковые индуктивные накопители (SMES): Эти системы используют сверхпроводимость для хранения огромного количества энергии в магнитном поле практически без потерь и могут выдавать ее с очень высокой мощностью.

Нежелательное накопление

Энергия полей рассеяния: В трансформаторах энергия, запасенная в полях рассеяния (магнитные линии, замыкающиеся по воздуху, а не по сердечнику), не участвует в передаче мощности и приводит к появлению реактивной мощности и падению напряжения.
Гистерезисные потери: Важно не путать запасенную энергию с рассеиваемой. При перемагничивании ферромагнитного сердечника переменным током часть энергии необратимо теряется, превращаясь в тепло. Эти потери на гистерезис за один цикл пропорциональны площади петли гистерезиса материала.

Сравнение накопления магнитной энергии в разных материалах

Способность вещества накапливать магнитную энергию напрямую зависит от его магнитной проницаемости $\mu_r$. По этому признаку все материалы делятся на три основные группы.

Тип материала	Относительная проницаемость ($\mu_r$)	Способность к накоплению энергии	Примеры
Диамагнетики	Чуть меньше 1 ($\mu_r < 1$)	Крайне низкая (незначительно ослабляют поле)	Вода, медь, висмут, сверхпроводники (в режиме Мейснера)
Парамагнетики	Чуть больше 1 ($\mu_r > 1$)	Очень низкая (незначительно усиливают поле)	Алюминий, платина, воздух, вольфрам
Ферромагнетики	Много больше 1 ($\mu_r \gg 1$)	Очень высокая (концентрируют и многократно усиливают поле)	Железо, никель, кобальт, электротехническая сталь, ферриты

Интересные факты о магнитной энергии

Энергия поля Земли: Наша планета обладает магнитным полем, генерируемым процессами в ее ядре. Это поле хранит колоссальный запас энергии, защищающий нас от солнечного ветра.
Энергия в вакууме: Магнитное поле хранит энергию даже в полном вакууме (где $\mu_r = 1$). Именно эта способность позволяет энергии в виде света и радиоволн путешествовать в космосе.
МРТ (Магнитно-резонансная томография): Аппараты МРТ используют сверхпроводящие магниты для создания чрезвычайно сильного и стабильного поля. Энергия, запасенная в этом поле, может быть огромной — эквивалентной энергии нескольких килограммов взрывчатки.
Потери на гистерезис: Площадь петли гистерезиса материала (графика B от H) имеет размерность энергии на единицу объема (Дж/м³). Она показывает, сколько энергии теряется в виде тепла за один цикл перемагничивания.
«Отдача» катушки: При резком размыкании цепи с индуктивностью запасенная в ее поле энергия ($W_м = LI^2/2$) высвобождается, создавая высоковольтный импульс (ЭДС самоиндукции). Это явление используется в системах зажигания, но может быть опасным для коммутационной аппаратуры.

Часто задаваемые вопросы (FAQ)

1. Где именно хранится магнитная энергия?

Энергия хранится не в проводниках с током и не в магнитах, а в самом пространстве, где существует магнитное поле. В магнитных цепях с сердечником большая часть этого пространства совпадает с объемом сердечника, так как он концентрирует поле в себе.

2. В чем разница между запасенной магнитной энергией и потерями на гистерезис?

Запасенная энергия — это потенциальная энергия поля (она обратима, ее можно вернуть в цепь). Потери на гистерезис — это энергия, которая необратимо рассеивается в виде тепла внутри ферромагнитного материала при его перемагничивании (работа, затраченная на «переориентацию» доменов).

3. Почему в формуле (3) используется $H^2$?

Это прямое следствие двух фактов: 1) плотность энергии пропорциональна произведению $H \cdot B$ и 2) для линейного материала $B$ само пропорционально $H$. Таким образом, $w_м \propto H \cdot ( \mu H ) \propto H^2$. Это показывает нелинейную (квадратичную) зависимость запаса энергии от силы поля.

4. Что такое «средняя длина силовой линии» $l_{ср}$?

Это эффективная длина, которую «проходит» магнитный поток внутри сердечника. Для простого тороида это длина окружности, проходящей через центр его сечения. В более сложных магнитных цепях (например, П- или Ш-образных) это расчетная величина, усредняющая длины разных участков потока.

5. Что такое магнитная постоянная $\mu_0$?

$\mu_0$ — это фундаментальная физическая константа, определяющая «силу» магнитных взаимодействий в вакууме. Она связывает единицы измерения электрических и магнитных величин, а также скорость света. Ее значение (согласно ГОСТ 8.417-2002) точно равно $4\pi \cdot 10^{-7}$ Гн/м.

Заключение

Энергия магнитного поля является фундаментальным понятием в электромагнетизме, описывающим энергию, запасенную в пространстве, где существует магнитное поле. Ее расчет критически важен для проектирования и анализа электротехнических устройств.

Ключевой вывод заключается в том, что количество запасенной энергии определяется тремя основными факторами: геометрией системы (объемом $V$), свойствами среды (магнитной проницаемостью $\mu$) и квадратом напряженности ($H^2$) или индукции ($B^2$) поля. Понимание этих зависимостей позволяет инженерам эффективно управлять накоплением и преобразованием энергии в трансформаторах, электродвигателях, индуктивностях и других магнитных системах.

Нормативная база

ГОСТ 19693-74 «Материалы магнитные. Термины и определения».
ГОСТ 8.417-2002 «Государственная система обеспечения единства измерений (ГСИ). Единицы величин».
ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий».
ГОСТ 12119.6-98 «Сталь электротехническая. Методы определения магнитных и электрических свойств. Определение магнитных свойств в постоянных полях методом баллистической установки».

Список литературы

Бессонов Л. А. Теоретические основы электротехники. Электромагнитное поле: Учебник для вузов. — М.: Гардарики, 2006.
Сивухин Д. В. Общий курс физики. Т. III. Электричество. — М.: Физматлит, 2009.
Калашников С. Г. Электричество: Учебное пособие. — М.: Физматлит, 2003.
Демирчян К. С., Нейман Л. Р., Коровкин Н. В. Теоретические основы электротехники: В 3-х т. Учебник для вузов. Том 2. — СПб.: Питер, 2009.