Электродинамические усилия в элементах аппаратов: Теория, расчет

Содержание страницы

1. Физическая природа электродинамических сил
2. Методы расчета электродинамических усилий
3. Электродинамические усилия в цепях переменного тока: динамика и переходные процессы
4. Сравнительный анализ методов расчета
5. Электродинамическая стойкость и проектирование: от теории к надежности
6. Интересные факты об электродинамических силах
7. Часто задаваемые вопросы (FAQ)
Заключение

Электродинамические усилия (ЭДУ) — это механические силы, возникающие между проводниками, по которым протекает электрический ток. Это фундаментальное явление электротехники, являющееся прямым следствием взаимодействия магнитного поля с движущимися электрическими зарядами. В контексте проектирования электрических аппаратов, ЭДУ — это критический фактор, определяющий надежность и безопасность оборудования.

Исторически изучение этих сил началось в 1820 году, когда Андре-Мари Ампер экспериментально установил закон механического взаимодействия двух токов. В дальнейшем, благодаря работам Майкла Фарадея и Джеймса Клерка Максвелла, теория электромагнитного поля получила математическое завершение, позволив инженерам точно рассчитывать нагрузки на токоведущие части.

В номинальных режимах работы эти силы, как правило, невелики и не вызывают деформаций. Однако при возникновении аварийных режимов, в частности коротких замыканий (КЗ) в энергосистемах большой мощности, токи могут возрастать в десятки и сотни раз. Так как сила пропорциональна квадрату тока, механические нагрузки возрастают лавинообразно, достигая значений в десятки тысяч ньютонов. Это способно разорвать шины, разбить изоляторы или сварить контакты. Поэтому расчет на электродинамическую стойкость является обязательным этапом проектирования любого силового электрооборудования.

1. Физическая природа электродинамических сил

Основой возникновения ЭДУ является магнитное поле. Любой проводник с током неизбежно создает вокруг себя магнитное поле. Если в это поле поместить второй проводник с током, то на него будет действовать сила Лоренца (в макроскопическом проявлении — сила Ампера). Таким образом, проводники взаимодействуют не напрямую, а через посредника — материальное магнитное поле.

Представьте два пожарных шланга, лежащих параллельно на земле. Когда по ним под огромным давлением пускают воду, они начинают «жить своей жизнью», изгибаясь и дергаясь. В электричестве роль давления играет ток, а роль упругости шланга — магнитное поле. Если токи текут в одну сторону — это подобно вакууму между шлангами, который их стягивает. Если навстречу — избыточное давление расталкивает их.

1.1 Основные правила определения направления сил

Для инженерной практики критически важно не только рассчитать величину силы, но и правильно определить её вектор. Для этого используются классические мнемонические правила:

Правило буравчика (правоходового винта): Позволяет определить направление вектора магнитной индукции \( \vec{B} \). Если поступательное движение винта совпадает с направлением тока, то вращение его рукоятки укажет ориентацию магнитных силовых линий.
Правило левой руки: Используется для нахождения направления самой силы. Если расположить левую ладонь так, чтобы линии магнитной индукции входили в неё, а четыре вытянутых пальца указывали направление тока, то отогнутый большой палец укажет направление действующей силы.

2. Методы расчета электродинамических усилий

В современной электротехнике выделяют два фундаментальных подхода к расчету ЭДУ. Выбор метода зависит от геометрии системы и доступности исходных данных.

2.1 Первый метод: Закон Ампера и Био-Савара-Лапласа

Этот метод является классическим «силовым» подходом. Он применяется, когда можно аналитически описать картину магнитного поля. Суть метода заключается в прямом интегрировании элементарных сил, действующих на участки проводника.

Рассмотрим базовый случай: два параллельных проводника длиной \( l_1 \) и \( l_2 \), находящихся на расстоянии друг от друга (см. Рисунок 1). Токи \( i_1 \) и \( i_2 \) направлены противоположно.

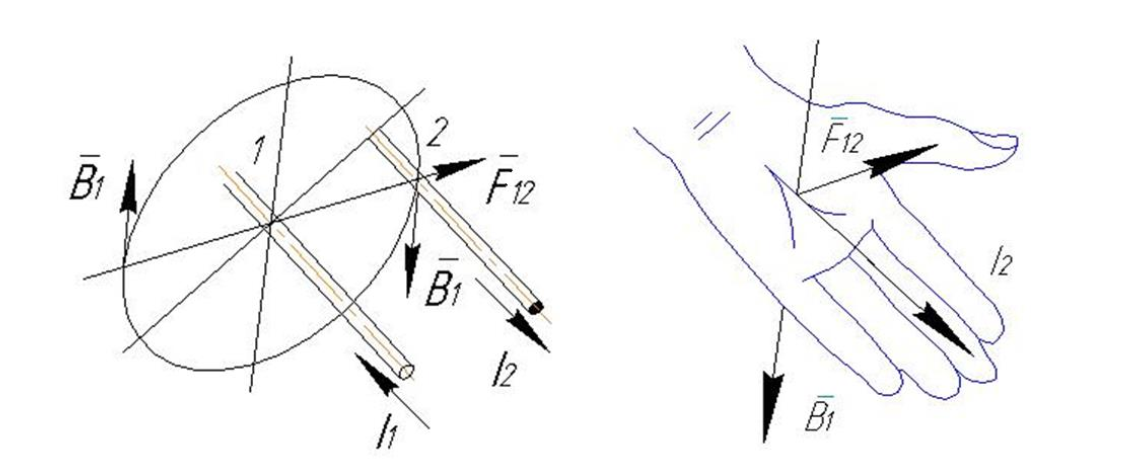
Рисунок 1 – Силовое взаимодействие двух проводников с токами и определение направления действия электромагнитной силы по «правилу левой руки». Вектор индукции B1 перпендикулярен плоскости проводников.

Согласно закону Ампера, на элементарный участок \( dl_2 \) проводника 2 действует сила \( dF_{12} \). Эта сила пропорциональна току и векторному произведению элемента длины на вектор магнитной индукции \( B_1 \), созданной первым проводником:

d\vec{F}_{12} = i_2 \cdot [d\vec{l}_2 \times \vec{B}_1]

В скалярной форме, учитывая угол \( \beta \) между вектором тока и вектором индукции:

dF_{12} = i_2 \cdot B_1 \cdot \sin\beta \cdot dl_2

Для большинства конструкций шинопроводов проводники параллельны и лежат в одной плоскости, следовательно, угол \( \beta = 90^\circ \), а \( \sin\beta = 1 \). Интегрируя по всей длине \( l_2 \), получаем полную силу:

F_{12} = \int_{0}^{l_2} B_1 \cdot i_2 \cdot dl_2

Метод академика В.Ф. Миткевича

Помимо классического векторного подхода, существует физически наглядный метод Миткевича, базирующийся на идеях Фарадея о «трубках» силового поля. Магнитным силовым линиям приписываются упругие свойства:

Боковой распор: Линии одного направления отталкиваются (как сжатые пружины бок о бок).
Продольное тяжение: Линии стремятся сократить свою длину (как растянутые резинки).

В примере на Рисунке 1, так как токи противоположны, магнитное поле между проводниками усиливается (линии «сгущаются»), создавая избыточное магнитное давление, которое расталкивает проводники. Проводник 2 испытывает силу вправо, проводник 1 — влево.

Детальный расчет для параллельных шин

Рассмотрим сложный случай взаимодействия проводников конечной длины (Рисунок 2).

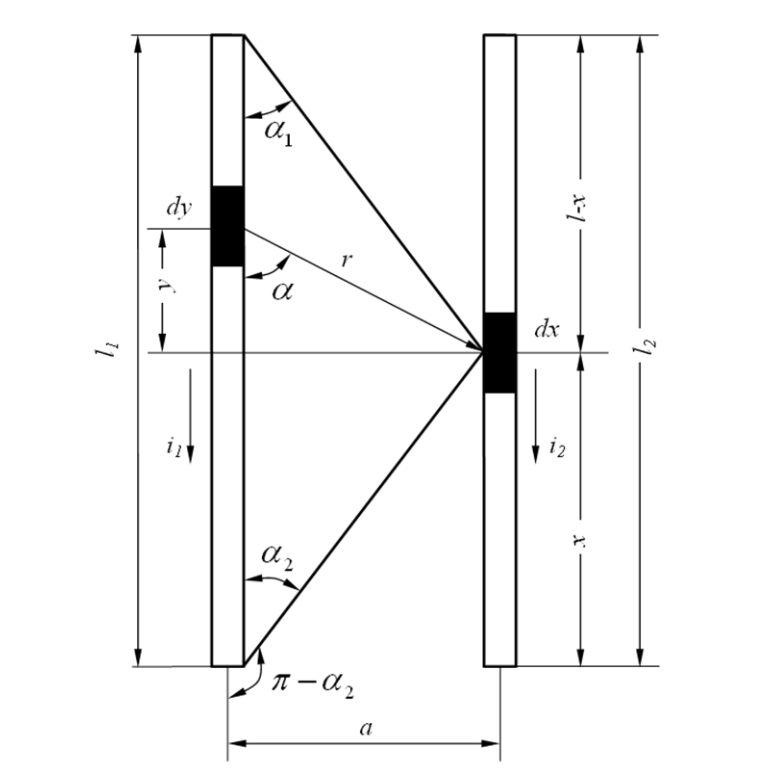
Рисунок 2 – Исходные данные для точного аналитического расчета ЭДУ между параллельными проводниками конечной длины. Показаны геометрические параметры для интегрирования.

Магнитная индукция \( dB_x \) в точке \( dx \) от элемента \( dy \) определяется законом Био-Савара-Лапласа:

dB_x = \frac{\mu_0 \cdot i_1 \cdot dy \cdot \sin\alpha}{4\pi \cdot r^2}

Здесь \( \mu_0 = 4\pi \cdot 10^{-7} \) Гн/м — магнитная постоянная вакуума. Этот фундаментальный параметр определяет «проницаемость» пространства для магнитного поля.

Процесс интегрирования требует замены переменных для упрощения (переход от линейных координат к угловым \( \alpha \)). После математических преобразований, включающих подстановку \( y = a / \text{tg}\alpha \) и взятие интеграла в пределах углов видимости проводника, мы получаем выражение для индукции \( B_x \):

B_x = \frac{\mu_0 \cdot i_1}{4\pi a} (\cos\alpha_1 + \cos\alpha_2)

Далее, подставляя это значение в формулу силы Ампера и выполняя вторичное интегрирование по длине второго проводника, мы приходим к итоговой формуле силы взаимодействия:

F = \frac{\mu_0}{4\pi} \cdot i_1 \cdot i_2 \cdot k_{\Gamma}

Где \( k_{\Gamma} \) — коэффициент геометрии:

k_{\Gamma} = \frac{2l}{a} \left( \sqrt{1 + (\frac{a}{l})^2} — \frac{a}{l} \right) \approx \frac{2l}{a} — 1 + …

Практическое упрощение: Если длина шин \( l \) значительно больше расстояния между ними \( a \) (т.е. \( a/l \ll 1 \), случай «бесконечно длинных шин»), сложная формула вырождается в простое выражение, известное каждому инженеру:

F = \frac{\mu_0}{2\pi} \cdot \frac{l}{a} \cdot i_1 \cdot i_2

Или в численном виде для практических расчетов:

F = 2 \cdot 10^{-7} \cdot i_1 \cdot i_2 \cdot \frac{l}{a} \cdot k_{\phi}

Здесь добавлен коэффициент формы \( k_{\phi} \).

Коэффициент формы \( k_{\phi} \) равен 1 только для круглых проводников (кабелей). Для прямоугольных шин, используемых в распределительных щитах, ток вытесняется к краям (поверхностный эффект и эффект близости), что меняет эффективное расстояние. Значения \( k_{\phi} \) берутся из справочных таблиц [7, 10].

2.2 Второй метод: Энергетический подход

Этот метод базируется на принципе виртуальных перемещений Лагранжа. Система токов обладает запасом электромагнитной энергии \( W \). Любая механическая сила в такой системе стремится изменить геометрию проводников так, чтобы эта энергия увеличилась (при условии постоянства токов).

F_x = \frac{\partial W}{\partial x}

Где \( x \) — обобщенная координата (расстояние, радиус, угол), в направлении которой мы ищем силу. Этот метод незаменим, когда сложно определить точное распределение индукции, но известна зависимость индуктивности \( L \) или взаимоиндуктивности \( M \) от геометрии.

Пример: Усилия в круговом витке (реакторе)

Рассмотрим виток радиусом \( R \) (Рисунок 3). Энергия витка:

W = \frac{1}{2} L \cdot i^2

Индуктивность витка зависит от его радиуса \( R \) и радиуса самого провода \( r \).

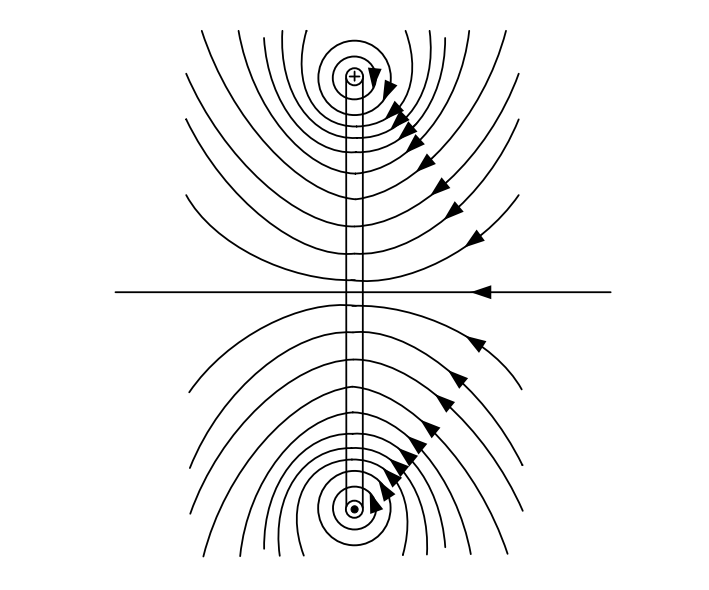
Рисунок 3 – Магнитное поле кругового витка. Силы бокового распора стремятся разорвать виток (увеличить R).

Внутри витка силовые линии сгущаются (см. Рисунок 3). Стремясь «распрямиться» и оттолкнуться друг от друга, они создают радиальное усилие, растягивающее виток. Дифференцируя выражение индуктивности по радиусу \( R \), получаем разрывающее усилие:

F_R = \frac{1}{2} i^2 \frac{d L}{d R}

Это усилие критично для токоограничивающих реакторов. При КЗ витки могут деформироваться, а изоляция — потрескаться.

Взаимодействие двух контуров

Для системы двух витков энергия включает энергию взаимоиндукции:

W = \frac{1}{2}L_1 i_1^2 + \frac{1}{2}L_2 i_2^2 + M i_1 i_2

Сила взаимодействия (притяжения или отталкивания) зависит от того, как меняется взаимоиндуктивность \( M \) при изменении расстояния \( h \) между витками:

F_h = i_1 i_2 \frac{d M}{d h}

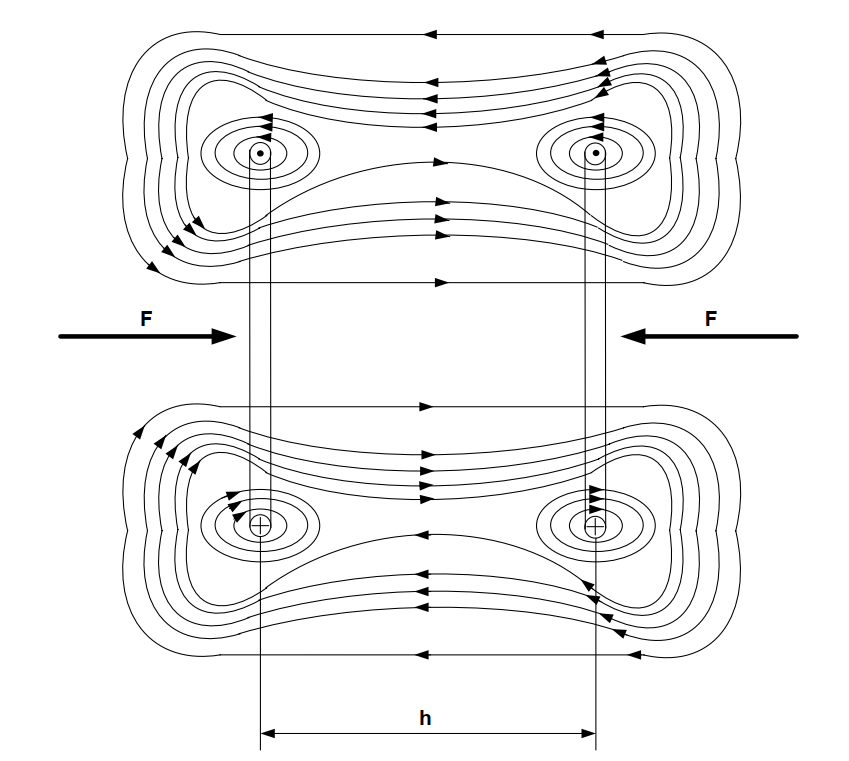
Рисунок 4 – Силовые линии магнитного поля двух витков с одинаковым током. Общий поток «стягивает» витки (продольное тяжение).

На Рисунке 4 показано, что при одинаковом направлении токов витки притягиваются (стремятся увеличить общий магнитный поток). Если токи встречные — они отталкиваются.

3. Электродинамические усилия в цепях переменного тока: динамика и переходные процессы

Переход от расчетов на постоянном токе (DC) к переменному (AC) требует смены парадигмы. В цепях постоянного тока сила, действующая на проводник, при неизменной геометрии постоянна во времени (\( F = const \)). Она создает статическую нагрузку, подобную весу груза.

В реальных энергосистемах, работающих на синусоидальном токе, электродинамическая сила превращается в сложную вибрационную нагрузку. Она пульсирует, меняет величину, а в многофазных системах — и направление. Это вносит критические коррективы в расчеты на усталостную прочность и динамическую устойчивость конструкций.

3.1 Однофазный ток и частота пульсаций

Рассмотрим физику процесса в однофазном контуре (или при двухфазном КЗ). Мгновенное значение силы \( f(t) \) всегда пропорционально квадрату мгновенного значения тока \( i(t) \). Если ток изменяется по гармоническому закону \( i = I_m \sin(\omega t) \), то уравнение силы принимает вид:

f(t) = c \cdot i^2 = c \cdot I_m^2 \sin^2(\omega t)

Используя тригонометрическое тождество понижения степени \( \sin^2\alpha = \frac{1 — \cos 2\alpha}{2} \), мы можем разложить эту силу на две составляющие:

f(t) = \underbrace{\frac{c I_m^2}{2}}_{\text{Постоянная составляющая}} — \underbrace{\frac{c I_m^2}{2} \cos(2\omega t)}_{\text{Гармоническая составляющая}}

Анализ уравнения:

Частотный спектр: Сила содержит переменную составляющую, изменяющуюся с двойной частотой \( 2\omega \). Для стандартной сети 50 Гц это означает, что шины испытывают 100 механических ударов в секунду.
Знакопостоянство: В однофазной цепи (например, два параллельных провода с током «туда и обратно») токи всегда направлены противоположно друг другу. Несмотря на то, что ток меняет направление, он меняет его в обоих проводниках одновременно. Минус на минус дает плюс. Поэтому сила всегда является отталкивающей. Она пульсирует от нуля до максимума, но никогда не тянет проводники друг к другу.
Амплитудный рост: Максимальное значение силы \( F_{max} \) достигается, когда \( \cos(2\omega t) = -1 \). В этот момент \( f(t) = c I_m^2 \). Если сравнить это с постоянным током, равным действующему значению переменного (\( I = I_m / \sqrt{2} \)), то пиковая сила на переменном токе будет ровно в 2 раза выше.

Представьте, что вы забиваете гвоздь. Постоянный ток — это если бы вы положили молоток на шляпку и давили всем весом. Переменный ток — это серия быстрых ударов молотком. Даже если среднее давление одинаково, разрушительная способность ударов (вибрации) значительно выше из-за пиковых нагрузок.

3.2 Ударный ток короткого замыкания: физика худшего сценария

Наибольшую опасность для оборудования представляет не установившийся режим КЗ, а переходный процесс в момент коммутации. В первые периоды времени возникает так называемый ударный ток.

Почему это происходит?
Любая электрическая цепь обладает индуктивностью \( L \). Фундаментальный закон коммутации гласит: ток в индуктивности не может измениться скачком. Энергия магнитного поля \( W = Li^2/2 \) должна накапливаться плавно.

Если замыкание происходит в момент, когда напряжение сети проходит через ноль (\( u \approx 0 \)), то в установившемся режиме чисто индуктивной цепи ток должен был бы быть максимальным (сдвиг фаз 90°). Но ток не может прыгнуть с нуля до максимума. Чтобы компенсировать этот скачок, в цепи возникает апериодическая (свободная) составляющая постоянного тока, которая затухает по экспоненте.

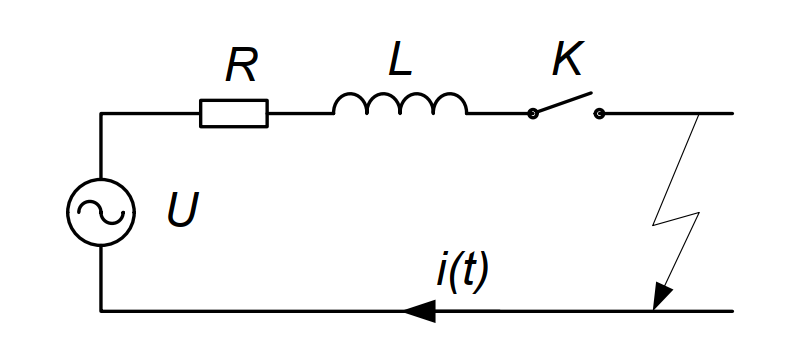
Рисунок 5 — Схема замещения участка цепи для определения переходного тока короткого замыкания.

Рисунок 6 — Формирование ударного тока. Апериодическая слагающая \( i_{ap} \) смещает ось симметрии синусоиды, создавая асимметрию и гигантский первый пик.

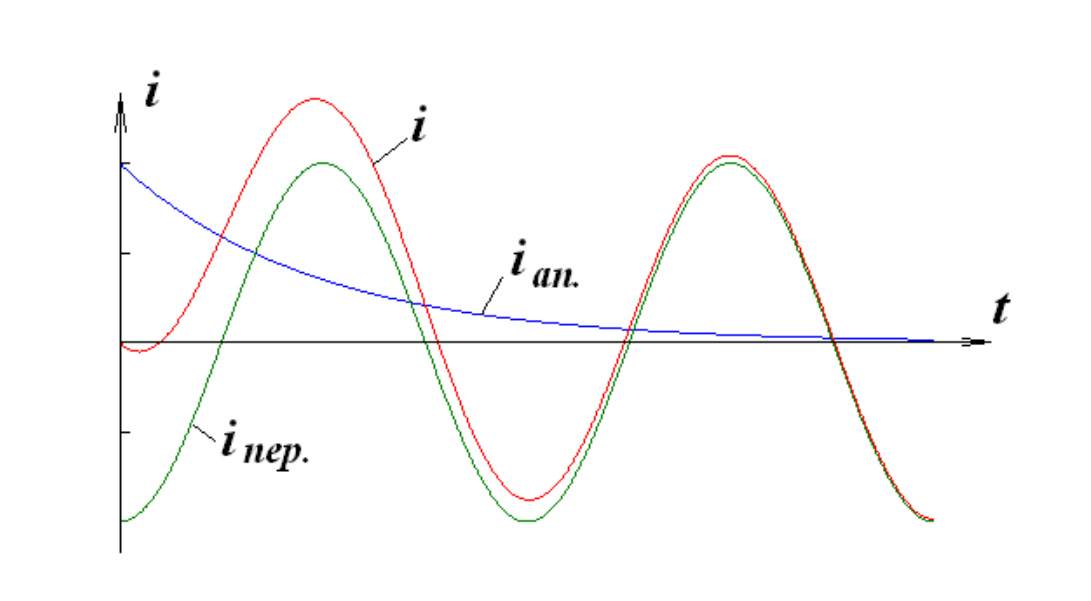
Уравнение полного тока КЗ:

i(t) = \underbrace{I_m \sin(\omega t + \psi)}_{\text{Вынужденная (Периодическая)}} + \underbrace{I_{ap0} e^{-t/T_a}}_{\text{Свободная (Апериодическая)}}

Максимальный мгновенный ток (ударный ток \( i_{ud} \)) достигается примерно через полпериода (0.01 с) после начала аварии. Его величина рассчитывается через ударный коэффициент:

i_{ud} = \sqrt{2} \cdot I_{po} \cdot k_{ud}

Где:

\( I_{po} \) — действующее значение периодической составляющей тока в начальный момент.
\( k_{ud} \) — ударный коэффициент, зависящий от постоянной времени затухания цепи \( T_a = L/R \).Теоретический максимум \( k_{ud} = 2 \) (в цепи без сопротивления, \( R=0 \)).Реальный расчетный максимум для сетей высокого напряжения принимается 1.8.Для сетей низкого напряжения (где велико активное сопротивление R) \( k_{ud} \approx 1.1…1.3 \).

Квадратичный эффект усиления силы

Поскольку сила зависит от квадрата тока, даже небольшое увеличение тока приводит к лавинообразному росту нагрузок. Рассчитаем коэффициент перегрузки для стандартного случая (\( k_{ud} = 1.8 \)):

F_{max} \propto i_{ud}^2 = (\sqrt{2} \cdot 1.8 \cdot I_{po})^2 = 2 \cdot 3.24 \cdot I_{po}^2 = 6.48 \cdot I_{po}^2

Вывод: Если вы рассчитаете шины просто по номинальному току КЗ, не учитывая ударный эффект, реальная сила окажется в 6.5 раз больше расчетной. Это гарантированное разрушение конструкции.

3.3 Трехфазные системы: векторное взаимодействие

В трехфазной системе (шины фаз A, B, C расположены в одной плоскости) картина сил значительно сложнее из-за фазового сдвига токов на 120°.

Силы, действующие на среднюю фазу (Фаза B):
Средняя шина находится в поле двух крайних (A и C).

В любой момент времени сумма токов \( i_A + i_B + i_C = 0 \) (для трехфазного КЗ).
Если ток в фазе B максимален, то токи в фазах A и C направлены в противоположную сторону и равны половине амплитуды.
Это означает, что обе крайние шины одновременно отталкивают среднюю шину.

В отличие от однофазной системы, в трехфазной сила является знакопеременной.

— Когда токи совпадают по направлению — шины притягиваются.

— Когда токи встречные — отталкиваются.

В результате средняя шина испытывает не просто пульсирующее сжатие, а полноценную вибрацию «вперед-назад», проходящую через ноль. Это создает условия для раскачивания и механического резонанса.

Максимальное усилие на среднюю фазу при ударном токе трехфазного КЗ рассчитывается по формуле:

F_{max}^{(3)} = \frac{\sqrt{3}}{2} \cdot 2 \cdot 10^{-7} \cdot i_{ud}^2 \cdot \frac{l}{a} \cdot k_{rasp}

Множитель \( \frac{\sqrt{3}}{2} \approx 0.866 \) появляется из-за векторного сложения сил от двух соседних фаз, сдвинутых по времени. Несмотря на то, что этот коэффициент меньше единицы, средняя фаза все равно остается наиболее нагруженной по сравнению с крайними, так как она испытывает воздействие с двух сторон.

Для крайних фаз сила несколько меньше, и ее вектор направлен преимущественно наружу от центральной шины, но она также пульсирует с частотой сети.

4. Сравнительный анализ методов расчета

Для удобства выбора метода при проектировании, сведем их характеристики в таблицу.

Характеристика	Метод закона Ампера (Био-Савара)	Энергетический метод
Физическая основа	Прямое взаимодействие токов и полей (векторная алгебра).	Закон сохранения энергии, принцип виртуальных перемещений.
Область применения	Линейные проводники, шинопроводы, простые контуры.	Сложные контуры, катушки, реакторы, электромагниты, системы сложной формы.
Сложность	Требует сложного векторного интегрирования для непараллельных участков.	Требует знания аналитической формулы индуктивности. Дифференцирование обычно проще интегрирования.
Точность	Высокая для тонких проводников. Требует поправок (коэф. формы) для шин.	Зависит от точности формулы индуктивности. Хорошо учитывает объемные эффекты.
Основное преимущество	Наглядность вектора силы в каждой точке.	Универсальность для замкнутых систем.

5. Электродинамическая стойкость и проектирование: от теории к надежности

Проектирование высоковольтных и низковольтных аппаратов невозможно без тщательного анализа их электродинамической стойкости. Это не просто способность «не сломаться», а комплексное свойство конструкции сохранять свою геометрию, изоляционные промежутки и функциональность после протекания сквозных токов короткого замыкания (КЗ).

В современной инженерии различают понятия статической и динамической устойчивости конструкции. При КЗ ударная нагрузка прикладывается внезапно (импульсно), что вызывает в материале шин и изоляторов сложные волновые процессы деформации. Поэтому расчет как для «статической балки» часто дает заниженные результаты, требуя введения специальных динамических коэффициентов.

5.1 Критерии проверки и нормативная база (ГОСТ)

Основой для проверки оборудования в РФ является ГОСТ Р 52735-2007 «Короткие замыкания в электроустановках. Методы расчета электродинамического и термического действия тока короткого замыкания».

Проверка аппарата считается успешной, если выполняются условия механической прочности. Для этого сравниваются расчетные параметры сети (максимально возможные в точке установки) с паспортными данными оборудования, полученными в ходе типовых испытаний.

Условия электродинамической стойкости: 1. По пиковому значению тока: \( i_{dyn} \geq i_{shock} \) 2. По действующему значению (для аппаратов с малым временем протекания): \( I_{dyn} \geq I_{shock\_rms} \)

Где:

\( i_{dyn} \) — номинальный ток электродинамической стойкости (амплитудное значение). Это предел, который гарантирует производитель.
\( i_{shock} \) — ударный ток КЗ в цепи. Рассчитывается с учетом апериодической составляющей, которая зависит от момента замыкания и постоянной времени сети \( T_a \).

Физический смысл критерия: Механические напряжения \( \sigma \), возникающие в материале токоведущих частей (меди или алюминии), не должны превышать допустимых значений \( \sigma_{dop} \).

Для жестких шин допустимое напряжение обычно принимается близким к пределу текучести материала (например, для меди М1Т \( \sigma_{0.2} \approx 250 \) МПа, допустимое \( \sigma_{dop} \approx 140…160 \) МПа).
Допускаются небольшие остаточные деформации, если они не нарушают изоляционных расстояний и не препятствуют движению подвижных контактов.

5.2 Механический расчет шинных конструкций

Шинопровод рассматривается как многопролетная балка, лежащая на опорах (изоляторах). Под действием распределенной электродинамической нагрузки \( q \) возникает изгибающий момент \( M \).

Максимальное механическое напряжение в материале шины определяется по формуле:

\sigma = \frac{M_{max}}{W} = \frac{F \cdot l}{m \cdot W}

Где:

\( M_{max} \) — максимальный изгибающий момент (Н·м);

\( W \) — момент сопротивления сечения шины (м³). Для прямоугольной шины сечением \( b \times h \) (изгиб поперек \( h \)): \( W = \frac{b h^2}{6} \);

\( l \) — длина пролета между изоляторами;

\( m \) — коэффициент, зависящий от способа закрепления (для шарнирного опирания \( m=8 \), для жесткой заделки \( m=12 \)).

Обратите внимание: напряжение \( \sigma \) растет пропорционально квадрату длины пролета \( l^2 \) (так как сила \( F \) сама зависит от длины). Поэтому уменьшение расстояния между изоляторами является самым эффективным способом повышения электродинамической стойкости.

5.3 Проблема механического резонанса

Статический расчет, приведенный выше, справедлив только если частота собственных колебаний шины далека от частоты возмущающей силы. В цепях переменного тока промышленной частоты \( f_{network} = 50 \) Гц электродинамическая сила пульсирует с удвоенной частотой \( 2\omega = 100 \) Гц.

Шина, закрепленная на изоляторах, представляет собой механическую колебательную систему (аналог струны). Её собственная частота \( f_{mech} \) зависит от жесткости материала и геометрии:

f_{mech} = \frac{\alpha}{l^2} \sqrt{\frac{E \cdot J}{S \cdot \gamma}}

Где:

\( E \) — модуль упругости Юнга (для меди \( 1.1 \cdot 10^{11} \) Па);

\( J \) — момент инерции сечения;

\( S \) — площадь сечения;

\( \gamma \) — плотность материала.

Опасность резонанса: Если \( f_{mech} \) попадает в диапазон \( 95…105 \) Гц (или кратные гармоники), наступает явление механического резонанса. Амплитуда колебаний шины начинает неограниченно возрастать, даже если сама сила КЗ невелика.

Это приводит к эффекту «хлыста»:

Разрушаются опорные изоляторы (на срез или разрыв головки).
Происходит схлестывание шин соседних фаз (переход в двух- или трехфазное КЗ).
Возникает усталостное разрушение металла в местах крепления.

Для учета динамики в расчеты вводится коэффициент динамической реакции \( \eta \). При совпадении частот \( \eta \) может достигать значений 3…5 и более. Проектировщики обязаны «отстраиваться» от резонанса, подбирая длину пролета \( l \) так, чтобы \( f_{mech} \) была либо значительно ниже (гибкие шины), либо значительно выше (жесткие короткие шины) частоты 100 Гц.

5.4 Электродинамические силы в контактных группах

Контакт — это самое уязвимое место аппарата. Даже при идеальной обработке поверхности, электрический контакт осуществляется не по всей площади, а через микроскопические выступы — «пятна касания».

Рисунок 7 — Эффект стягивания линий тока (стрикция) в переходном контакте.

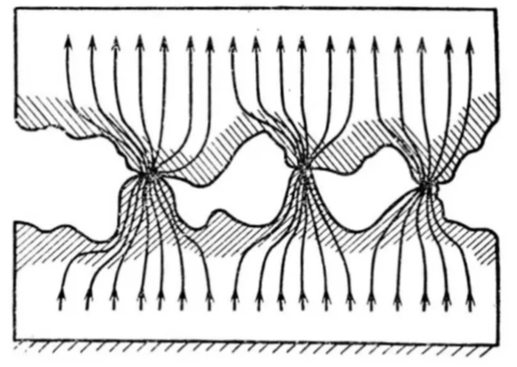
Из-за резкого искривления линий тока, стремящихся пройти через узкое пятно контакта, возникают мощные силы отталкивания. Это явление описывается формулой Хольма для силы электродинамического отброса:

F_{otbr} = \frac{\mu_0 \cdot i^2}{4\pi} \ln\left( \frac{D}{2a} \right)

Где:

\( D \) — диаметр контактов;

\( a \) — радиус пятна касания (зависит от силы нажатия и твердости материала).

Сценарий аварии:

Если сила отброса \( F_{otbr} \) превысит силу контактной пружины \( F_{pr} \), контакты на мгновение разомкнутся («подпрыгнут»). В образовавшемся зазоре возникнет электрическая дуга. Так как ток КЗ огромен, дуга мгновенно расплавит металл контактов, и при последующем падении тока они сварятся между собой. Аппарат потеряет способность к коммутации.

Методы борьбы с отбросом контактов

Чтобы предотвратить аварию, конструкторы используют сами электродинамические силы для защиты аппарата.

Электродинамические компенсаторы (Петлевой эффект): Токоведущий контур формируют в виде петли (U-образно). Токи в параллельных ветвях петли текут в разные стороны и, согласно законам электродинамики, отталкиваются. Однако, геометрия подвижного контакта устроена так, что это отталкивание шин превращается в прижимающее усилие в зоне контактов.
Это работает как «электромагнитный замок»: чем больше ток аварии, тем сильнее «челюсти» контакта сжимаются, не давая дуге возникнуть.
Дробление контактов: Вместо одной массивной пары используют несколько параллельных «пальцев» (ламелей). Поскольку токи в параллельных ламелях текут в одну сторону, они притягиваются друг к другу (эффект пинча), создавая дополнительное боковое давление и увеличивая трение, что препятствует отбросу.
Увеличение предварительного нажатия: Использование мощных тарельчатых пружин и рычажных механизмов для создания высокого начального давления \( P_{nach} \), уменьшающего переходное сопротивление и увеличивающего радиус пятна касания \( a \).

6. Интересные факты об электродинамических силах

Рельсотрон (Railgun).
Это оружие будущего работает исключительно на принципах электродинамических усилий. Снаряд, являющийся частью цепи, разгоняется силой Лоренца между двумя параллельными шинами (рельсами) до скоростей, превышающих 2 км/с (6 Махов), без использования пороха.
Эффект пинча.
При протекании сверхсильных токов через газоразрядную плазму или расплавленный металл, электродинамические силы сжатия становятся настолько велики, что шнур тока самопроизвольно сжимается в тонкую нить. Этот эффект используется в установках термоядерного синтеза (токамаках) для удержания плазмы.
Мгновенная сварка.
При коротком замыкании на шинопроводах сила сжатия в точке контакта может достигать тысяч килограммов. Если контакты недостаточно массивны, они могут свариться друг с другом за доли секунды, превратив разборное соединение в монолит.
Бесшумные субмарины.
Магнитогидродинамический (МГД) двигатель использует электродинамическую силу для перемещения морской воды (которая является проводником) через канал внутри корабля. Это позволяет субмаринам двигаться без вращающихся винтов, что делает их практически невидимыми для сонаров.
Космическая праща.
Электродинамические тросы (tethers) — это длинные проводники, развернутые со спутников. Взаимодействуя с магнитным полем Земли, они могут создавать тягу для изменения орбиты аппарата или генерировать электричество без расхода топлива.
Жидкий металл.
В ядерных реакторах на быстрых нейтронах для перекачки радиоактивного жидкого натрия используют электромагнитные насосы. В них нет движущихся частей (лопастей), а металл толкает сама электродинамическая сила, возникающая при пропускании тока через теплоноситель в магнитном поле.
Гудение трансформаторов.
Характерный звук работающей подстанции вызван явлением магнитострикции и электродинамическими усилиями в обмотках. При частоте сети 50 Гц силы пульсируют с частотой 100 Гц, заставляя витки катушек и листы сердечника вибрировать и «стучать» друг о друга.

7. Часто задаваемые вопросы (FAQ)

Почему при коротком замыкании кабели могут «подпрыгивать»?

Это происходит из-за резкого возникновения электродинамических сил отталкивания. Если кабель лежит на полу или лотке и по нему протекает ток КЗ, а рядом проходит возвратный провод (или земля), возникают силы, стремящиеся расширить контур тока. При ударных токах в десятки килоампер эта сила способна подбросить тяжелый кабель в воздух и сорвать его с креплений.

Что опаснее для оборудования: термическое или электродинамическое действие тока?

Оба фактора критичны, но действуют в разное время. Электродинамическое разрушение происходит мгновенно (в первые 0.01–0.02 с) в момент удара тока. Термическое разрушение (расплавление изоляции или проводника) требует времени для нагрева. Если аппарат не выдержит динамического удара, он разрушится еще до того, как успеет перегреться.

Зачем нужны шинные компенсаторы?

Шинные компенсаторы (обычно в виде пакета гибких тонких пластин) нужны не только для компенсации теплового расширения металла, но и для гашения вибраций, вызванных электродинамическими силами переменного тока. Они предотвращают передачу механических усилий на изоляторы, защищая их от растрескивания.

Почему средняя фаза в трехфазной системе страдает больше всех?

В плоской системе шин средняя фаза (обычно фаза B) находится между двумя другими. При трехфазном КЗ на нее действуют силы отталкивания и притяжения одновременно с двух сторон. В результате векторного сложения сил нагрузка на среднюю шину оказывается примерно на 15–20% выше, чем на крайние фазы.

Можно ли использовать электродинамические силы во благо?

Да, инженеры научились это делать. Например, в автоматических выключателях используются системы магнитного дутья: электродинамическая сила сама выталкивает электрическую дугу в дугогасительную камеру, ускоряя её гашение. Также эти силы используются в электроизмерительных приборах (амперметрах) и динамиках аудиосистем.

Заключение

Расчет электродинамических усилий — это сложная междисциплинарная задача, объединяющая электромагнитную теорию поля, теоретическую механику и сопротивление материалов. Понимание физики процессов (взаимодействие полей, ударные токи, резонанс) позволяет инженерам создавать надежные энергетические системы. Игнорирование этих явлений может привести к катастрофическим авариям с разрушением дорогостоящего оборудования.

Современные методы, включая конечно-элементное моделирование (FEM), базируются на описанных выше фундаментальных принципах (Ампера и Энергетическом), делая их изучение обязательным для любого специалиста-электротехника.

Нормативная база

ГОСТ Р 52735-2007 — Короткие замыкания в электроустановках. Методы расчета электродинамического и термического действия тока короткого замыкания.

Список литературы

Чунихин А.А. Электрические аппараты: общий курс. Учебник для вузов. — 3-е изд., перераб. и доп. — М.: Энергоатомиздат, 1988. — 720 с.
Правила устройства электроустановок (ПУЭ). Издание 7. Глава 1.4 «Выбор электрических аппаратов и проводников по условиям короткого замыкания». — Утв. Минэнерго РФ. —