Теория и расчет пассивных и активных электрических фильтров

Содержание страницы

1. Реактивные фильтры
2. Активные фильтры
3. Сравнительная характеристика типов фильтров
4. Интересные факты о фильтрах
5. Часто задаваемые вопросы (FAQ)
Заключение

Частотный электрический фильтр — это устройство (представляемое в теории как четырехполюсник), предназначенное для селекции (отбора) сигналов в определенном диапазоне частот. Идеальный фильтр пропускает сигналы в заданной полосе (зоне прозрачности) без ослабления и полностью подавляет сигналы за ее пределами (в зоне затухания).

В теории цепей, фильтром называют такой четырехполюсник, у которого в определенной полосе частот коэффициент затухания $a = 0$, а в остальной полосе $a > 0$. Полосу частот, в которой $a = 0$ (и, соответственно, напряжения на входе и выходе $U_1 = U_2$), называют зоной прозрачности. Все остальные частоты образуют зону затухания. Частоты, разделяющие эти зоны, называют частотами среза (обозначаются $\omega_c$).

Исторически, основы теории пассивных фильтров были заложены в начале XX века работами Джорджа Кэмпбелла (George Campbell) и Отто Зобеля (Otto Zobel) из AT&T, которые разработали фильтры типа k и m для нужд телефонной связи.

Классификация частотных фильтров

По расположению зоны прозрачности фильтры делятся на:

Низкочастотные (ФНЧ): зона прозрачности в области $0 < \omega < \omega_c$.
Высокочастотные (ФВЧ): зона прозрачности в области $\omega_c < \omega < \infty$.
Полосовые (ПФ): зона прозрачности в области $\omega_{c1} < \omega < \omega_{c2}$.
Заграждающие (ЗФ) или режекторные: зоны прозрачности $0 < \omega < \omega_{c1}$ и $\omega_{c2} < \omega < \infty$.

По элементной базе фильтры бывают реактивные (LC), безындуктивные (RC), активные (с усилительными элементами), пьезоэлектрические, электромеханические и другие.

1. Реактивные фильтры

Определим условия, при которых симметричный четырехполюсник, состоящий из минимального количества реактивных элементов (индуктивностей L и емкостей C), будет функционировать как фильтр. Такие элементы обладают чисто мнимым (реактивным) сопротивлением и в идеале не потребляют активной мощности.

Возможны две основные симметричные схемы таких четырехполюсников: Т-образная (Рис. 1а) и П-образная (Рис. 1б). Обе они могут быть получены путем каскадного соединения двух несимметричных Г-образных звеньев (Рис. 1в). Чтобы сохранить эту взаимосвязь, параметры сопротивлений на схемах заданы соответствующим образом (Z1 разделено на Z1/2, а Z2 представлено как проводимость 1/Z2 или два параллельных сопротивления 2Z2).

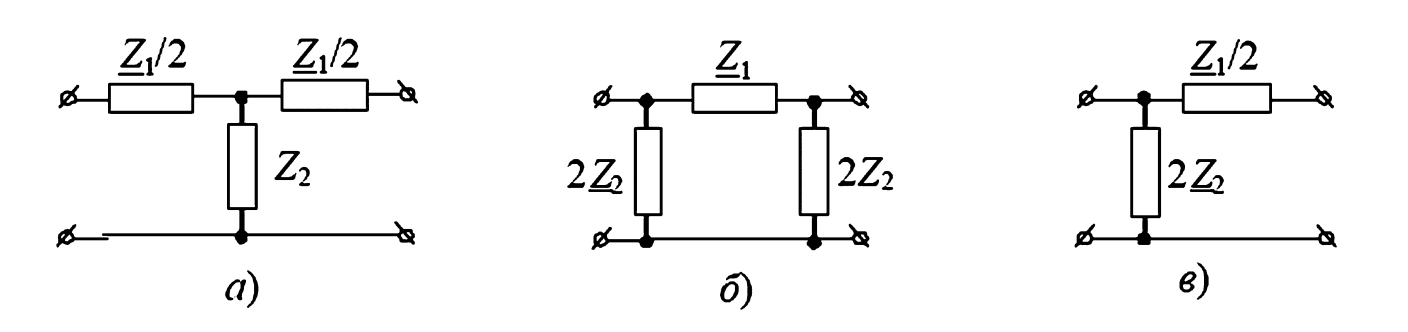
Рис. 1. Схемы реактивных фильтров: а — Т-образная; б — П-образная; в — Г-образная.

Четырехполюсник будет фильтром, если его коэффициент затухания $a = 0$ для некоторой полосы частот. Рассмотрим Т-образную схему (Рис. 1а). Для нее коэффициент передачи $g$ (называемый также постоянной передачи) в режиме холостого хода или короткого замыкания связан с параметрами схемы через гиперболический косинус:

$$
\cosh(g) = A = \frac{U_{1xx}}{U_{2xx}} = 1 + \frac{Z_1}{2Z_2}
$$

Где $g = a + jb$, $a$ — коэффициент затухания, $b$ — коэффициент фазы.

Распишем левую часть по формуле Эйлера для гиперболических функций:

$$
\cosh(a + jb) = \cosh(a)\cos(b) + j \sinh(a)\sin(b)
$$

Приравнивая это к правой части, получаем комплексное уравнение:

$$
\cosh(a)\cos(b) + j \sinh(a)\sin(b) = 1 + \frac{Z_1}{2Z_2} \quad (1)
$$

Поскольку мы рассматриваем реактивный фильтр, сопротивления $Z_1$ и $Z_2$ являются чисто мнимыми (например, $Z_1 = jX_1$ и $Z_2 = jX_2$). Это значит, что их отношение $Z_1 / Z_2$ всегда является вещественным числом. Следовательно, вся правая часть уравнения (1) является вещественным числом. Это позволяет нам приравнять мнимую часть левой части к нулю, а вещественную — к правой части. Уравнение (1) распадается на два:

$$
\cosh(a)\cos(b) = 1 + \frac{Z_1}{2Z_2} \quad (1а)
$$
$$
\sinh(a)\sin(b) = 0 \quad (1б)
$$

Анализ зоны прозрачности

В зоне прозрачности по определению $a = 0$. При этом $\sinh(a) = \sinh(0) = 0$ и $\cosh(a) = \cosh(0) = 1$.
Уравнение (1б) выполняется автоматически ($0 \cdot \sin(b) = 0$).
Уравнение (1а) принимает вид:

$$
\cos(b) = 1 + \frac{Z_1}{2Z_2}
$$

Известно, что функция $\cos(b)$ может принимать значения только в диапазоне от –1 до 1. Следовательно, зона прозрачности существует только для тех частот, где выполняется условие:

$$
-1 \le 1 + \frac{Z_1}{2Z_2} \le 1
$$

Вычитая 1 из всех частей, получаем фундаментальное условие для зоны прозрачности:

$$
-2 \le \frac{Z_1}{2Z_2} \le 0
$$

Это условие может выполняться, только если сопротивления $Z_1$ и $Z_2$ имеют разный характер (разные знаки реактивности), то есть одно является индуктивным ($j\omega L$), а другое — емкостным ($-j / (\omega C)$). В этом случае их отношение $Z_1 / Z_2 = (j\omega L) / (-j / (\omega C)) = -\omega^2 LC$ будет вещественным и отрицательным, что и требуется.

Границами зоны прозрачности будут частоты, где $\frac{Z_1}{2Z_2} = 0$ или $\frac{Z_1}{2Z_2} = -2$ (т.е. $Z_1 = -4Z_2$).

В этой зоне коэффициент фазы $b$ определяется из:

$$
\cos(b) = 1 + \frac{Z_1}{2Z_2} \quad \text{или} \quad \sin^2\left(\frac{b}{2}\right) = \frac{1 — \cos(b)}{2} = — \frac{Z_1}{4Z_2}
$$
$$
\sin\left(\frac{b}{2}\right) = \sqrt{-\frac{Z_1}{4Z_2}} \quad (2)
$$

Анализ зоны затухания

В зоне затухания $a \neq 0$, следовательно, $\sinh(a) \neq 0$.
Чтобы уравнение (1б) $\sinh(a)\sin(b) = 0$ выполнялось, необходимо, чтобы $\sin(b) = 0$. Это возможно при $b = 0$ или $b = \pm\pi$.

Если $b = 0$, то $\cos(b) = 1$. Уравнение (1а) дает $\cosh(a) = 1 + \frac{Z_1}{2Z_2}$. В зоне затухания $\frac{Z_1}{2Z_2}$ выходит за пределы $[-2, 0]$. Если $Z_1$ и $Z_2$ разного знака, то $\frac{Z_1}{2Z_2}$ отрицательно, и при $\frac{Z_1}{2Z_2} < -2$ (например, -3), $\cosh(a)$ было бы отрицательным, что невозможно. Если $\frac{Z_1}{2Z_2} > 0$ (одинаковый тип реактивностей), то $\cosh(a) > 1$, что соответствует затуханию, но не создает зоны прозрачности. Поэтому для фильтров, у которых $Z_1$ и $Z_2$ разного типа, решение $b=0$ не используется.
Остается только одно решение: в зоне затухания $b = \pm\pi$. При этом $\cos(b) = -1$.

Подставив $b = \pm\pi$ в уравнение (1а), получаем:

$$
\cosh(a) \cdot (-1) = 1 + \frac{Z_1}{2Z_2}
$$
$$
\cosh(a) = -1 — \frac{Z_1}{2Z_2} = -\left(1 + \frac{Z_1}{2Z_2}\right) \quad (3)
$$

Это выражение корректно, так как в этой зоне $\left(1 + \frac{Z_1}{2Z_2}\right)$ меньше чем -1, и $\cosh(a)$ будет больше 1.

Ключевые выводы по реактивным фильтрам:

Фильтр должен состоять из реактивных элементов разного типа (L и C).
Зона прозрачности ($a=0$): $-2 \le \frac{Z_1}{2Z_2} \le 0$. Фаза $b$ изменяется.
Зона затухания ($a > 0$): $\frac{Z_1}{2Z_2} < -2$. Фаза $b$ постоянна и равна $\pm\pi$.

Характеристическое сопротивление

Характеристическое (волновое) сопротивление $Z_c$ является важным параметром для согласования фильтра с нагрузкой. Для Т-образной схемы оно равно:

$$
Z_{CT} = \sqrt{Z_1 Z_2 + \frac{Z_1^2}{4}} = \sqrt{Z_1 Z_2 \left(1 + \frac{Z_1}{4Z_2}\right)}
$$

Для П-образной схемы:

$$
Z_{C\Pi} = \frac{Z_1 Z_2}{Z_{CT}} = \frac{Z_1 Z_2}{\sqrt{Z_1 Z_2 + \frac{Z_1^2}{4}}} = \frac{\sqrt{Z_1 Z_2}}{\sqrt{1 + \frac{Z_1}{4Z_2}}}
$$

Введем параметр номинального характеристического сопротивления $k = \sqrt{Z_1 Z_2}$. Поскольку $Z_1$ и $Z_2$ — реактивности разного знака, их произведение $Z_1 Z_2 = (j\omega L)(-j/(\omega C)) = L/C$ является вещественным, положительным и постоянным (не зависит от частоты!). Такие фильтры называют фильтрами типа k (постоянного k).

Выражение $1 + \frac{Z_1}{4Z_2}$ в зоне прозрачности (где $-2 \le \frac{Z_1}{2Z_2} \le 0$) изменяется от 0 до 1. Это означает, что в зоне прозрачности $Z_c$ является чисто активным (вещественным) сопротивлением. В зоне затухания $Z_c$ становится чисто реактивным.

Характеристическое сопротивление $Z_c$ в зоне прозрачности изменяется при изменении частоты:

У Т-образного фильтра: от 0 до $k$.
У П-образного фильтра: от $k$ до $\infty$.

1.1. Низкочастотный фильтр (ФНЧ) типа k

Для создания фильтра низких частот (ФНЧ) необходимо, чтобы $a = 0$ было в полосе $0 < \omega < \omega_c$. Условие $Z_1/(2Z_2) = 0$ должно выполняться при $\omega = 0$. Это достигается, если $Z_1$ — индуктивность, а $Z_2$ — емкость.

Продольное сопротивление: $Z_1 = j\omega L$ (равно 0 при $\omega = 0$)
Поперечное сопротивление: $Z_2 = 1 / (j\omega C) = -j / (\omega C)$ (бесконечно при $\omega = 0$)

На другой границе зоны (частоте среза $\omega_c$) выполняется условие $Z_1 = -4Z_2$:

$$
j\omega_c L = -4 \left( \frac{1}{j\omega_c C} \right) = \frac{4j}{\omega_c C}
$$
$$
\omega_c^2 LC = 4 \quad \Rightarrow \quad \omega_c = \frac{2}{\sqrt{LC}}
$$

На Рисунке 2 представлены Т- и П-образные схемы ФНЧ.

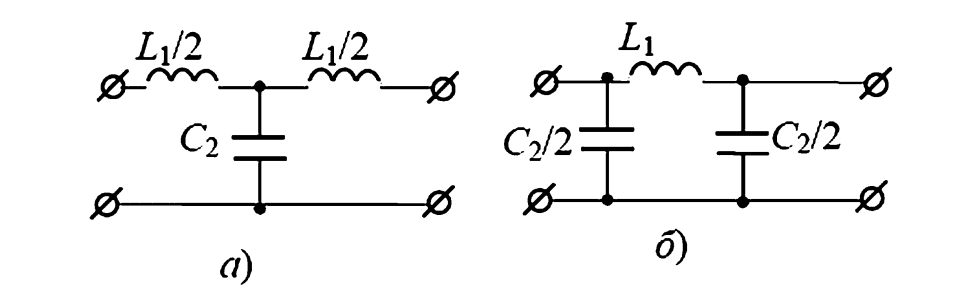
Рис. 2. Схемы низкочастотных фильтров типа k: а — Т-образная; б — П-образная.

На Рисунке 3 показаны частотные зависимости параметров ФНЧ. Коэффициент затухания $a$ равен нулю до $\omega_c$ и резко растет после. Коэффициент фазы $b$ линейно растет до $\pi$, а затем остается постоянным. Характеристическое сопротивление $Z_c$ (Рис. 3в) сильно изменяется в зоне прозрачности. Из-за этого согласовать нагрузку с фильтром можно только на одной частоте. Обычно сопротивление нагрузки $R_н$ принимают равным номинальному $k = \sqrt{L/C}$.

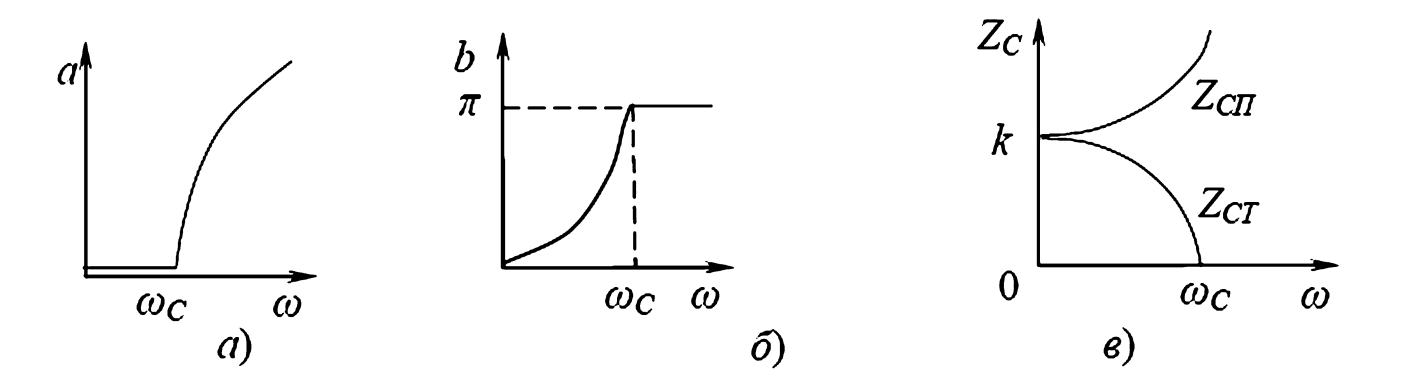
Рис. 3. Зависимости от частоты для ФНЧ типа k: а — коэффициента затухания; б — коэффициента фазы; в — характеристического сопротивления.

1.2. Высокочастотный фильтр (ФВЧ) типа k

Для фильтра высоких частот (ФВЧ) необходимо, чтобы $a = 0$ при $\omega_c < \omega < \infty$. Условие $Z_1/(2Z_2) = 0$ должно выполняться при $\omega = \infty$. Это достигается, если $Z_1$ — емкость, а $Z_2$ — индуктивность.

Продольное сопротивление: $Z_1 = 1 / (j\omega C) = -j / (\omega C)$
Поперечное сопротивление: $Z_2 = j\omega L$

На частоте среза $\omega_c$ также выполняется $Z_1 = -4Z_2$:

$$
\frac{1}{j\omega_c C} = -4 (j\omega_c L) = \frac{4 \omega_c L}{j}
$$
$$
1 = 4 \omega_c^2 LC \quad \Rightarrow \quad \omega_c = \frac{1}{2\sqrt{LC}}
$$

На Рисунке 4 представлены схемы и графики параметров ФВЧ.

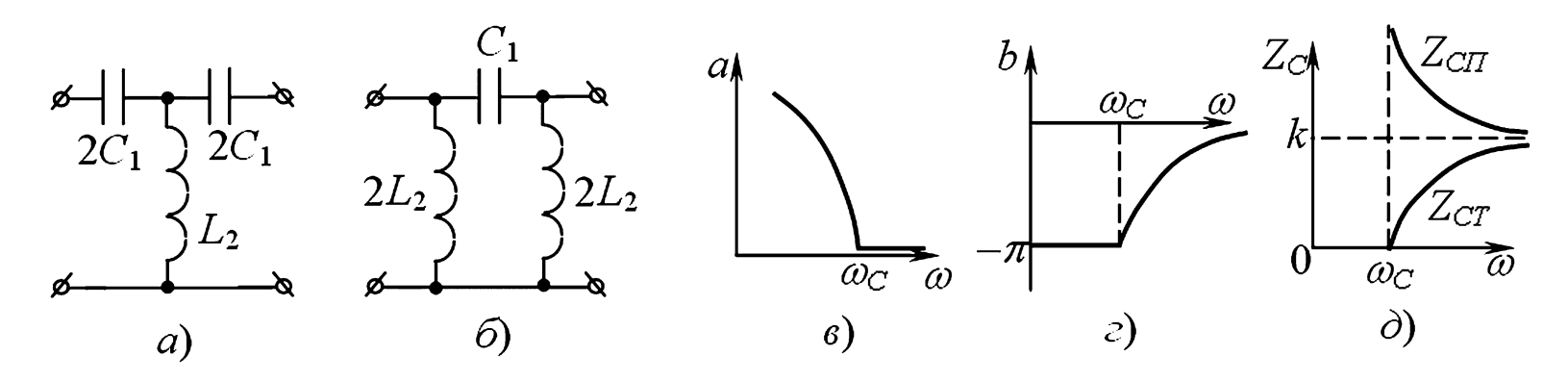
Рис. 4. Схемы высокочастотных фильтров типа k: а — Т-образная; б — П-образная; и зависимости от частоты: в — коэффициента затухания; г — коэффициента фазы; д — характеристического сопротивления.

1.3. Фильтры типа m

Фильтры типа k имеют два существенных недостатка:

Коэффициент затухания $a$ медленно нарастает вблизи частоты среза $\omega_c$.
Характеристическое сопротивление $Z_c$ сильно изменяется в зоне прозрачности, что мешает хорошему согласованию с нагрузкой.

Для устранения этих недостатков используют фильтры типа m (производные). Их получают из фильтров типа k, добавляя реактивное сопротивление противоположного знака в продольную или поперечную ветвь (Рис. 5а). Это создает LC-резонанс (параллельный или последовательный) в зоне затухания, на частоте $\omega_\infty$.

На этой частоте резонанса сопротивление одной из ветвей становится бесконечным (в Т-схеме) или нулевым (в П-схеме), что приводит к бесконечному затуханию ($a \to \infty$).

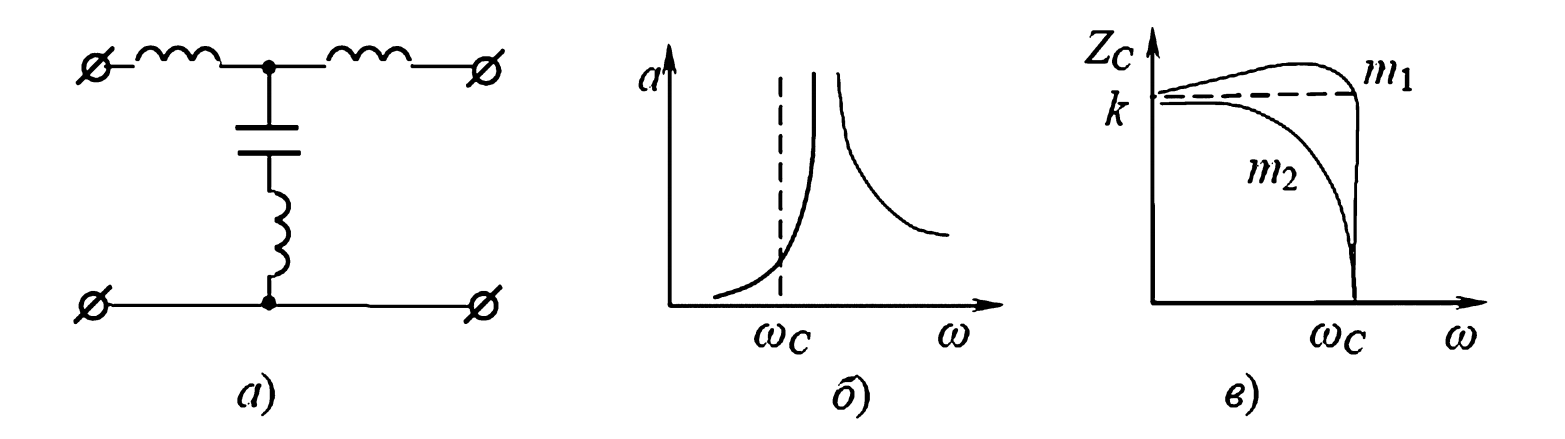
Рис. 5. Низкочастотный фильтр типа m: а — схема; зависимости от частоты: б — коэффициента затухания; в — характеристического сопротивления.

Как видно из графика (Рис. 5б), затухание очень резко возрастает сразу за частотой среза, достигая пика. Однако, при дальнейшем удалении от $\omega_c$, затухание начинает уменьшаться.

Параметр $m$ ( $0 < m < 1$ ) определяет, как близко к $\omega_c$ находится этот пик затухания. При $m \to 0$ пик уходит на бесконечность (превращаясь в k-фильтр).
Важнейшим преимуществом m-фильтров является их характеристическое сопротивление (Рис. 5в). При $m \approx 0.6$, $Z_c$ остается почти постоянным в 80-90% зоны прозрачности, что обеспечивает отличное согласование. На практике часто создают комбинированные фильтры: внутренние звенья делают типа k (для обеспечения затухания), а крайние звенья — типа m (для согласования с нагрузкой).

2. Активные фильтры

Пассивные LC-фильтры, особенно на низких частотах (аудио, телеметрия), требуют использования катушек индуктивности. Индуктивности — это громоздкие, дорогие, неидеальные (имеют активное сопротивление) компоненты, подверженные влиянию магнитных полей. Активные RC-фильтры решают эту проблему, полностью исключая индуктивности.

Они строятся на базе активных усилительных элементов (обычно операционных усилителей — ОУ) и пассивных RC-цепей. Существует множество схем таких фильтров.

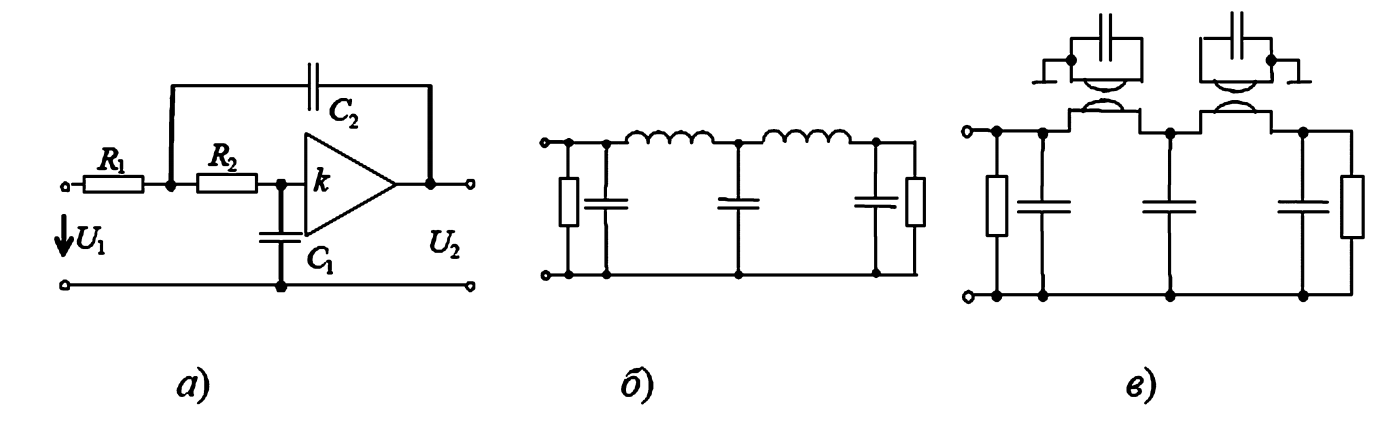
Рис. 6. Схемы фильтров: а — активный RC-фильтр; б — пассивный LC-фильтр (прототип); в — фильтр с имитацией индуктивности (на гираторах).

На Рисунке 6а приведена схема простейшего активного ФНЧ (например, фильтр Саллена-Ки). Его характеристики (крутизна спада, стабильность) сильно зависят от параметров ОУ и номиналов RC-цепей.

Более стабильный подход — имитация индуктивности. Пассивные LC-фильтры (Рис. 6б) обладают низкой чувствительностью к изменению номиналов элементов. С помощью специальных схем на ОУ, называемых гираторами, можно «превратить» конденсатор в эквивалентную индуктивность. Гиратор — это четырехполюсник, который «переворачивает» импеданс. Если к выходу гиратора подключить конденсатор $C$, то со входа схема будет выглядеть как индуктивность $L_{экв}$.

Это позволяет взять проверенную схему пассивного LC-прототипа (Рис. 6б) и заменить в ней все «плавающие» (незаземленные) индуктивности на связку «гиратор + конденсатор» (Рис. 6в). Такой подход позволяет получить активный фильтр с высокой стабильностью и предсказуемыми характеристиками пассивного прототипа, но без его недостатков (размеров и неидеальности катушек).

3. Сравнительная характеристика типов фильтров

Сведем ключевые особенности рассмотренных типов фильтров в единую таблицу для удобства сравнения.

Параметр	Фильтры типа k (пассивные)	Фильтры типа m (пассивные)	Активные RC-фильтры
Элементная база	Индуктивности (L) и конденсаторы (C)	Индуктивности (L) и конденсаторы (C)	Резисторы (R), конденсаторы (C) и активные элементы (ОУ)
Крутизна спада АЧХ	Низкая, плавная вблизи $\omega_c$	Высокая, с пиком затухания на $\omega_\infty$	Высокая, определяется порядком фильтра (количеством каскадов)
Стабильность $Z_c$	Низкая (сильно меняется в зоне прозрачности)	Высокая (при $m \approx 0.6$, $Z_c$ почти постоянно)	Высокое входное и низкое выходное R, легко согласуется
Размеры (на НЧ)	Большие (из-за L)	Большие (из-за L)	Компактные (нет индуктивностей)
Потребление энергии	Нет (пассивные)	Нет (пассивные)	Да (требует источник питания для ОУ)
Усиление сигнала	Невозможно (только затухание)	Невозможно (только затухание)	Возможно (может одновременно фильтровать и усиливать)
Основное применение	Простые ВЧ-приложения, звенья комбинированных фильтров	Входные/выходные звенья для согласования, ВЧ-приложения	Низкочастотная обработка сигналов (аудио, управление, медицина)

4. Интересные факты о фильтрах

Происхождение «k»: Название «фильтр типа k» происходит от «constant-k» (постоянная k). Это связано с тем, что в их конструкции произведение продольного ($Z_1$) и поперечного ($Z_2$) импедансов является константой ($Z_1 \cdot Z_2 = k^2$), не зависящей от частоты ($k^2 = L/C$).
Эволюция от k к m: Фильтры типа m (m-derived) были разработаны Отто Зобелем в 1920-х годах как прямое улучшение фильтров типа k, созданных Джорджем Кэмпбеллом. Основной задачей было решение проблемы плохого согласования импеданса.
«Магия» гиратора: Активная схема «гиратор», используемая для имитации индуктивности, получила свое название по аналогии с «трансформатором». Она выполняет «гирацию» — преобразование, которое «переворачивает» импеданс. Подключенный к гиратору конденсатор ($Z = 1/(j\omega C)$) со входа выглядит как индуктивность ($Z \sim j\omega L$).
Низкочастотная проблема: Главным стимулом к развитию активных RC-фильтров в 1960-70-х годах стала «низкочастотная проблема». Для фильтрации, например, звуковых частот ($< 20 \text{ кГц}$) требуются катушки индуктивности с огромными номиналами (десятки Генри), которые практически невозможно изготовить в компактном, качественном и дешевом виде.
Цифровое настоящее: Сегодня подавляющее большинство сложных задач фильтрации в телекоммуникациях, аудио и видео решается методами цифровой обработки сигналов (DSP). Аналоговый сигнал оцифровывается (АЦП), «фильтруется» с помощью математических алгоритмов в процессоре, а затем преобразуется обратно (ЦАП). Однако пассивные и активные фильтры по-прежнему незаменимы для защиты от помех, сглаживания (anti-aliasing) перед АЦП и в силовой электронике.

5. Часто задаваемые вопросы (FAQ)

1. Что такое частота среза?

Ответ: Это граничная частота ($\omega_c$), которая отделяет зону прозрачности (где сигнал проходит) от зоны затухания (где сигнал подавляется). В теории идеальных реактивных фильтров на этой частоте происходит резкий переход от $a=0$ к $a>0$.

2. Почему в реактивных фильтрах Z1 и Z2 должны быть разного типа (L и C)?

Ответ: Потому что условие для существования зоны прозрачности — $-2 \le Z_1 / (2Z_2) \le 0$. Отношение $Z_1/Z_2$ должно быть отрицательным вещественным числом. Если $Z_1 = j\omega L$ (положительное мнимое), а $Z_2 = 1/(j\omega C) = -j/(\omega C)$ (отрицательное мнимое), их отношение $(j\omega L) / (-j/(\omega C)) = -\omega^2 LC$, что является отрицательным и вещественным. Если бы они были одного типа (например, два индуктора), их отношение было бы положительным.

3. Какое главное преимущество m-фильтра над k-фильтром?

Ответ: У m-фильтра два главных преимущества: 1) Он имеет гораздо более резкий спад затухания сразу за частотой среза, так как у него есть «пик» бесконечного затухания. 2) При правильном выборе параметра $m \approx 0.6$ его характеристическое сопротивление $Z_c$ почти постоянно в зоне прозрачности, что позволяет идеально согласовать его с нагрузкой.

4. Почему в активных фильтрах не используют катушки индуктивности?

Ответ: Вся суть активных фильтров — избавиться от катушек индуктивности, особенно на низких частотах. Индуктивности громоздки, дороги, имеют большое внутреннее сопротивление (неидеальны), чувствительны к электромагнитным помехам и их сложно интегрировать в микросхемы. Активные фильтры заменяют их компактными, дешевыми и стабильными RC-цепями и операционными усилителями.

5. Что такое «зона прозрачности»?

Ответ: Это диапазон частот, в котором идеальный фильтр пропускает сигнал без ослабления (без затухания). В теории цепей это означает, что в этом диапазоне коэффициент затухания четырехполюсника $a = 0$.

Заключение

Частотные фильтры являются фундаментальными блоками в электротехнике, радиотехнике и обработке сигналов. Рассмотренная теория пассивных реактивных фильтров (типа k и m) заложила основу для проектирования цепей частотной селекции.

Фильтры типа k представляют собой базовую реализацию, в то время как фильтры типа m являются их усовершенствованием, предлагая более резкое затухание и превосходное согласование импеданса. С развитием микроэлектроники широчайшее распространение получили активные RC-фильтры, которые исключили необходимость в громоздких индуктивностях, особенно в низкочастотных приложениях, и добавили возможность усиления сигнала. Выбор между пассивными LC-фильтрами (которые до сихP пор доминируют в ВЧ-силовой электронике и радиопередатчиках) и активными RC-фильтрами (доминирующими в обработке сигналов) диктуется конкретной задачей, диапазоном частот и требованиями к мощности.

Нормативные документы

ГОСТ Р 70024.2-2022 — «Государственная система обеспечения единства измерений. Фильтры полосовые октавные и на долю октавы. Часть 2. Испытания в целях утверждения типа».

Электрические частотные фильтры: Теория, типы и анализ