Электрическая емкость конденсатора: Расчет, формулы, примеры

Содержание страницы

Емкость уединенного проводника
Емкость системы проводников и конденсаторы
Пример расчета емкости и энергии
Факторы, влияющие на емкость, и практические конструкции
Сравнение типов диэлектриков для конденсаторов
Область применения понятия «емкость»
Интересные факты о емкости
Часто задаваемые вопросы (FAQ)
Заключение

Электрическая емкость — это фундаментальная физическая характеристика, которая определяет способность проводника или системы проводников накапливать электрический заряд. По сути, она показывает, какой величины заряд необходимо сообщить телу, чтобы его электрический потенциал изменился на единицу.

Понятие емкости было введено в науку в XVIII веке, во времена активного изучения электричества. Эксперименты с «лейденской банкой» — первым в истории конденсатором, созданным в 1745 году, — наглядно продемонстрировали, что различные устройства могут «хранить» электричество. Это привело к необходимости количественной оценки данной способности, что и послужило толчком к формализации концепции электрической емкости.

Емкость уединенного проводника

Рассмотрим уединенное проводящее тело (например, металлический шар), которому сообщен заряд \(Q\). Этот заряд создает вокруг тела электрическое поле, и само тело приобретает потенциал \(U\) (по отношению к условному нулю, например, бесконечно удаленной точке). Опытным путем установлено, что для уединенного проводника его потенциал прямо пропорционален накопленному на нем заряду.

Электрической емкостью \(C\) уединенного проводящего тела называется скалярная физическая величина, равная отношению заряда \(Q\) этого тела к его потенциалу \(U\):

\(C = Q / U\) (1)

Таким образом, емкость характеризует способность тела накапливать электрический заряд. Чем больше емкость, тем больший заряд тело может накопить при заданном потенциале (или, наоборот, тем меньшее изменение потенциала вызовет сообщение телу определенного заряда).

Единицы измерения: В Международной системе единиц (СИ) емкость измеряется в Фарадах (Ф), в честь английского физика Майкла Фарадея. 1 Фарад — это очень большая величина: емкостью 1 Ф обладал бы уединенный шар радиусом около 9 миллионов километров.
\(1 \Phi = 1 \text{Кл} / 1 \text{В}\).
На практике применяются дольные единицы:

Микрофарад (мкФ): \(1 \text{ мкФ} = 1 \times 10^{-6} \text{ Ф}\)
Нанофарад (нФ): \(1 \text{ нФ} = 1 \times 10^{-9} \text{ Ф}\)
Пикофарад (пФ): \(1 \text{ пФ} = 1 \times 10^{-12} \text{ Ф}\)

Емкость системы проводников и конденсаторы

Понятие емкости также применимо к системе из двух уединенных проводников. Классическим примером является система, где заряды проводников равны по значению, но противоположны по знаку: \(Q_1 = Q\) и \(Q_2 = -Q\) (где \(Q > 0\)). В этом случае под емкостью системы понимают отношение заряда \(Q\) к разности потенциалов (напряжению) \(U_{12} = U\) между этими проводниками.

\(C = Q / U\)

Примером такой системы могут служить два параллельных провода линии электропередачи. Однако наиболее важным устройством, специально предназначенным для использования его электрической емкости, является электрический конденсатор.

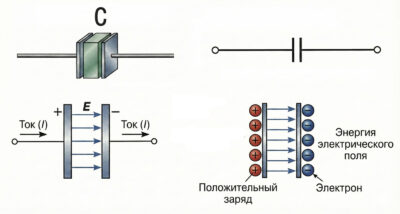
Конденсатор — это, по сути, система из двух проводников (называемых обкладками), разделенных слоем диэлектрика. На рисунке 1 изображена схема простейшего плоского конденсатора.

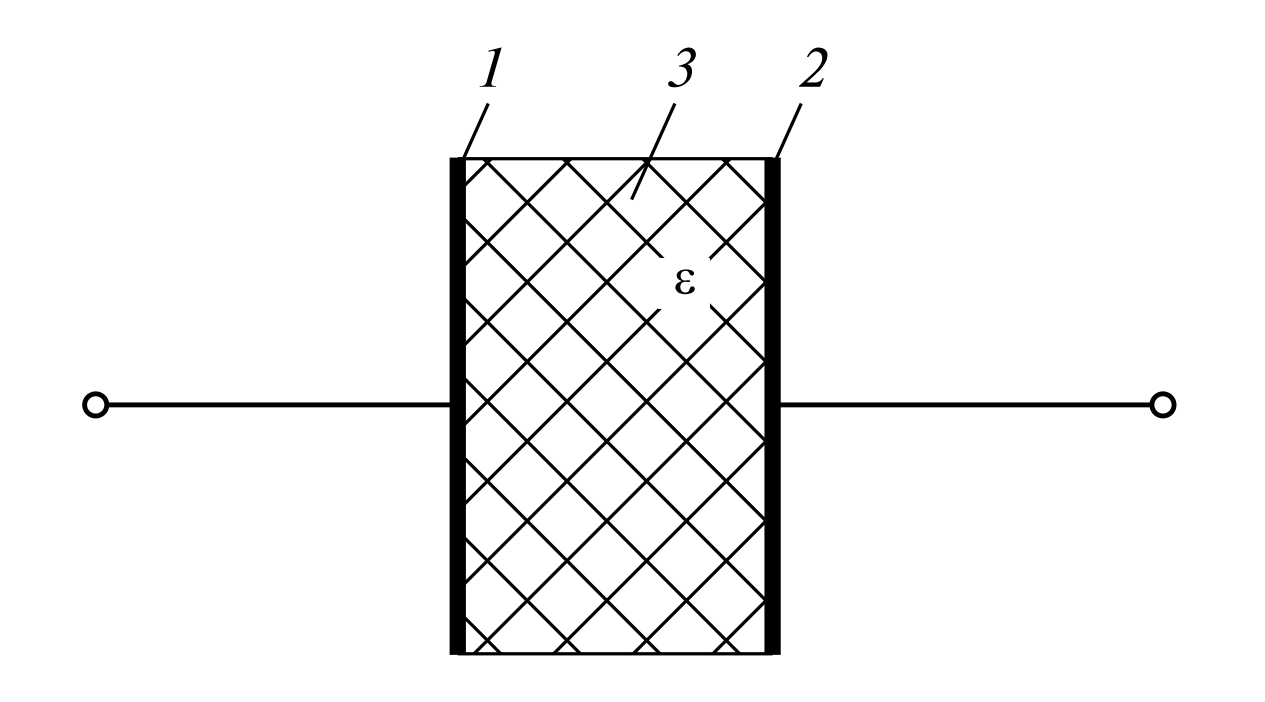
Рисунок 1. Схема устройства плоского конденсатора.
(1) – первая металлическая пластина (обкладка);
(2) – вторая металлическая пластина (обкладка);
(3) – слой диэлектрика между пластинами; (ε) – диэлектрическая проницаемость материала.

Как видно на рисунке 1, плоский конденсатор состоит из двух параллельных металлических пластин (обкладок) 1 и 2, которые разделены слоем диэлектрика 3. Емкость такого устройства также определяется выражением \(C = Q / U\), где \(Q\) — модуль заряда на одной из обкладок, а \(U\) — напряжение между ними.

Энергия электрического поля конденсатора

Основная функция конденсатора — накопление не только заряда, но и энергии электрического поля, сосредоточенного в диэстрике между обкладками. Эта запасенная энергия \(W_э\) рассчитывается по формулам:

\(W_э = \frac{Q \cdot U}{2} = \frac{C \cdot U^2}{2} = \frac{Q^2}{2C}\) (2)

Из формулы (2) следует, что при заданном напряжении \(U\) запасенная энергия будет тем больше, чем выше емкость \(C\) конденсатора.

Емкость плоского конденсатора

В первом приближении, когда можно пренебречь краевыми эффектами (неоднородностью поля у краев пластин), емкость плоского конденсатора можно рассчитать по следующей формуле:

\(C = \frac{\varepsilon \cdot s}{l}\) (3)

Где:

\(C\) — емкость конденсатора (Ф);
\(s\) — площадь каждой из металлических пластин (обкладок) (м²);
\(l\) — расстояние между пластинами (толщина диэлектрика) (м);
\(\varepsilon\) — диэлектрическая проницаемость диэлектрика, размещенного между пластинами (Ф/м). Эта величина характеризует электрофизические свойства вещества диэлектрика.

Диэлектрическая проницаемость \(\varepsilon\) часто представляется в виде \(\varepsilon = \varepsilon_0 \cdot \varepsilon_r\), где \(\varepsilon_0\) — электрическая постоянная (диэлектрическая проницаемость вакуума), а \(\varepsilon_r\) — относительная диэлектрическая проницаемость среды (безразмерная величина, показывающая, во сколько раз емкость конденсатора с данным диэлектриком больше, чем с вакуумом).

Электрическая постоянная (\(\varepsilon_0\)):
\( \varepsilon_0 \approx 8,85 \times 10^{-12} \text{ Ф/м} \)

Для воздушного конденсатора (у которого \(\varepsilon_r \approx 1\), и \(\varepsilon \approx \varepsilon_0\)), зависимость емкости \(C\) от отношения площади к расстоянию \(s/l\) представлена в таблице 1.

Таблица 1. Зависимость емкости воздушного конденсатора от \(s/l\)

Отношение \(s/l\), мм	1	2	5	10	20	50	100
Емкость \(C\), пФ	8,86	17,7	44,3	88,6	177	443	886

Пример расчета емкости и энергии

Задача: Плоский конденсатор имеет пластины площадью \(s = 100 \text{ см}^2 = 1 \times 10^{-2} \text{ м}^2\). Расстояние между ними \(l = 5 \text{ мм} = 5 \times 10^{-3} \text{ м}\). Пространство между пластинами заполнено диэлектриком с диэлектрической проницаемостью \(\varepsilon = 2,5 \times 10^{-10} \text{ Ф/м}\). Необходимо определить емкость конденсатора и энергию, запасенную в его поле, если напряжение между пластинами \(U = 4000 \text{ В}\).

Решение:

1. Определим емкость конденсатора, используя формулу (3):

\(C = \frac{\varepsilon \cdot s}{l} = \frac{(2,5 \times 10^{-10} \text{ Ф/м}) \cdot (1 \times 10^{-2} \text{ м}^2)}{5 \times 10^{-3} \text{ м}} = 0,5 \times 10^{-9} \text{ Ф} = 500 \text{ пФ}\)

2. Рассчитаем запасенную энергию по формуле (2):

\(W_э = \frac{C \cdot U^2}{2} = \frac{(0,5 \times 10^{-9} \text{ Ф}) \cdot (4000 \text{ В})^2}{2} = \frac{(0,5 \times 10^{-9}) \cdot (16 \times 10^6)}{2} = 4 \times 10^{-3} \text{ Дж} = 4 \text{ мДж}\)

Ответ: Емкость конденсатора составляет 500 пФ, а запасенная энергия — 4 мДж.

Факторы, влияющие на емкость, и практические конструкции

Как следует из формулы (3), для достижения большей емкости плоского конденсатора при использовании заданного диэлектрика, необходимо:

Увеличивать площадь пластин (\(s\)).
Уменьшать расстояние между ними (\(l\)).

Однако оба эти пути имеют физические и конструктивные ограничения:

Пробой диэлектрика: Чрезмерное сближение пластин (уменьшение \(l\)) недопустимо. Каждому диэлектрику свойственна определенная электрическая прочность — напряженность поля, при которой происходит пробой (разрушение диэлектрика и возникновение разряда). При уменьшении \(l\) напряженность поля (\(E \approx U/l\)) растет, что увеличивает риск пробоя.
Габариты: Размеры пластин (\(s\)) также не могут быть слишком большими из-за неизбежной громоздкости и увеличения стоимости такого конденсатора.

Поэтому в современной электротехнике и электронике для достижения больших значений емкости при относительно малых габаритах используются иные, более сложные конструкции конденсаторов (например, рулонные, многослойные керамические, электролитические), которые позволяют максимально увеличить эффективную площадь поверхности обкладок.

Сравнение типов диэлектриков для конденсаторов

Выбор диэлектрика (материала «3» на рис. 1) является ключевым фактором, определяющим характеристики конденсатора.

Тип диэлектрика	Относительная проницаемость (\(\varepsilon_r\))	Преимущества	Недостатки
Воздух / Вакуум	~1	Высокая стабильность, низкие потери, высокая электрическая прочность.	Очень низкая емкость на единицу объема.
Полимерная пленка (ПЭТ, полипропилен)	2 — 3.5	Хорошая стабильность, низкие утечки, высокая надежность.	Средняя емкость, чувствительность к температуре.
Керамика (Тип 1, NP0/C0G)	15 — 100	Высочайшая стабильность (температурная, временная), низкие потери.	Относительно низкая емкость.
Керамика (Тип 2, X7R, Y5V)	300 — 10 000+	Очень высокая емкость на единицу объема.	Низкая стабильность (зависимость от T и U), высокие потери, старение.
Оксидная пленка (Электролитические)	7 — 30 (для Al₂O₃)	Огромная емкость при малых размерах.	Полярность (нельзя путать +/-), высокие утечки, ограниченный срок службы.

Область применения понятия «емкость»

В заключение необходимо отметить, что емкостью обладают не только специально созданные устройства (конденсаторы), проводники или пары проводников. Емкость — это свойство, присущее любым проводящим телам и их системам в пространстве.

Ее особенно необходимо учитывать (как полезный или, наоборот, паразитный эффект), если тела в системе отличаются большой площадью взаимной поверхности и расположены близко одно к другому. Емкости подобных «случайных» систем тел (например, дорожек на печатной плате, витков катушки индуктивности или жил в кабеле) могут достигать значительных величин и аккумулировать большие энергии электрических полей, влияя на работу всего устройства.

Интересные факты о емкости

Емкость Земли: Емкость уединенного проводника в виде шара равна \(C = 4\pi\varepsilon_0 R\). Если принять радиус Земли \(R \approx 6400 \text{ км}\), ее расчетная емкость составит всего около 710 микрофарад (мкФ).
Суперконденсаторы (Ионисторы): Современные технологии позволяют создавать компоненты с гигантской емкостью — ионисторы. Их емкость достигает тысяч Фарад! Это достигается за счет использования двойного электрического слоя на границе электрода и электролита, где «расстояние» \(l\) измеряется ангстремами (размерами молекул).
«Лейденская банка»: Первый конденсатор был изобретен случайно в 1745 году. Он представлял собой стеклянную банку, наполненную водой (внутренняя обкладка), которую держали в руке (внешняя обкладка). Стекло служило диэлектриком.
Емкость человека: Тело человека также обладает электрической емкостью. Стоя на полу, человек образует конденсатор с «землей», и емкость этой системы составляет порядка 100-200 пикофарад (пФ).
Паразитная емкость: В высокочастотной электронике инженерам приходится бороться с «паразитной» емкостью — нежелательной емкостью, возникающей между любыми двумя проводниками (например, выводами транзистора или дорожками на плате). Эта емкость может приводить к сбоям в работе схем.

Часто задаваемые вопросы (FAQ)

1. Что произойдет, если превысить напряжение, указанное на конденсаторе?

2. Почему электролитические конденсаторы имеют полярность (+ и -)?

3. Как соединяются конденсаторы в батареи?

4. Что такое «относительная диэлектрическая проницаемость» (\(\varepsilon_r\))?

5. От чего, кроме геометрии, зависит емкость?

Заключение

Электрическая емкость является одной из трех ключевых пассивных характеристик электрических цепей, наряду с сопротивлением и индуктивностью. Она описывает способность системы накапливать электрический заряд и энергию электрического поля. Это свойство лежит в основе работы конденсаторов — незаменимых компонентов в фильтрах, колебательных контурах, блоках питания и схемах памяти.

Понимание факторов, от которых зависит емкость — геометрических размеров (площади пластин, расстояния между ними) и физических свойств диэлектрика, — позволяет инженерам проектировать устройства с заданными характеристиками для решения широкого круга технических задач.

Нормативная база

Классификация, параметры и методы испытаний конденсаторов в Российской Федерации и странах СНГ регламентируются системой стандартов ГОСТ. Ключевые из них:

ГОСТ IEC 60384-1-2003 — Конденсаторы постоянной емкости для электронной аппаратуры. Часть 1. Общие технические условия.

Список литературы

Калашников, А. Г. Электричество. – М.: Физматлит, 2003. – 624 с.
Бессонов, Л. А. Теоретические основы электротехники: Электрические цепи. – 11-е изд. – М.: Гардарики, 2007. – 701 с.
Иродов, И. Е. Электромагнетизм. Основные законы. – 5-е изд., испр. – М.: БИНОМ. Лаборатория знаний, 2009. – 319 с.
Зевеке, Г. В., Ионкин, П. А., Нетушил, А. В., Страхов, С. В. Основы теории цепей. – М.: Энергоатомиздат, 1989. – 528 с.