Диэлектрические потери: теория, физика процессов, расчет

Содержание страницы

1. Физическая природа диэлектрических потерь
2. Схемы замещения диэлектрика: Математическое моделирование
3. Аналитический вывод формул расчета мощности потерь
4. Анализ факторов, влияющих на диэлектрические потери
5. Влияние внешних факторов: Частота и Температура
6. Практическое применение: Диагностика и Тепловой пробой
7. Интересные факты о диэлектрических потерях
8. FAQ: Часто задаваемые вопросы
Заключение

Диэлектрические потери — это часть энергии электрического поля, которая необратимо рассеивается в изоляционном материале (диэлектрике), преобразуясь в тепло. Это фундаментальное паразитное явление в электротехнике, определяющее качество изоляции, срок службы оборудования и предельные параметры линий электропередач. Простыми словами, это та цена, которую мы платим природе за несовершенство материалов при работе с электричеством.

Представьте, что вы толкаете тяжелую тележку (электрическое поле) через густую траву (диэлектрик). Даже если вы не совершаете полезной работы (не везете груз в гору), вам все равно приходится тратить силы на преодоление сопротивления травы, приминая её. Эта потраченная впустую энергия, уходящая на «нагрев» травы и вашу усталость, и есть аналог диэлектрических потерь. В идеальном вакууме (на асфальте) потерь бы почти не было.

Краткая история. Интерес к диэлектрическим потерям возник в конце XIX века с началом эры переменного тока. Когда Майкл Фарадей исследовал диэлектрики, он заметил, что разные материалы ведут себя по-разному в электрическом поле. Однако настоящая проблема возникла, когда Себастьян Ферранти прокладывал первые высоковольтные кабели в Лондоне в 1890-х годах. Инженеры заметили, что кабели греются даже без нагрузки. Теоретическую базу подвел Джеймс Клерк Максвелл, а позже Петер Дебай в начале XX века разработал теорию дипольной релаксации, объяснившую природу потерь на молекулярном уровне. С тех пор борьба за снижение «тангенса дельта» стала главной задачей материаловедов.

1. Физическая природа диэлектрических потерь

Чтобы понять, откуда берутся потери, необходимо заглянуть внутрь вещества. Диэлектрик не является абсолютным изолятором. В нем протекают сложные физико-химические процессы при наложении поля. Потери мощности \( P_{\text{д}} \) обусловлены двумя основными факторами: током сквозной проводимости и током абсорбции (поляризации).

1.1. Виды поляризации и механизмы потерь

В переменном электрическом поле заряженные частицы внутри материала начинают колебаться. Это движение не происходит мгновенно и без трения.

Потери на электропроводность (Сквозной ток): Даже в лучшем диэлектрике есть свободные носители заряда (ионы, электроны). Они движутся сквозь толщу материала, создавая реальный ток утечки, подчиняющийся закону Джоуля-Ленца. Это характерно для стекол и керамики при высоких температурах.
Релаксационные потери: Связаны с поворотом полярных молекул (диполей). Диполь пытается повернуться вслед за полем, но «вязкость» вещества мешает ему. Трение молекул друг о друга вызывает нагрев. Это основной вид потерь в жидких диэлектриках и полимерах.
Ионизационные потери: Возникают в газовых включениях внутри твердой изоляции. Если напряженность поля высока, газ ионизируется (возникает тихий разряд), что ведет к разогреву и разрушению окружающего материала.

Важно понимать: ионизационные потери являются самыми опасными для высоковольтной изоляции. Они приводят к появлению частичных разрядов (ЧР), которые, подобно червям, прогрызают изоляцию изнутри, создавая проводящие каналы — дендриты.

2. Схемы замещения диэлектрика: Математическое моделирование

Для инженерных расчетов и анализа состояния изоляции реальный физический объект (конденсатор, кабель, изолятор) заменяют идеализированной электрической схемой. Существуют две классические упрощенные схемы замещения: параллельная и последовательная. Они позволяют свести сложные физические процессы к понятным элементам цепи: идеальному конденсатору (емкость) и активному резистору (потери).

Основной характеристикой, определяющей качество диэлектрика, является тангенс угла диэлектрических потерь \( \text{tg}\delta \).

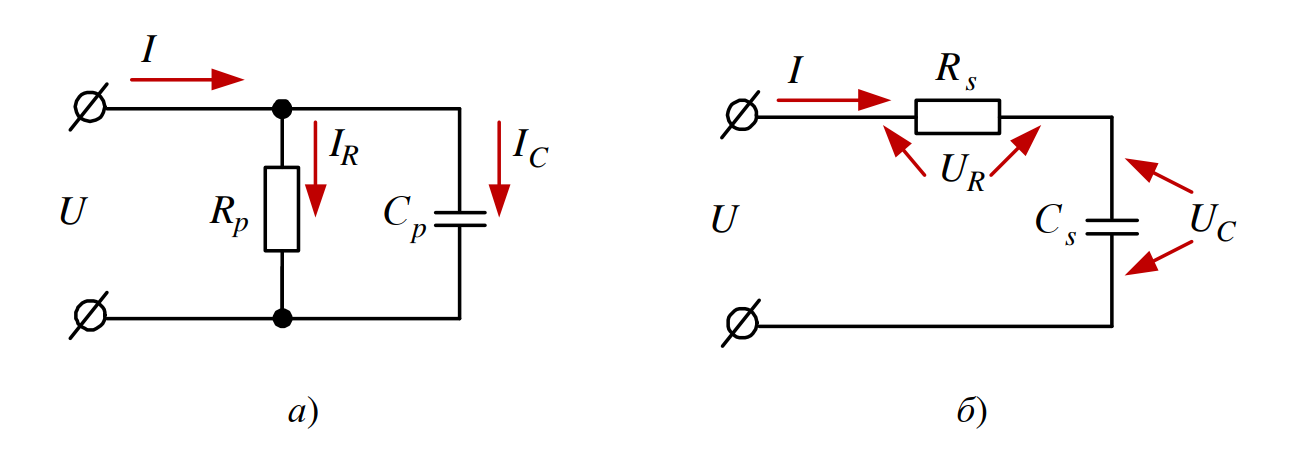
Рис. 1. Упрощенные схемы замещения диэлектрика: а — параллельная; б — последовательная.
Обозначения: \( U \) — напряжение, подаваемое на диэлектрик; \( I \) — общий эквивалентный ток утечки;
\( R_p \) и \( C_p \) — эквивалентные сопротивление и емкость в параллельной схеме;
\( I_R \) — активная (греющая) составляющая тока \( I \);
\( I_C \) — емкостная (реактивная) составляющая тока \( I \);
\( R_s \) и \( C_s \) — эквивалентные сопротивление и емкость в последовательной схеме;
\( U_R \) — активная составляющая падения напряжения;
\( U_C \) — емкостная составляющая падения напряжения.

Разберем детально каждую схему.

Параллельная схема (рис. 1, а): Она наиболее точно описывает физические процессы в большинстве технических диэлектриков при низких частотах и высоких напряжениях. Здесь ток \( I \) разделяется на два потока: емкостный \( I_C \) (зарядка емкости) и активный \( I_R \) (утечка и потери).
Последовательная схема (рис. 1, б): Удобна для описания процессов при высоких частотах или когда потери в диэлектрике очень велики. Здесь общее напряжение \( U \) делится на падение напряжения на емкости \( U_C \) и на активном сопротивлении \( U_R \).

Векторные диаграммы

Для визуализации фазовых соотношений между токами и напряжениями используются векторные диаграммы. Они позволяют наглядно увидеть, что такое «угол потерь».

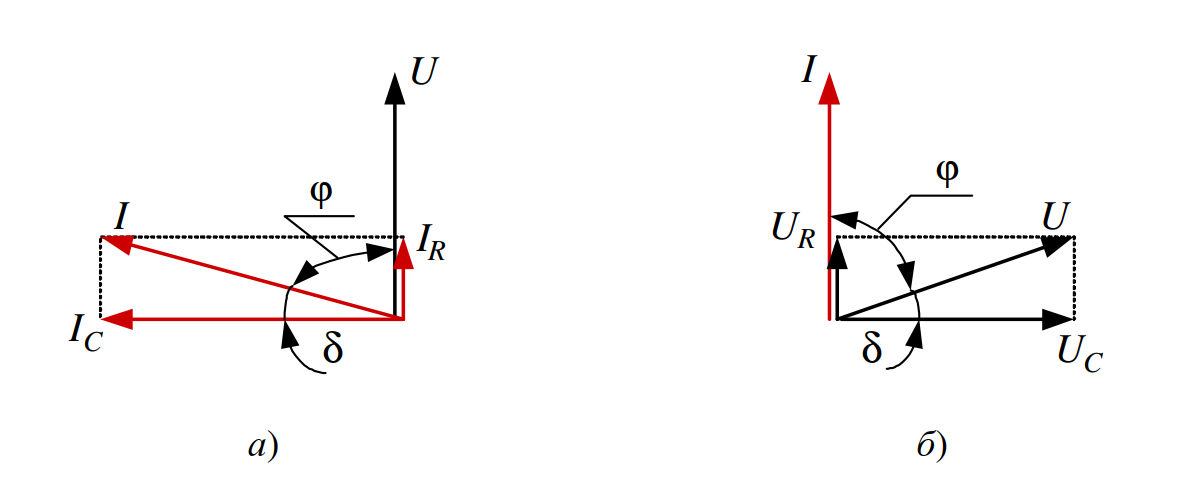
Рис. 2. Векторные диаграммы для схем замещения диэлектрика: а — параллельной; б — последовательной.
\( \delta \) — угол диэлектрических потерь; \( \phi \) — фазовый сдвиг между током и напряжением.

Угол \( \delta \) на рис. 2 называется углом диэлектрических потерь. Физический смысл этого угла чрезвычайно важен: он дополняет до 90° фазовый сдвиг \( \phi \) между током и напряжением в цепи реального диэлектрика.

В идеальном диэлектрике (без потерь) ток опережает напряжение ровно на 90°, то есть \( \phi = 90^\circ \), а \( \delta = 0^\circ \).
Чем хуже изоляция, тем больше активный ток, тем больше угол \( \delta \) и меньше угол \( \phi \).

3. Аналитический вывод формул расчета мощности потерь

Проведем строгий математический вывод формул, связывающих измеряемые параметры с мощностью, которая идет на нагрев изоляции.

3.1. Расчет для параллельной схемы замещения

Рассмотрим параллельную схему (рис. 1, а). Мощность потерь — это активная мощность, выделяемая на резисторе \( R_p \).

P_{\text{д}} = U \cdot I_R = \frac{U^2}{R_p} \quad (1)

Из векторной диаграммы (рис. 2, а) видно, что отношение активного тока к емкостному равно тангенсу угла потерь:

\text{tg}\delta = \frac{I_R}{I_C} \Rightarrow I_R = I_C \cdot \text{tg}\delta \quad (2)

Согласно теории цепей переменного тока, емкостный ток определяется через реактивное сопротивление \( X_C \):

X_C = \frac{1}{\omega C_p} = \frac{1}{2\pi f C_p} \quad (3)

Где \( f \) — частота сети (Гц), а \( C_p \) — эквивалентная емкость параллельной схемы. Применяя закон Ома для емкостной ветви, получаем:

I_C = \frac{U}{X_C} = U \cdot 2\pi f C_p = U \omega C_p \quad (4)

Теперь соберем все вместе. Подставим (4) в (2), чтобы найти \( I_R \), а затем результат подставим в базовую формулу мощности (1). Получим фундаментальное уравнение диэлектрических потерь:

P_{\text{д}} = U \cdot (U \omega C_p \cdot \text{tg}\delta) = U^2 \omega C_p \text{tg}\delta = 2\pi f C_p U^2 \text{tg}\delta \quad (5)

Формула (5) является основной для расчетов в энергетике. Она показывает, что потери растут квадратично с ростом напряжения! Увеличение напряжения в 2 раза приведет к росту нагрева в 4 раза.

3.2. Расчет для последовательной схемы замещения

Для схемы на рис. 1, б, мощность потерь выделяется на сопротивлении \( R_s \):

P_{\text{д}} = I^2 R_s = U_R \cdot I \quad (6)

Из векторной диаграммы (рис. 2, б) следует соотношение напряжений:

\text{tg}\delta = \frac{U_R}{U_C} \quad (7)

Полное напряжение \( U \) связано с составляющими по теореме Пифагора (для векторов):

U = \sqrt{U_R^2 + U_C^2} \quad (8)

Ток \( I \) в последовательной цепи един и равен:

I = \frac{U_C}{X_C} = U_C \cdot 2\pi f C_s \quad (9)

Проведя ряд алгебраических преобразований (выразив \( U_C \) и \( U_R \) через \( U \) и \( \text{tg}\delta \)), мы получим выражение для последовательной схемы:

P_{\text{д}} = \frac{U^2 \omega C_s \text{tg}\delta}{1 + \text{tg}^2\delta} \quad (10)

3.3. Сравнение схем и практический вывод

Если изоляция качественная, то угол потерь очень мал. Математически это значит, что \( \text{tg}\delta < 0,1 \). В этом случае \( \text{tg}^2\delta \) становится пренебрежимо малой величиной (меньше 0,01), и знаменатель в формуле (10) стремится к единице.

Следовательно, при \( \text{tg}\delta < 0,1 \) формулы (5) и (10) становятся идентичными:

P_{\text{парал}} \approx P_{\text{послед}} \approx U^2 \omega C \text{tg}\delta

Именно поэтому на практике инженеры почти всегда используют параллельную схему замещения и формулу (5) как наиболее удобную.

4. Анализ факторов, влияющих на диэлектрические потери

Понимание того, от чего зависит \( \text{tg}\delta \), позволяет диагностировать состояние оборудования.

4.1. Влияние типа диэлектрика

Значения \( \text{tg}\delta \) варьируются на порядки для разных состояний вещества:

Газы: Самые лучшие изоляторы. При напряжениях ниже порога ионизации \( \text{tg}\delta \approx 10^{-8} \). Потери практически отсутствуют.
Жидкие диэлектрики (масла): \( \text{tg}\delta \) от \( 10^{-4} \) до \( 10^{-2} \). Сильно зависит от очистки масла.
Твердые диэлектрики:
- Неполярные (полиэтилен, фторопласт): \( 10^{-4} — 10^{-5} \).
- Полярные (бакелит, ПВХ): \( 10^{-2} — 10^{-3} \).

4.2. Влияние влажности

Вода — главный враг изоляции! Молекулы воды являются сильными диполями.

Попадание влаги в пористые диэлектрики (бумага, картон, текстолит) приводит к резкому росту \( \text{tg}\delta \). Например, для сухой кабельной бумаги \( \text{tg}\delta \approx 0,002 \), а при увлажнении он может вырасти до \( 0,35 \) и выше. Это увеличивает ток проводимости и потери на поляризацию. Именно поэтому мощные трансформаторы перед заливкой маслом сушат в вакуумных печах сутками.

4.3. Влияние напряжения и частоты

Напряжение: Как следует из формулы (5), \( P_{\text{д}} \sim U^2 \). В высоковольтных ЛЭП и установках (110 кВ, 220 кВ и выше) даже малый \( \text{tg}\delta \) приводит к значительным потерям энергии в киловаттах. Кроме того, при превышении критического напряжения начинается ионизация газовых пор, что вызывает лавинообразный рост \( \text{tg}\delta \) (кривая ионизации).
Частота: \( P_{\text{д}} \sim f \). В высокочастотной технике потери могут быть колоссальными. Пример применения: Микроволновая печь работает именно на принципе диэлектрических потерь. Высокочастотное поле (2.4 ГГц) заставляет молекулы воды в еде бешено вращаться, создавая трение и нагрев. Промышленный пример: Высокочастотная сушка древесины или обмоток электродвигателей, где тепло генерируется сразу внутри всего объема материала.

5. Влияние внешних факторов: Частота и Температура

Диэлектрические потери не являются статичной величиной. Они динамически изменяются в зависимости от условий эксплуатации оборудования. В современной энергетике этот вопрос стоит особенно остро из-за массового внедрения силовой электроники.

5.1. Проблема высоких частот в современной энергетике

Классическая электротехника оперировала частотой 50 Гц. Однако современная промышленность широко использует частотные преобразователи (ПЧ) и инверторы для управления электродвигателями. Ключевые элементы этих устройств (IGBT-транзисторы) работают в режиме широтно-импульсной модуляции (ШИМ) с несущими частотами, достигающими 100 кГц и выше.

Появление высокочастотных гармоник напряжения приводит к колоссальному стрессу изоляции стандартных силовых кабелей. Поскольку потери \( P_{\text{д}} \) прямо пропорциональны частоте \( f \) (см. формулу 5), даже небольшое напряжение высокой частоты вызывает интенсивный локальный разогрев диэлектрика.

Обычный кабель из сшитого полиэтилена (XLPE), рассчитанный на 50 Гц, при работе с частотным приводом может разогреваться изнутри, даже если токовая нагрузка жилы находится в пределах нормы. Это явление называют «диэлектрическим нагревом», и оно часто становится причиной необъяснимых аварий на производстве.

5.2. Анализ зависимостей \(\text{tg}\delta\) (Рис. 3)

Для инженера критически важно понимать, как меняется тангенс угла потерь при изменении температуры диэлектрика \( \theta \) и частоты сети \( f \). Эти фундаментальные зависимости проиллюстрированы на графиках ниже.

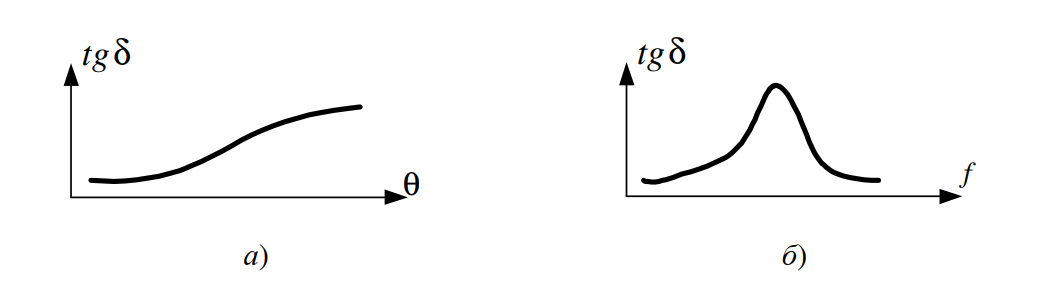
Рис. 3. Зависимости тангенса угла диэлектрических потерь: а — от температуры диэлектрика \( \theta \); б — от частоты напряжения \( f \).

а) Влияние температуры (Тепловые процессы)

Как видно из графика на рис. 3, а, с ростом температуры \( \theta \) наблюдается рост \( \text{tg}\delta \). Физика этого процесса заключается в следующем: нагрев вещества — это увеличение кинетической энергии его молекул. Интенсивные тепловые колебания решетки приводят к двум эффектам:

Ослабление связей: Электронам и ионам становится проще оторваться от своих атомов и стать свободными носителями заряда.
Снижение вязкости: В жидких и размягченных диэлектриках ионам легче перемещаться сквозь материал.

Оба фактора приводят к резкому возрастанию сквозного тока утечки (активной составляющей \( I_R \)), что неизбежно увеличивает потери. Если процесс не контролировать, может наступить тепловой пробой.

б) Влияние частоты (Релаксационная поляризация)

График на рис. 3, б имеет характерный «горб» (максимум). Это классическое проявление релаксационных потерь. Почему кривая ведет себя именно так?

Представьте переполненный автобус (диэлектрик), где пассажиры (диполи) пытаются перебежать от одной стены к другой по команде кондуктора (электрическое поле).

Низкая частота (команды раз в минуту): Пассажиры легко успевают перебежать и спокойно стоят. Трения почти нет. Потери малы.
Высокая частота (команды каждую секунду): Люди просто не успевают среагировать из-за своей инерции и давки. Они стоят на месте и лишь слегка дергаются. Движения нет — трения (нагрева) нет. Потери снова малы.
Средняя частота: Команды подаются именно в том темпе, когда люди успевают разогнаться, но тут же вынуждены тормозить и бежать обратно. Возникает максимальная суета, толкотня и нагрев. Это и есть максимум \( \text{tg}\delta \).

Научное объяснение таково:

На низких частотах: Процесс поляризации успевает полностью завершиться за половину периода напряжения. Диполи поворачиваются синхронно с полем. Токи абсорбции малы.
На высоких частотах: Из-за инерции молекул и внутренней вязкости вещества диполи просто «не успевают» следовать за быстрым изменением вектора поля. Поляризация практически отсутствует, а значит, нет и потерь энергии на трение диполей.
Область максимума: На средних частотах (куда часто попадает и промышленная частота 50 Гц для высоковольтных бумажно-масляных изоляций) период колебаний поля соизмерим со временем релаксации молекул. Сдвиг фаз между полем и движением частиц максимален, что и дает пик на графике потерь.

6. Практическое применение: Диагностика и Тепловой пробой

Тепловой пробой

Существует опасная положительная обратная связь.

При работе изоляция греется из-за потерь \( P_{\text{д}} \).
С ростом температуры у многих диэлектриков растет \( \text{tg}\delta \).
Рост \( \text{tg}\delta \) приводит к еще большему выделению тепла (см. формулу 5).
Температура растет еще сильнее.

Если теплоотвод хуже тепловыделения, происходит тепловой пробой — изоляция плавится, обугливается и теряет свои свойства, что приводит к короткому замыканию и взрыву.

Сравнительная таблица методов оценки изоляции

Параметр	Физический смысл	Тип тока измерения	Что выявляет
Сопротивление изоляции (\(R_{iso}\))	Способность препятствовать сквозному току	Постоянный (DC)	Грубые дефекты, сильное загрязнение, замыкание.
Коэффициент абсорбции (\(K_{abs}\))	Степень увлажнения (отношение R60/R15)	Постоянный (DC)	Увлажнение изоляции.
Тангенс угла потерь (\(\text{tg}\delta\))	Интегральная характеристика потерь энергии	Переменный (AC)	Общее старение, увлажнение всего объема, начало ионизации, наличие газовых включений.

Преимущества и недостатки измерения \(\text{tg}\delta\)

Преимущества:

Позволяет обнаружить дефекты, которые не видны при замере сопротивления мегаомметром (например, диэлектрические потери в распределенных слоях).
Является безразмерной величиной, не зависящей от геометрических размеров изолятора (в отличие от сопротивления изоляции, которое падает с ростом площади).

Недостатки:

Требует сложного оборудования (мост Шеринга или цифровые измерители).
Измерения часто требуют подачи высокого напряжения, что требует строгих мер безопасности.
Результат является усредненным: локальный маленький дефект может быть «замаскирован» большим объемом хорошей изоляции.

7. Интересные факты о диэлектрических потерях

Кулинарная физика. Принцип работы микроволновой печи основан исключительно на диэлектрических потерях. Электромагнитные волны частотой 2,45 ГГц заставляют дипольные молекулы воды в пище вращаться с огромной скоростью, создавая трение и нагрев. Сухая тарелка остается холодной, так как в керамике (при этой частоте) tgδ очень мал.
Технология «Стелс». Покрытия военных самолетов-невидимок содержат специальные композитные материалы с высоким значением тангенса угла потерь в радиодиапазоне. Они не отражают волны радара, а поглощают их энергию, превращая её в ничтожное количество тепла, тем самым делая объект невидимым для локаторов.
Исторический парадокс. В 1890 году Себастьян Ферранти проложил первый высоковольтный кабель на 10 кВ в Лондоне. Инженеры были шокированы тем, что напряжение на конце длинной линии оказалось выше, чем в начале (эффект Ферранти), но еще больше их удивило, что кабель нагревался даже без подключенной нагрузки — так человечество впервые серьезно столкнулось с диэлектрическими потерями.
Медицинская польза. Явление, вредное в энергетике, спасает жизни в медицине. Метод УВЧ-терапии и диатермии использует диэлектрические потери для глубокого прогрева тканей организма человека, который, по сути, является диэлектриком с потерями.
Стекло-предатель. Обычное стекло при комнатной температуре — отличный изолятор. Однако с ростом температуры его диэлектрические потери растут лавинообразно. В расплавленном состоянии стекло становится проводником электрического тока, и его варят в печах, пропуская ток прямо через жидкую массу.
Электрические «черви». Высокий tgδ часто сигнализирует о начале образования дендритов — микроскопических каналов внутри пластиковой изоляции кабелей. Они ветвятся подобно корням деревьев или ходам червей, постепенно прогрызая путь для будущего пробоя.
Ледяная загадка. Вода в жидком виде имеет огромные диэлектрические потери (поэтому мокрая изоляция — это плохо). Однако, как только вода замерзает и превращается в лед, её диэлектрические потери на низких частотах резко падают, так как кристаллическая решетка жестко фиксирует молекулы, не давая им вращаться.

8. FAQ: Часто задаваемые вопросы

Почему tgδ измеряют именно на переменном токе?

Потому что на постоянном токе (DC) отсутствуют процессы поляризации, вызывающие основные потери в качественной изоляции. Постоянный ток позволяет оценить только сквозную проводимость (сопротивление изоляции R_iso), тогда как переменный ток выявляет потери на перемагничивание диполей и ионизацию газовых включений.

Можно ли измерить диэлектрические потери обычным мультиметром?

Нет, это невозможно. Обычный мультиметр работает на низком напряжении постоянного тока. Для измерения tgδ требуется специализированное оборудование (мост Шеринга или цифровые измерители типа «Вектор», «Тангенс»), которое подает на объект высокое переменное напряжение (обычно 10 кВ) для имитации реальных условий работы.

Что хуже: низкое сопротивление изоляции или высокий tgδ?

Это показатели разных дефектов. Низкое сопротивление указывает на грубое нарушение целостности, грязь или прямое замыкание. Высокий tgδ — более тонкий индикатор. Он может показать общее старение, увлажнение или наличие пустот в изоляции, которая по мегаомметру еще кажется «нормальной». Поэтому для высоковольтного оборудования критически важны оба параметра.

Зависит ли тангенс угла потерь от геометрических размеров изолятора?

В теории — нет. Тангенс угла потерь — это качественная характеристика материала, она не зависит от размеров (толщины, площади) изолятора, в отличие от сопротивления или емкости. Это делает tgδ универсальным параметром для сравнения состояния изоляции маленького ввода и огромного трансформатора.

Заключение

Диэлектрические потери и их основной индикатор — тангенс угла дельта (\(\text{tg}\delta\)) — являются важнейшими понятиями в современной электроэнергетике и электронике. Это не просто абстрактная «потеря энергии», а прямой индикатор здоровья высоковольтного оборудования. Регулярный контроль этого параметра позволяет предотвращать аварии, экономить средства на ремонте трансформаторов и кабелей, а также разрабатывать новые материалы для микроэлектроники. Понимание физики процессов, от поляризации до ионизации, дает инженеру ключ к безопасной и надежной эксплуатации энергосистем.

Нормативная база

ГОСТ 22372-77 — Материалы диэлектрические. Методы определения диэлектрической проницаемости и тангенса угла диэлектрических потерь в диапазоне частот от 100 Гц до 5 МГц.
ГОСТ 6581-75 — Материалы электроизоляционные жидкие. Методы электрических испытаний.
ГОСТ Р 55191-2012 (МЭК 60270:2000) — Методы испытаний высоким напряжением. Измерения частичных разрядов.
ПУЭ (Правила устройства электроустановок), Глава 1.8 — Нормы приемо-сдаточных испытаний. Содержит предельно допустимые значения \(\text{tg}\delta\) для трансформаторов, вводов и кабелей.
РД 34.45-51.300-97 — Объем и нормы испытаний электрооборудования. Основной документ для эксплуатирующих организаций.

Список литературы

Богородицкий Н. П., Пасынков В. В., Тареев Б. М. Электротехнические материалы: Учебник для вузов. — 7-е изд., перераб. и доп. — Л.: Энергоатомиздат, 1985. — 304 с.
Сканави Г. И. Физика диэлектриков (область слабых полей). — М.: Гостехиздат, 1949. — 500 с.
Кучинский Г. С., Кизеветтер В. Е., Пинталс Э. С. Изоляция установок высокого напряжения. — М.: Энергоатомиздат, 1987. — 368 с.