Диэлектрическая проницаемость и поляризованность вещества

Содержание страницы

1. Механизмы поляризации диэлектриков
2. Вектор поляризованности (P)
3. Связанные заряды и теорема Гаусса в диэлектрике
4. Вектор электрического смещения (D)
5. Диэлектрическая проницаемость (ε)
6. Сравнение ключевых векторов поля
7. Преимущества и недостатки диэлектриков
8. Нелинейные эффекты и сегнетоэлектрики
9. Интересные факты по теме
10. Часто задаваемые вопросы (FAQ)
Заключение

Диэлектрическая проницаемость – это основная физическая характеристика вещества, которая описывает его способность ослаблять внешнее электрическое поле. По сути, она показывает, во сколько раз сила взаимодействия между двумя зарядами в данной среде меньше, чем в вакууме. Эта величина является ключевой для понимания того, как материалы, известные как диэлектрики, реагируют на электрическое поле и накапливают электрическую энергию.

Исторически, изучение этих свойств началось в XIX веке. Майкл Фарадей был одним из первых, кто систематически исследовал влияние различных изоляционных материалов (диэлектриков) на емкость конденсаторов. Он обнаружил, что заполнение пространства между обкладками конденсатора диэлектриком увеличивает его емкость. Позднее эти идеи были формализованы Джеймсом Клерком Максвеллом, который ввел концепцию «смещения» в диэлектриках в свои знаменитые уравнения электромагнетизма. Понимание поляризации и диэлектрической проницаемости стало основой для развития электротехники, оптики и материаловедения.

Вывод: Наличие диэлектрической среды изменяет электрическое поле. Поле, создаваемое зарядом Q в веществе, всегда отличается от поля, которое тот же заряд создал бы в вакууме. Это различие обусловлено способностью атомов и молекул вещества реагировать на поле – поляризоваться.

1. Механизмы поляризации диэлектриков

Поляризация – это процесс ориентации или смещения связанных зарядов в диэлектрике под действием внешнего электрического поля. Вещества, способные к поляризации, состоят из молекул, которые можно условно разделить на два основных типа.

1.1. Неполярные молекулы (Квазиупругие диполи)

Молекулы первого типа в отсутствие внешнего поля электрически нейтральны. В них центр распределения отрицательных зарядов (электронных оболочек) совпадает с центром распределения положительных зарядов (ядер).

Однако под воздействием внешнего поля $\mathbf{E}$ эти молекулы деформируются: электронные оболочки смещаются против поля, а ядра – по полю. В результате центры зарядов расходятся, и молекула превращается в индуцированный электрический диполь. Этот диполь создает собственное внутреннее поле, направленное против внешнего, что приводит к ослаблению суммарного поля внутри вещества.

1.2. Полярные молекулы (Постоянные диполи)

Молекулы второго типа изначально асимметричны, и центры их положительных и отрицательных зарядов не совпадают даже без внешнего поля. Они уже являются диполями и характеризуются постоянным электрическим моментом диполя $\mathbf{p}$.

Электрический момент диполя – это векторная величина, определяемая как $ \mathbf{p} = q\mathbf{d} $, где $q$ – величина зарядов, а $\mathbf{d}$ – вектор смещения от отрицательного заряда к положительному. В отсутствие внешнего поля эти диполи ориентированы хаотично из-за теплового движения, и их суммарный дипольный момент в любом макроскопическом объеме равен нулю: $ \sum \mathbf{p}_j = 0 $.

При появлении внешнего поля на диполи действует вращающий момент, который стремится выстроить их по направлению поля. Этот процесс называется ориентационной поляризацией. В результате суммарный дипольный момент в объеме становится отличным от нуля: $ \sum \mathbf{p}_j \neq 0 $.

2. Вектор поляризованности (P)

Для количественной оценки степени поляризации вещества вводится векторная величина – поляризованность (или вектор поляризации), обозначаемая буквой $\mathbf{P}$.

Поляризованность определяется как предел отношения суммарного электрического дипольного момента $ \sum \mathbf{p}_j $ молекул в некотором физически малом объеме $\Delta V$ к этому объему, при его стремлении к нулю:

$$ \mathbf{P} = \lim_{\Delta V \to 0} \frac{\sum \mathbf{p}_j}{\Delta V} $$

Единица измерения поляризованности в системе СИ – Кулон на квадратный метр (Кл/м²). Поляризованность $\mathbf{P}$ представляет собой дипольный момент единицы объема вещества.

Для многих диэлектриков (в не слишком сильных полях) процесс поляризации, будь то деформация неполярных молекул или ориентация полярных, происходит тем сильнее, чем больше напряженность внешнего поля $\mathbf{E}$. Эта связь выражается линейным соотношением:

$$ \mathbf{P} = \chi_e \varepsilon_0 \mathbf{E} = \chi \mathbf{E} $$

В этой формуле коэффициент $\chi$ (читается «хи») называется абсолютной диэлектрической восприимчивостью вещества. Иногда используют безразмерную относительную восприимчивость $\chi_e$. Эти величины характеризуют, насколько легко вещество поддается поляризации.

3. Связанные заряды и теорема Гаусса в диэлектрике

Поляризация вещества имеет важное следствие. На границах диэлектрика или в объеме, где поляризация неоднородна, появляются связанные (или поляризационные) заряды. Они не являются «свободными» зарядами, как электроны в металле, а представляют собой нескомпенсированные заряды диполей.

Рассмотрим заряженное тело со свободным зарядом $Q$, помещенное в диэлектрик. Под действием поля тела диэлектрик поляризуется. Если окружить тело замкнутой поверхностью $S$, то диполи, пересекаемые этой поверхностью, будут сориентированы так, что внутри поверхности окажутся заряды, противоположные по знаку заряду $Q$ (это и есть связанные заряды $Q’$), а снаружи – заряды того же знака, что и $Q$.

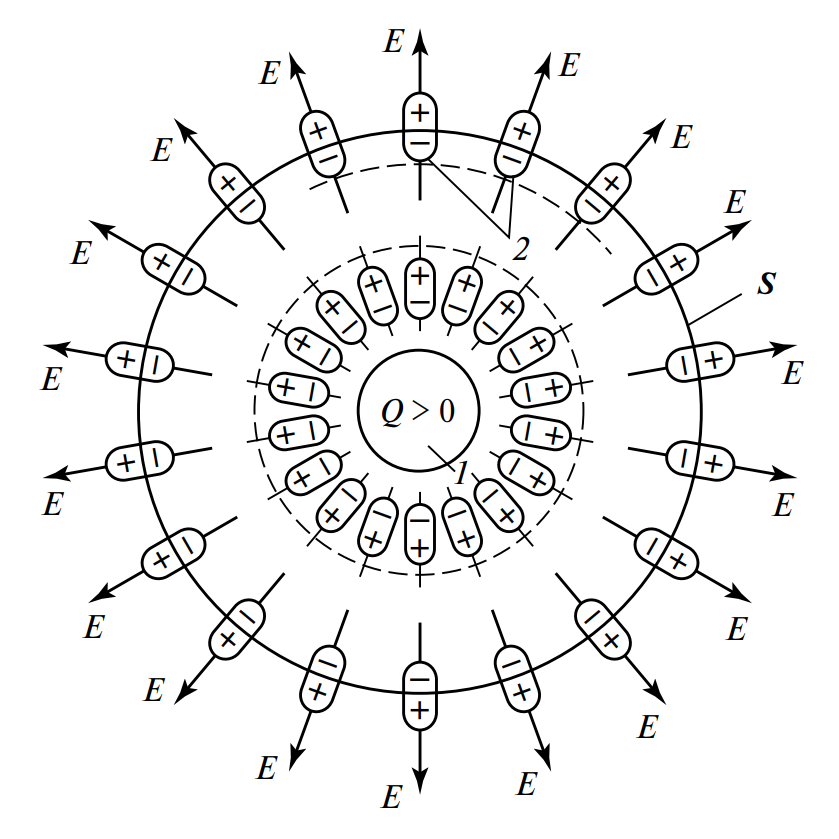
Рисунок 1. Поляризация вещества и появление связанного заряда (2) внутри поверхности S под действием свободного заряда (1).

Величина суммарного связанного заряда $Q’$ внутри замкнутой поверхности $S$ может быть рассчитана через поток вектора поляризованности $\mathbf{P}$ через эту поверхность:

$$ Q’ = -\oint_S \mathbf{P} \cdot d\mathbf{S} $$

Наличие этих связанных зарядов необходимо учитывать при применении теоремы Гаусса. Теорема Гаусса для вектора напряженности $\mathbf{E}$ в вакууме ($\oint_S \mathbf{E} \cdot d\mathbf{S} = \frac{Q_{внутр}}{\varepsilon_0}$) теперь должна учитывать *полный* заряд внутри поверхности, то есть сумму свободных ($Q$) и связанных ($Q’$) зарядов:

$$ \oint_S \mathbf{E} \cdot d\mathbf{S} = \frac{Q + Q’}{\varepsilon_0} = \frac{Q — \oint_S \mathbf{P} \cdot d\mathbf{S}}{\varepsilon_0} $$

Перенеся член с поляризованностью в левую часть, получаем:

$$ \oint_S (\varepsilon_0 \mathbf{E} + \mathbf{P}) \cdot d\mathbf{S} = Q $$

Эта запись неудобна тем, что под интегралом стоят величины, зависящие от свойств среды. Это побуждает к введению нового, вспомогательного вектора.

4. Вектор электрического смещения (D)

Выражение в скобках в формуле (5) называют вектором электрического смещения и обозначают буквой $\mathbf{D}$.

Электрическое смещение – это векторная величина, равная геометрической сумме напряженности электрического поля $\mathbf{E}$ (умноженной на электрическую постоянную $\varepsilon_0$) и поляризованности $\mathbf{P}$ в той же точке:

$$ \mathbf{D} = \varepsilon_0 \mathbf{E} + \mathbf{P} $$

Подстановка выражения (6) в (5) приводит к математической записи обобщенной теоремы Гаусса (также известной как первый постулат Максвелла для электростатики в среде):

$$ \oint_S \mathbf{D} \cdot d\mathbf{S} = Q $$

Замечание: Поток вектора электрического смещения $\mathbf{D}$ через любую замкнутую поверхность равен только свободному электрическому заряду, находящемуся внутри этой поверхности. В этом заключается фундаментальное удобство вектора $\mathbf{D}$ – он «не замечает» связанных зарядов, а определяется только внешними (свободными) источниками поля.

5. Диэлектрическая проницаемость (ε)

Теперь мы можем связать все три вектора ($\mathbf{D}$, $\mathbf{E}$, $\mathbf{P}$) вместе. Вспомним линейное соотношение (2) $\mathbf{P} = \chi \mathbf{E}$ и подставим его в определение вектора смещения (6):

$$ \mathbf{D} = \varepsilon_0 \mathbf{E} + \chi \mathbf{E} = (\varepsilon_0 + \chi) \mathbf{E} $$

Полученный коэффициент связи между векторами $\mathbf{D}$ и $\mathbf{E}$ и есть абсолютная диэлектрическая проницаемость вещества $\varepsilon$:

$$ \varepsilon = \varepsilon_0 + \chi $$

Таким образом, связь между смещением и напряженностью в линейных изотропных диэлектриках принимает простой вид:

$$ \mathbf{D} = \varepsilon \mathbf{E} $$

Абсолютная диэлектрическая проницаемость ($\varepsilon$) – это основная физическая величина, характеризующая электрические свойства диэлектрика. Она равна сумме электрической постоянной $\varepsilon_0$ (проницаемость вакуума) и диэлектрической восприимчивости $\chi$.

На практике часто используют безразмерную величину – относительную диэлектрическую проницаемость $\varepsilon_r$, которая показывает, во сколько раз проницаемость вещества больше проницаемости вакуума:

$$ \varepsilon_r = \frac{\varepsilon}{\varepsilon_0} = 1 + \frac{\chi}{\varepsilon_0} $$

Сравнивая теорему Гаусса для вакуума ($\oint_S \mathbf{E} \cdot d\mathbf{S} = \frac{Q}{\varepsilon_0}$) и для диэлектрика (используя $D = \varepsilon_r \varepsilon_0 E$), можно сделать вывод, что при том же свободном заряде $Q$ напряженность поля $\mathbf{E}$ в диэлектрике ослабевает в $\varepsilon_r$ раз по сравнению с вакуумом. Для вакуума $\varepsilon = \varepsilon_0$ и $\varepsilon_r = 1$.

6. Сравнение ключевых векторов поля

Для лучшего понимания темы, сравним характеристики трех основных векторов, описывающих электрическое поле в веществе.

Характеристика	Напряженность ($\mathbf{E}$)	Поляризованность ($\mathbf{P}$)	Электрическое смещение ($\mathbf{D}$)
Определение	Силовая характеристика поля, действующая на пробный заряд.	Дипольный момент единицы объема вещества.	Вспомогательный вектор, связанный только со свободными зарядами.
Источники поля	Все заряды (свободные + связанные).	Только связанные заряды (реакция среды).	Только свободные заряды.
Теорема Гаусса	$\oint \mathbf{E} d\mathbf{S} = (Q + Q’) / \varepsilon_0$	$\oint \mathbf{P} d\mathbf{S} = -Q’$	$\oint \mathbf{D} d\mathbf{S} = Q$
Единица (СИ)	В/м (Вольт на метр)	Кл/м² (Кулон на метр кв.)	Кл/м² (Кулон на метр кв.)
Связь (в линейной среде)	—	$\mathbf{P} = (\varepsilon — \varepsilon_0) \mathbf{E}$	$\mathbf{D} = \varepsilon \mathbf{E}$

7. Преимущества и недостатки диэлектриков

Использование материалов с различными значениями диэлектрической проницаемости имеет свои плюсы и минусы в зависимости от применения.

Преимущества диэлектриков (особенно с высокой $\varepsilon$):

Накопление энергии: Материалы с высокой $\varepsilon_r$ позволяют создавать конденсаторы большой емкости при малых размерах. Это основа миниатюризации в электронике.
Изоляция: Основная функция диэлектриков – предотвращение протекания тока (высокое удельное сопротивление).
Ослабление поля: Позволяют управлять электрическим полем, экранируя его.
Специальные эффекты: Пьезоэлектрики, пироэлектрики и сегнетоэлектрики используются в датчиках, приводах, элементах памяти.

Недостатки и ограничения:

Диэлектрические потери: При работе в переменных полях диэлектрики нагреваются из-за потерь энергии, что снижает КПД устройств.
Пробой: У каждого диэлектрика есть предел напряженности поля (электрическая прочность), при превышении которого он «пробивается» и становится проводником.
Зависимость от внешних условий: $\varepsilon$ может сильно зависеть от температуры, частоты поля, влажности и механического напряжения.
Нелинейность: При очень сильных полях связь $\mathbf{D} = \varepsilon \mathbf{E}$ перестает быть линейной.

8. Нелинейные эффекты и сегнетоэлектрики

Свойства диэлектриков и их проницаемость зависят от множества факторов: физического состояния, температуры (пироэлектрический эффект), механического давления (пьезоэлектрический эффект), освещенности (фотоэлектрический эффект). Но наиболее важной является зависимость от самой напряженности поля.

Значение $\varepsilon$ остается постоянным лишь при относительно небольших значениях $\mathbf{E}$. С ростом напряженности поля диэлектрическая проницаемость начинает нелинейно меняться, т.е. $\varepsilon(E) \neq \text{const}$.

Особенно сильно эти изменения проявляются у особого класса диэлектриков – сегнетоэлектриков. Их диэлектрическая проницаемость $\varepsilon$ при определенных условиях может достигать огромных значений (десятки тысяч) по сравнению с обычными диэлектриками ($\varepsilon_r$ от 2 до 10).

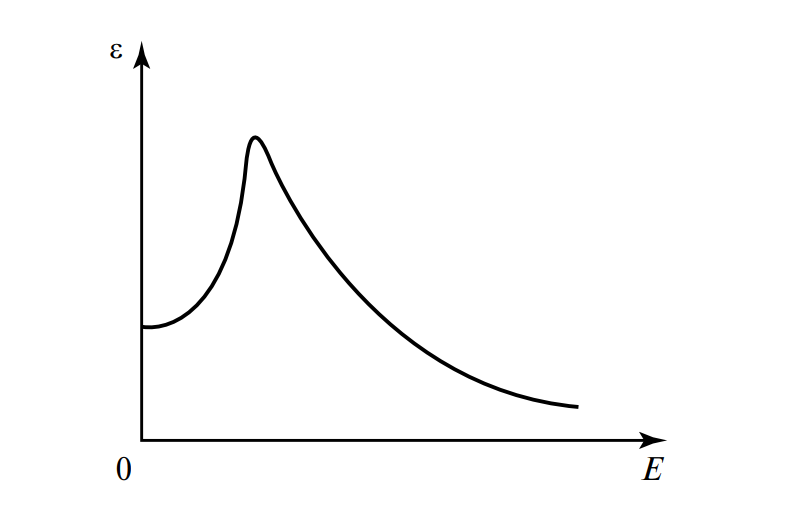
График нелинейной зависимости диэлектрической проницаемости от напряженности поля для сегнетоэлектрика, показывающий эффект насыщения

Рисунок 2. Пример нелинейной зависимости диэлектрической проницаемости $\varepsilon$ от напряженности поля $\mathbf{E}$ для сегнетоэлектриков.

Это свойство сегнетоэлектриков объясняется тем, что у них существуют целые области спонтанной (самопроизвольной) однородной поляризации, называемые доменами. Внешнее поле не столько создает диполи, сколько переориентирует целые домены, что и приводит к гигантскому отклику на поле и нелинейному поведению.

9. Интересные факты по теме

Вода как супер-диэлектрик: Относительная диэлектрическая проницаемость чистой воды $\varepsilon_r \approx 81$. Это аномально высокое значение. Именно поэтому вода является отличным растворителем для ионных соединений (как соль) – она ослабляет силы притяжения между ионами Na+ и Cl- в ~80 раз.
Зависимость от частоты: $\varepsilon_r$ – это не константа. Она сильно зависит от частоты переменного электрического поля. Для воды на высоких частотах (микроволны) $\varepsilon_r$ падает, но остается достаточно высокой, чтобы эффективно поглощать энергию, что используется в микроволновых печах.
Электрический гистерезис: Сегнетоэлектрики обладают «памятью». Зависимость поляризации $\mathbf{P}$ от поля $\mathbf{E}$ у них описывает петлю гистерезиса, аналогично зависимости намагниченности от магнитного поля у ферромагнетиков. Это свойство используется в энергонезависимой памяти (FeRAM).
Пьезо-зажигалка: В обычных пьезоэлектрических зажигалках используется пьезоэффект. Резкий механический удар по кристаллу (пьезоэлектрику) создает его сильную поляризацию и, как следствие, огромное напряжение на его гранях, достаточное для создания искры.
Вакуум – идеальный эталон: По определению, относительная диэлектрическая проницаемость вакуума $\varepsilon_r$ равна ровно 1. Воздух при нормальных условиях имеет $\varepsilon_r \approx 1.00059$, что очень близко к вакууму.

10. Часто задаваемые вопросы (FAQ)

1. Почему электрическое поле ослабевает в диэлектрике?

Под действием внешнего поля $\mathbf{E}_{внеш}$ диэлектрик поляризуется, т.е. его молекулы (или атомы) создают собственные дипольные моменты. Эти диполи создают свое внутреннее поле $\mathbf{E}_{внутр}$, которое направлено против внешнего поля. Результирующее поле внутри диэлектрика $\mathbf{E} = \mathbf{E}_{внеш} + \mathbf{E}_{внутр}$ оказывается ослабленным ($|\mathbf{E}| < |\mathbf{E}_{внеш}|$).

2. В чем практическая разница между векторами D и E?

Вектор $\mathbf{E}$ (напряженность) – это «реальная» силовая характеристика поля. Он показывает, какая сила будет действовать на заряд в данной точке, и он зависит от всех зарядов (свободных и связанных). Вектор $\mathbf{D}$ (смещение) – это вспомогательный вектор, введенный для удобства. Он зависит только от свободных зарядов. На границе двух диэлектриков $\mathbf{E}$ испытывает скачок (из-за появления связанных зарядов), а $\mathbf{D}$ (в отсутствие свободных зарядов на границе) остается непрерывным (точнее, его нормальная компонента).

3. Что такое диэлектрическая восприимчивость $\chi$?

Восприимчивость $\chi$ – это мера того, насколько «охотно» вещество поляризуется. Она напрямую связывает отклик вещества (поляризованность $\mathbf{P}$) с причиной (полем $\mathbf{E}$) через формулу $\mathbf{P} = \chi \mathbf{E}$. Чем выше $\chi$, тем сильнее поляризуется материал в том же самом поле, и тем выше будет его диэлектрическая проницаемость ($\varepsilon = \varepsilon_0 + \chi$).

4. Что такое «сегнетоэлектрик» (Ferroelectric)?

Сегнетоэлектрик – это особый тип диэлектрика, который обладает спонтанной (самопроизвольной) поляризацией даже в отсутствие внешнего поля. Эта поляризация существует в областях-доменах. Под действием внешнего поля эти домены могут переориентироваться, что приводит к очень высоким значениям $\varepsilon_r$ и нелинейному поведению, включая гистерезис. Название происходит от Сегнетовой соли – первого открытого материала с такими свойствами.

5. Где на практике используются материалы с высокой $\varepsilon$?

Основное применение – многослойные керамические конденсаторы (MLCC), которые являются «рабочими лошадками» современной электроники. Их можно найти в любом устройстве, от смартфона до автомобиля. Благодаря высокой $\varepsilon_r$ (тысячи и десятки тысяч) сегнетоэлектрической керамики (например, титаната бария BaTiO₃), можно получить огромную емкость в очень маленьком объеме. Они также используются в элементах памяти (FeRAM) и пьезодатчиках.

Заключение

Понятия поляризованности и диэлектрической проницаемости являются краеугольными в физике диэлектриков и электродинамике сплошных сред. Способность вещества реагировать на внешнее электрическое поле, создавая внутреннее встречное поле, коренным образом изменяет электростатические взаимодействия.

Введение векторов поляризованности $\mathbf{P}$ (отклик среды) и электрического смещения $\mathbf{D}$ (связь со свободными зарядами) позволяет корректно описать поле в веществе с помощью обобщенной теоремы Гаусса. Ключевые характеристики среды – диэлектрическая восприимчивость $\chi$ и проницаемость $\varepsilon$ – связывают эти векторы с напряженностью $\mathbf{E}$ и определяют все инженерные применения диэлектриков: от простой изоляции проводов до создания сверхъемких конденсаторов и элементов памяти на основе сегнетоэлектриков.

Нормативные документы

Определение и методы измерения диэлектрической проницаемости стандартизированы. Ключевые действующие стандарты в этой области:

ГОСТ 21515-76 «Материалы диэлектрические. Термины и определения.» – Устанавливает основные термины и определения, включая «диэлектрическая проницаемость» и «поляризация».
ГОСТ 22372-77 «Материалы электроизоляционные. Методы определения диэлектрической проницаемости и тангенса угла диэлектрических потерь в диапазоне частот от 100 до 5000000 Гц.» – Описывает классические методы измерения $\varepsilon_r$ в широком диапазоне частот.