Расчет действующих значений и мощности несинусоидального тока

Содержание страницы

1. Расчет действующих и средних значений
2. Коэффициенты, характеризующие форму несинусоидальных кривых
3. Мощность в цепях несинусоидального тока
4. Сравнение основных характеристик сигнала
5. Проблемы несинусоидальности
6. Интересные факты о несинусоидальных сигналах
7. Часто задаваемые вопросы (FAQ)
Заключение

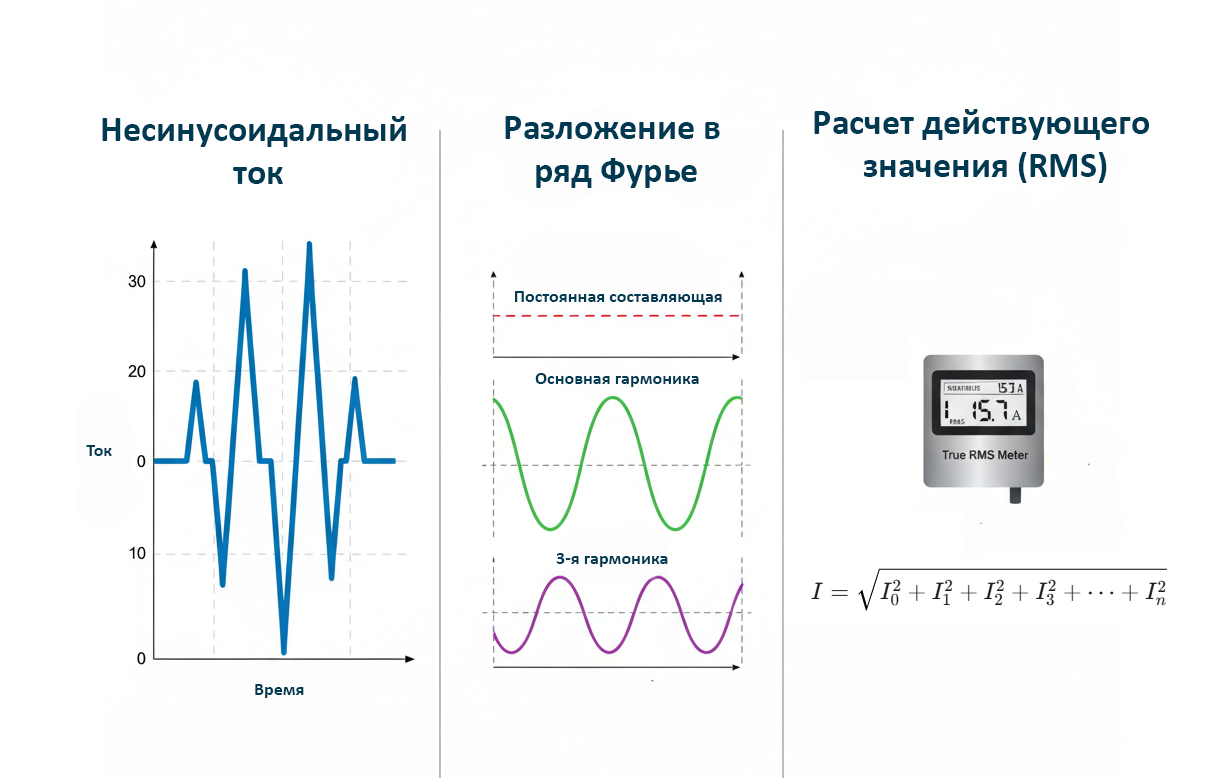
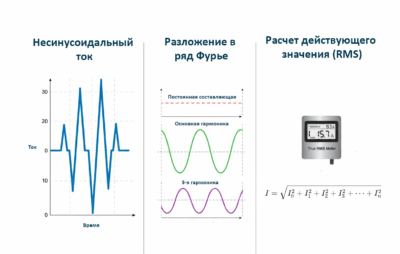
В современных электрических цепях форма тока и напряжения часто отличается от идеальной синусоиды. Это явление, известное как несинусоидальность, возникает из-за наличия нелинейных нагрузок, таких как выпрямители, импульсные источники питания, частотные преобразователи и люминесцентные лампы. Такие сигналы называются периодическими несинусоидальными величинами.

Исторически, расчеты электрических цепей велись в предположении чистой синусоидальной формы сигналов. Однако с массовым распространением силовой электроники и цифровых устройств, начиная со второй половины XX века, искажение формы стало повсеместной проблемой. Для корректного анализа таких цепей, расчета мощностей, потерь и тепловых режимов работы оборудования необходимо использовать специальные методы, основанные на разложении несинусоидальных сигналов в ряд Фурье и определении их интегральных характеристик — действующих и средних значений.

1. Расчет действующих и средних значений

Любую периодическую несинусоидальную функцию $i(t)$ (или $u(t)$), удовлетворяющую условиям Дирихле, можно представить в виде ряда Фурье — суммы постоянной составляющей и бесконечного ряда синусоидальных гармоник:

$$ i(t) = I_0 + \sum_{k=1}^{\infty} I_{km} \sin(k\omega t + \phi_k) $$

Здесь $I_0$ — постоянная составляющая (среднее значение), $I_{km}$ — амплитуда $k$-й гармоники, $\omega$ — основная (фундаментальная) угловая частота, а $\phi_k$ — начальная фаза $k$-й гармоники.

1.1. Действующее (среднеквадратичное) значение

Действующее (эффективное) значение периодического тока определяется как его среднеквадратичное значение за период $T$. Физический смысл действующего значения заключается в том, что оно равно величине такого постоянного тока, который, протекая через то же сопротивление $R$, выделял бы за один период $T$ то же количество теплоты, что и данный периодический ток.

Его можно определить путем непосредственного интегрирования квадрата мгновенных значений. Квадрат действующего значения $I^2$ равен:

$$ I^2 = \frac{1}{T} \int_{0}^{T} [i(t)]^2 dt $$

Если известен спектральный состав тока (т.е. его разложение в ряд Фурье), действующее значение можно вычислить по амплитудам (или действующим значениям) всех его синусоидальных составляющих.

Подставим ряд Фурье для $i(t)$ в интеграл. Квадрат тока $[i(t)]^2$ будет содержать сумму квадратов всех слагаемых (постоянной составляющей и всех гармоник) и сумму членов, содержащих произведения синусоид с разными частотами (например, $\sin(\omega t) \cdot \sin(2\omega t)$).

Благодаря свойству ортогональности тригонометрических функций, интеграл за период от произведения синусоид с разными частотами всегда равен нулю. Поэтому отличной от нуля будет только сумма интегралов от квадратов постоянной составляющей и каждой синусоидальной гармоники.

Каждый такой интеграл от квадрата синусоиды равен квадрату ее действующего значения. Напомним, что действующее значение $k$-й гармоники $I_k$ связано с ее амплитудой $I_{km}$ как $I_k = \frac{I_{km}}{\sqrt{2}}$.

Таким образом, общее действующее значение $I$ несинусоидального тока равно:

$$ I = \sqrt{I_0^2 + I_1^2 + I_2^2 + \dots + I_k^2 + \dots} = \sqrt{\sum_{k=0}^{\infty} I_k^2} \quad (1) $$

где $I_0$ — постоянная составляющая, а $I_1, I_2, \dots, I_k$ — действующие значения 1-й (основной), 2-й и $k$-й гармоник соответственно.

Аналогичные формулы и выводы полностью справедливы и для напряжений. Действующее значение несинусоидального напряжения $U$ равно:

$$ U = \sqrt{U_0^2 + U_1^2 + U_2^2 + \dots + U_k^2 + \dots} = \sqrt{\sum_{k=0}^{\infty} U_k^2} \quad (2) $$

1.2. Среднее и средневыпрямленное значение

Помимо действующего значения, в электротехнике используются и другие усредненные характеристики.

Среднее значение за период (или постоянная составляющая) определяется по общему правилу нахождения среднего значения функции:

$$ I_{ср} = \frac{1}{T} \int_{0}^{T} i(t) dt $$

Эта величина в точности равна $I_0$ — нулевому члену при разложении в ряд Фурье. Для сигнала без постоянного смещения (например, идеальной синусоиды) среднее значение равно нулю.

Среднее по модулю (средневыпрямленное) значение также применяется в расчетах, особенно связанных с выпрямительными устройствами. Оно определяется как среднее значение модуля мгновенной величины за период:

$$ I_{ср.мод} = \frac{1}{T} \int_{0}^{T} |i(t)| dt $$

Многие простые (не «True RMS») мультиметры измеряют именно эту величину, но их шкала откалибрована для отображения действующего значения синусоидального сигнала. При измерении несинусоидальных токов такие приборы дают неверные показания.

2. Коэффициенты, характеризующие форму несинусоидальных кривых

Для численной оценки степени отличия периодической кривой от идеальной синусоиды, а также для описания ее специфических характеристик, в электротехнике и электронике используют ряд безразмерных коэффициентов. Эти коэффициенты особенно важны при анализе качества электроэнергии и при выборе измерительной аппаратуры.

В расчетах (если не указано иное) предполагается, что кривая симметрична относительно оси абсцисс, то есть ее постоянная составляющая ($U_0$) равна нулю.

2.1. Коэффициент формы (kф)

Коэффициент формы — это отношение действующего (RMS) значения величины к ее средневыпрямленному (среднему по модулю) значению.

$$ k_ф = \frac{U_{RMS}}{U_{ср.мод}} $$

Этот коэффициент показывает «наполненность» графика кривой. Для идеальной синусоиды он имеет эталонное значение:

$$ k_{ф(синус)} = \frac{U_m / \sqrt{2}}{2U_m / \pi} = \frac{\pi}{2\sqrt{2}} \approx 1.11 $$

Для прямоугольного сигнала (меандра) $k_ф = 1$, так как действующее значение равно среднему по модулю.

2.2. Коэффициент амплитуды (kа) или Крест-фактор

Коэффициент амплитуды (также известный как крест-фактор) — это отношение максимального (амплитудного) значения величины к ее действующему (RMS) значению.

$$ k_а = \frac{U_{max}}{U_{RMS}} $$

Этот коэффициент характеризует «пиковость» сигнала. Он критически важен для оценки пиковых нагрузок на диоды в выпрямителях, а также для определения пробивного напряжения изоляции. Для идеальной синусоиды он равен:

$$ k_{а(синус)} = \frac{U_m}{U_m / \sqrt{2}} = \sqrt{2} \approx 1.41 $$

Сигналы с высоким крест-фактором (например, короткие импульсы тока, потребляемые импульсными блоками питания) требуют особого внимания, так как их пиковое значение значительно превышает действующее.

2.3. Коэффициенты гармонических искажений (kи и kг)

Эти коэффициенты напрямую оценивают степень несинусоидальности кривой, то есть долю высших гармоник в ее составе.

Коэффициент искажения (kи)
Определяется как отношение действующего значения основной (первой) гармоники к полному действующему значению всей кривой:

$$ k_и = \frac{U_1}{U_{RMS}} = \frac{U_1}{\sqrt{U_1^2 + U_2^2 + U_3^2 + \dots}} $$

Этот коэффициент показывает, какая доля общей энергии сигнала приходится на полезную первую гармонику. Для чистой синусоиды $k_и = 1$.

Коэффициент гармоник (kг) или THD (Total Harmonic Distortion)
В электронике и радиотехнике (а в последнее время и в энергетике) чаще используется Коэффициент гармонических составляющих (или Суммарный коэффициент гармонических составляющих, THD). Он определяется как отношение действующего значения суммы всех высших гармоник к действующему значению основной (первой) гармоники:

$$ k_г \text{ (THD)} = \frac{\sqrt{\sum_{k=2}^{\infty} U_k^2}}{U_1} $$

Для чистой синусоиды $k_г = 0$.

Примечание: Корректная связь между kи и kг

В некоторых источниках встречается ошибочная формула связи $k_и^2 = 1 — k_г^2$. Эта ошибка возникает из-за путаницы в определениях (к чему относится знаменатель в $k_г$).

Приведенные выше определения являются стандартными. Правильная связь между ними (при $U_0=0$) выводится следующим образом:

Из формулы полного RMS: $U_{RMS}^2 = U_1^2 + \sum_{k=2}^{\infty} U_k^2$
Из определения $k_г$, имеем: $\sum_{k=2}^{\infty} U_k^2 = (k_г \cdot U_1)^2$
Подставляем (2) в (1): $U_{RMS}^2 = U_1^2 + (k_г \cdot U_1)^2 = U_1^2 \cdot (1 + k_г^2)$
Из определения $k_и$, имеем: $k_и^2 = \frac{U_1^2}{U_{RMS}^2}$
Подставляем (3) в (4): $k_и^2 = \frac{U_1^2}{U_1^2 \cdot (1 + k_г^2)} = \frac{1}{1 + k_г^2}$

Таким образом, правильная формула связи: $k_и = \frac{1}{\sqrt{1 + k_г^2}}$

2.4. Понятие «Практически синусоидальной» кривой и ГОСТ

Кривые напряжения в промышленных сетях всегда в той или иной степени отличаются от идеальной синусоиды. В электроэнергетике вводится понятие практически синусоидальной кривой.

Ранее, напряжение считалось практически синусоидальным, если суммарный коэффициент гармонических составляющих (THD или $k_г$) не превышал 5%.

Согласно действующему ГОСТ 32144-2013 («Электрическая энергия… Нормы качества…»), нормируется Суммарный коэффициент гармонических составляющих напряжения (THD_U или K_U). Для сетей низкого напряжения (0,38 кВ) нормальное предельное значение для этого коэффициента (K_U) составляет 8%. Таким образом, современный стандарт допускает несколько большие искажения формы напряжения.

2.5. Влияние формы кривой на результаты измерений

Использование измерительных приборов, не предназначенных для несинусоидальных сигналов, приводит к грубым ошибкам. Это связано именно с тем, что $k_ф$ и $k_а$ для искаженной кривой отличаются от «зашитых» в прибор синусоидальных значений.

Приборы электромагнитной, электродинамической и тепловой систем (например, старые стрелочные амперметры) реагируют на тепловое действие тока. Они корректно измеряют истинное действующее значение (True RMS) независимо от формы кривой.
Магнитоэлектрические приборы (основной тип стрелочных приборов) сами по себе измеряют только постоянную составляющую (среднее значение).
Выпрямительные приборы (большинство недорогих цифровых мультиметров) работают по принципу: измеряют средневыпрямленное значение ($U_{ср.мод}$), а затем умножают его на коэффициент формы синусоиды ($\approx 1.11$), чтобы показать на дисплее якобы «действующее» значение.
Амплитудные электронные вольтметры измеряют пиковое значение ($U_{max}$) и делят его на коэффициент амплитуды синусоиды ($\approx 1.41$), также показывая «действующее» значение.

Если таким мультиметром (выпрямительным или амплитудным) измерять напряжение, форма которого не является синусоидой (например, на выходе ИБП или за диммером), его показания будут неверными, так как реальные $k_ф$ и $k_а$ сигнала не равны 1.11 и 1.41. Для корректных измерений в таких цепях необходимо использовать приборы с функцией «True RMS».

3. Мощность в цепях несинусоидального тока

Наличие высших гармоник в спектре тока и напряжения существенно усложняет расчеты мощности в цепи.

3.1. Активная мощность

Активная мощность $P$ по определению равна среднему значению мгновенной мощности $p(t) = u(t) \cdot i(t)$ за период $T$:

$$ P = \frac{1}{T} \int_{0}^{T} p(t) dt = \frac{1}{T} \int_{0}^{T} u(t) i(t) dt $$

Подставим в это выражение ряды Фурье для $u(t)$ и $i(t)$:

$$ P = \frac{1}{T} \int_{0}^{T} [U_0 + \sum_{n=1}^{\infty} U_{nm} \sin(n\omega t + \beta_n)] \cdot [I_0 + \sum_{k=1}^{\infty} I_{km} \sin(k\omega t + \alpha_k)] dt $$

Как и при расчете действующего значения, из-за ортогональности синусоид интеграл за период от произведения гармоник тока и напряжения *разных* частот (где $n \neq k$) равен нулю. Активная мощность передается только между гармониками с одинаковыми частотами.

Таким образом, остаются только сумма интегралов от произведений гармоник тока и напряжений одинаковой частоты (включая $n=k=0$ для постоянной составляющей). Каждый из таких интегралов определяет активную мощность для соответствующей гармоники:

Для постоянной составляющей: $P_0 = U_0 I_0$

Для $n$-й гармоники: $P_n = \frac{U_{nm} I_{nm}}{2} \cos(\beta_n — \alpha_n) = U_n I_n \cos(\phi_n)$, где $\phi_n = \beta_n — \alpha_n$ — сдвиг фаз между $n$-й гармоникой напряжения и тока.

Полная активная мощность в цепи равна сумме активных мощностей всех гармонических составляющих:

$$ P = P_0 + P_1 + P_2 + \dots = U_0 I_0 + \sum_{n=1}^{\infty} U_n I_n \cos(\phi_n) \quad (3) $$

3.2. Реактивная, полная мощность и коэффициент мощности

Аналогично вводится понятие реактивной мощности $Q$. Однако здесь существует несколько подходов. По классической теории (теории Фризе), реактивная мощность определяется как сумма реактивных мощностей отдельных гармоник:

$$ Q = \sum_{n=1}^{\infty} Q_n = \sum_{n=1}^{\infty} U_n I_n \sin(\phi_n) $$

Обратите внимание, что постоянная составляющая ($n=0$) не создает реактивной мощности.

Полная мощность $S$ определяется как произведение общего действующего значения напряжения $U$ и общего действующего значения тока $I$:

$$ S = U \cdot I $$

где $U$ и $I$ рассчитываются по формулам (1) и (2).

Ключевое отличие несинусоидальной цепи от синусоидальной заключается в том, что $S^2 \neq P^2 + Q^2$.

Примечание: Мощность искажения (T)

В несинусоидальных цепях «недостающая» часть полной мощности называется мощностью искажения (T или D). Она возникает из-за взаимодействия гармоник напряжения одной частоты с гармониками тока другой частоты, которые не создают активной мощности, но создают дополнительную нагрузку на сеть.

Полный баланс мощностей (согласно теории Будяну) выглядит так:

$$ S^2 = P^2 + Q^2 + T^2 $$

Мощность искажения $T$ равна нулю только тогда, когда либо напряжение, либо ток являются чистыми синусоидами.

Коэффициент мощности ($k_M$) (Power Factor, PF) представляет собой отношение активной мощности $P$ к полной мощности $S$:

$$ k_M = \frac{P}{S} $$

Из-за наличия мощности искажения $T$, в несинусоидальных цепях коэффициент мощности $k_M$ всегда меньше, чем $\cos(\phi_1)$ (коэффициент мощности основной гармоники).

$$ k_M = \frac{P}{S} = \frac{\sum P_n}{U \cdot I} \neq \cos(\phi_1) $$

3.3. Метод эквивалентных синусоид

Для приближенных расчетов цепей при несинусоидальных токах, когда доля высших гармоник не очень большая, иногда применяют метод эквивалентных синусоид. При этом считают, что действующие значения эквивалентных синусоид равны полным действующим значениям несинусоидальных токов и напряжений, т. е.:

$$ I_Э = I = \sqrt{I_0^2 + I_1^2 + \dots} $$
$$ U_Э = U = \sqrt{U_0^2 + U_1^2 + \dots} $$

А фазовый сдвиг $\phi_Э$ между ними принимается таким, чтобы обеспечить правильную активную мощность $P$:

$$ \phi_Э = \arccos\left(\frac{P}{U \cdot I}\right) = \arccos(k_M) $$

Этот метод является упрощением, так как он не учитывает разное поведение элементов цепи (особенно $L$ и $C$) на разных частотах.

4. Сравнение основных характеристик сигнала

Для наглядности сведем ключевые параметры несинусоидального сигнала в таблицу.

Параметр	Определение	Расчетная формула (через гармоники)	Физический смысл / Применение
Действующее (RMS)	Среднеквадратичное значение за период.	$ I = \sqrt{\sum_{k=0}^{\infty} I_k^2} $	Эквивалентное тепловое действие. Основная величина для расчетов потерь, нагрузочной способности кабелей и предохранителей.
Среднее	Среднеарифметическое значение за период.	$ I_{ср} = I_0 $	Постоянная составляющая (DC-смещение). Важно для трансформаторов (может вызвать насыщение) и в цепях постоянного тока.
Средневыпрямленное	Среднее значение модуля функции за период.	$ I_{ср.мод} = \frac{1}{T} \int_{0}^{T} \|i(t)\| dt $	Используется в анализе выпрямителей. Измеряется простыми мультиметрами.

5. Проблемы несинусоидальности

Расчет действующих и средних значений — это не просто математическое упражнение, а насущная инженерная задача.

Преимущества корректного расчета

Правильный выбор оборудования: Только RMS-значение позволяет корректно выбрать сечение кабелей, номиналы автоматов защиты и трансформаторов, так как их нагрев зависит именно от действующего значения тока.
Оценка качества электроэнергии: Расчеты позволяют определить уровень гармонических искажений, который нормируется стандартами (например, ГОСТ 32144-2013).
Точный учет потерь: Потери в проводниках ($P = I^2R$) и в магнитопроводах (зависят от частоты) можно рассчитать, только зная весь гармонический состав.
Диагностика проблем: Высокие значения высших гармоник могут указывать на неисправность оборудования или неправильную работу нелинейных нагрузок.

Проблемы несинусоидальности

Дополнительные потери: Высшие гармоники тока, протекая по активным сопротивлениям, создают дополнительные потери тепла, снижая КПД системы.
Перегрев оборудования: Нейтральный провод в трехфазных системах может быть перегружен токами третьей гармоники (они складываются, а не вычитаются). Трансформаторы и двигатели испытывают повышенный нагрев из-за потерь на вихревые токи, растущих с частотой.
Электромагнитные помехи: Высокочастотные гармоники создают помехи для оборудования связи и систем автоматики.
Резонансные явления: Гармоники могут войти в резонанс с емкостями (например, конденсаторными батареями) и индуктивностями сети, вызывая резкое возрастание токов и напряжений.
Снижение коэффициента мощности: Из-за мощности искажения $T$ общий коэффициент мощности $P/S$ снижается, что требует от сети «прокачивать» большую полную мощность $S$ для передачи той же полезной активной мощности $P$.

6. Интересные факты о несинусоидальных сигналах

«True RMS»: Аббревиатура RMS (Root Mean Square) — это английское название для «среднеквадратичного» (действующего) значения. Обычные мультиметры измеряют средневыпрямленное значение и показывают RMS, умножая его на 1.11 (коэффициент для синусоиды). Для несинусоидальных сигналов они врут. Только приборы с пометкой «True RMS» выполняют честное среднеквадратичное вычисление и показывают правильный результат.
Гармоники — «загрязнители» сети: Нелинейные нагрузки (как компьютеры) не «потребляют» гармоники из сети, а сами *генерируют* их и «сбрасывают» обратно в сеть, искажая напряжение для других потребителей.
Проблема 3-й гармоники: В симметричной трехфазной системе токи основных (первых) гармоник в нейтрали взаимно компенсируются. Однако токи 3-й, 9-й и других гармоник, кратных трем, в трех фазах совпадают по фазе и *складываются* в нейтральном проводе. Это может привести к его перегреву, даже если фазные нагрузки кажутся нормальными.
«Плохой» Power Factor при «хорошем» $\cos(\phi_1)$: Импульсный блок питания может потреблять ток почти без сдвига фаз ($\cos(\phi_1) \approx 1$), но в виде коротких импульсов. Из-за огромного уровня гармоник его полный коэффициент мощности $k_M = P/S$ может быть очень низким (0.5–0.7).
Мощность искажения: Концепция разделения полной мощности на P, Q и T (мощность искажения) была предложена румынским инженером Константином Будяну (Constantin Budeanu) еще в 1927 году.
Нулевая активная мощность: Если к идеальному конденсатору приложить несинусоидальное напряжение, он будет потреблять ток, гармонический состав которого отличается от напряжения (т.к. $Z_c = 1/(j\omega C)$ зависит от частоты). При этом активная мощность $P$ будет равна нулю, но полная мощность $S$ и мощность искажения $T$ будут существовать.
Источник проблемы: До 1970-х годов основной нелинейной нагрузкой были ртутные выпрямители. Широкое распространение полупроводниковых диодов, тиристоров и транзисторов в силовой электронике привело к тому, что проблема гармоник стала одной из ключевых в современной энергетике.

7. Часто задаваемые вопросы (FAQ)

1. Что такое несинусоидальный ток?

Это любой периодический ток, форма которого на графике отличается от идеальной синусоиды. Математически это означает, что помимо основной (первой) гармоники, он содержит постоянную составляющую ($I_0$) и/или высшие гармоники (2-ю, 3-ю, 4-ю и т.д.).

2. Почему действующее (RMS) значение важнее среднего?

Потому что нагрев проводов, обмоток двигателей и трансформаторов пропорционален квадрату тока ($P = I^2R$). Именно действующее (среднеквадратичное) значение отражает эту тепловую мощность. Среднее значение ($I_0$) показывает только наличие постоянной составляющей, которая для большинства цепей переменного тока равна нулю или близка к нему.

3. Что такое «True RMS» мультиметр?

Это измерительный прибор, который вычисляет истинное среднеквадратичное (действующее) значение измеряемого сигнала. Он корректно измеряет RMS как для чистой синусоиды, так и для сложных несинусоидальных сигналов (например, на выходе частотного преобразователя или за диммером). Обычные (не-True RMS) приборы врут на несинусоидальных сигналах.

4. Почему $S^2 \neq P^2 + Q^2$ в несинусоидальных цепях?

Потому что в цепи появляется третья компонента — мощность искажения ($T$). Она возникает из-за наличия гармоник. Полная мощность $S$ учитывает все гармоники тока и напряжения, в то время как активная $P$ и реактивная $Q$ (в классическом определении) представляют собой лишь суммы мощностей *на каждой гармонике*. Полный баланс: $S^2 = P^2 + Q^2 + T^2$.

5. Что такое коэффициент мощности (Power Factor) в цепи с гармониками?

Это отношение активной (полезной) мощности $P$ ко всей полной мощности $S$, «забираемой» из сети ($k_M = P/S$). Он всегда меньше или равен 1. В несинусоидальных цепях он состоит из двух «со-множителей»: коэффициента сдвига ($\cos(\phi_1)$) и коэффициента искажений ($k_{dist}$). Низкий $k_M$ (даже при $\cos(\phi_1) \approx 1$) означает, что нагрузка создает много гармоник, «загрязняя» сеть.

6. Какие устройства создают гармоники?

Любые устройства с нелинейной вольт-амперной характеристикой. Главные «генераторы» гармоник в быту и промышленности — это: импульсные блоки питания (компьютеры, телевизоры, зарядные устройства), светодиодные и люминесцентные лампы с электронным балластом, частотно-регулируемые приводы (ЧРП) электродвигателей, выпрямители, сварочные аппараты.

7. Чем опасны высшие гармоники в электросети?

Они вызывают дополнительный нагрев проводов (особенно нейтрали) и трансформаторов, вибрацию и преждевременный износ двигателей, приводят к ложному срабатыванию защитной автоматики, создают помехи для систем связи и могут вызвать резонанс в сети, приводящий к аварийным перенапряжениям.

Заключение

Понимание и корректный расчет действующих и средних значений несинусоидальных токов и напряжений являются фундаментальной задачей современной электротехники и энергетики. В отличие от идеализированных синусоидальных цепей, наличие высших гармоник требует применения анализа на основе рядов Фурье.

Ключевым параметром для оценки тепловых нагрузок является действующее (RMS) значение, которое вычисляется как корень из суммы квадратов всех гармонических составляющих. Расчет мощности также усложняется: полная активная мощность равна сумме активных мощностей по каждой гармонике, однако полная мощность $S$ становится больше, чем $ \sqrt{P^2 + Q^2} $ из-за появления мощности искажения $T$. Это приводит к снижению общего коэффициента мощности $P/S$ и падению эффективности системы электроснабжения.

Нормативные документы

Анализ и нормирование несинусоидальности токов и напряжений в электрических сетях Российской Федерации регламентируется следующими основными действующими стандартами:

ГОСТ 32144-2013 «Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения».
ГОСТ 30804.4.7-2013 (IEC 61000-4-7:2009) «Совместимость технических средств электромагнитная. Общее руководство по средствам измерений и измерениям гармоник и интергармоник для систем электроснабжения и подключаемых к ним технических средств».
ГОСТ 30804.4.30-2013 (IEC 61000-4-30:2008) «Электрическая энергия. Совместимость технических средств электромагнитная. Методы измерений показателей качества электрической энергии».

Действующее и среднее значение несинусоидальных токов и напряжений: расчет, формулы, коэффициенты