Резонанс токов в электрических цепях: теория и рачет

Содержание страницы

Физическая природа явления и математическое описание
Пример расчета
Сравнение: Резонанс токов vs Резонанс напряжений
Преимущества и недостатки использования резонанса токов
Интересные факты о резонансе
Часто задаваемые вопросы (FAQ)
Заключение

Резонанс токов — это особое явление в электрической цепи с параллельным соединением индуктивности и емкости, при котором реактивная составляющая проводимости цепи становится равной нулю. В этот момент ток источника совпадает по фазе с напряжением, а внутри контура возникают токи, значительно превышающие ток источника.

Краткая история: Теоретические основы резонанса были заложены лордом Кельвином (Уильямом Томсоном) в 1853 году, когда он вывел уравнение для колебательного контура. Позже Джеймс Клерк Максвелл и Генрих Герц экспериментально подтвердили эти явления, что стало фундаментом для создания радиосвязи, где параллельный резонанс (или «колебательный контур») используется для настройки на нужную частоту по сей день.

Физическая природа явления и математическое описание

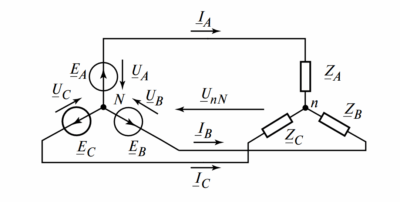
Резонанс токов, или параллельный резонанс, может возникнуть в цепи с двумя параллельными ветвями, когда в одной из них включены элементы \( R_1 \) и \( L \), а в другой — \( R_2 \) и \( C \). На рисунке 1 представлена схема с такими ветвями.

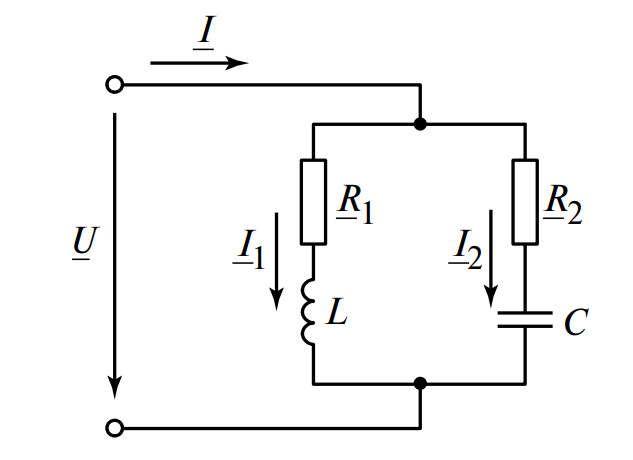
Рис. 1. Параллельный RLC-контур (схема ветвей)

Рассмотрим математическую модель данной цепи. Сопротивление ветви с элементами \( R_1 \) и \( L \):

\underline{Z}_1 = R_1 + j\omega L

Сопротивление ветви с элементами \( R_2 \) и \( C \):

\underline{Z}_2 = R_2 — j\frac{1}{\omega C}

Для анализа параллельных цепей удобнее использовать проводимости. Проводимость первой ветви \( \underline{Y}_1 \):

\underline{Y}_1 = \frac{1}{\underline{Z}_1} = \frac{1}{R_1 + j\omega L} = \frac{R_1 — j\omega L}{R_1^2 + (\omega L)^2} = G_1 — jB_1

Где \( G_1 = \frac{R_1}{R_1^2 + (\omega L)^2} \) — активная проводимость, а \( B_1 = \frac{\omega L}{R_1^2 + (\omega L)^2} \) — индуктивная проводимость.

Проводимость второй ветви \( \underline{Y}_2 \):

\underline{Y}_2 = \frac{1}{\underline{Z}_2} = \frac{1}{R_2 — j\frac{1}{\omega C}} = \frac{R_2 + j\frac{1}{\omega C}}{R_2^2 + (\frac{1}{\omega C})^2} = G_2 + jB_2

Где \( G_2 \) — активная проводимость, а \( B_2 \) — емкостная проводимость.

Аналогия для понимания: Представьте резонанс токов как качели, которые вы подталкиваете. Ветвь с катушкой и ветвь с конденсатором — это как движение качелей вперед и назад. В момент резонанса они обмениваются энергией между собой идеально синхронно, и вам (источнику тока) нужно лишь немного подпитывать систему, чтобы компенсировать трение (сопротивления R).

Условие возникновения резонанса

Резонанс наступает, когда реактивная проводимость всей цепи равна нулю. Условие резонанса выражается равенством реактивных проводимостей ветвей:

Im(\underline{Y}) = B_2 — B_1 = 0 \quad \text{или} \quad \frac{\omega L}{R_1^2 + (\omega L)^2} = \frac{1/\omega C}{R_2^2 + (1/\omega C)^2}

Из этого уравнения выводится формула резонансной частоты \( \omega_p \):

\omega_p = \frac{1}{\sqrt{LC}} \sqrt{\frac{L/C — R_1^2}{L/C — R_2^2}}

В полученном выражении величина \( \rho = \sqrt{\frac{L}{C}} \) называется характеристическим сопротивлением параллельного контура.

Важно: Формула показывает, что возникновения резонанса токов можно добиться, изменяя частоту источника или параметры \( R_1, R_2, L, C \). Однако резонанс возможен только если характеристическое сопротивление \( \rho \) больше обоих активных сопротивлений (\( R_1 \) и \( R_2 \)) или меньше обоих одновременно. В противном случае подкоренное выражение станет отрицательным, и резонанс невозможен.

Особый случай: Безразличный резонанс

При условии, что \( R_1 = R_2 = \rho \), дробь под корнем становится неопределенностью вида 0/0. В этом случае резонансная частота может иметь любое значение. Иначе говоря, наблюдается безразличный (к частоте) резонанс.

Входная проводимость цепи при резонансе носит чисто активный характер. Резонансный ток на входе цепи минимален и определяется суммой активных проводимостей:

\( I = Y_p U = (G_1 + G_2)U \)

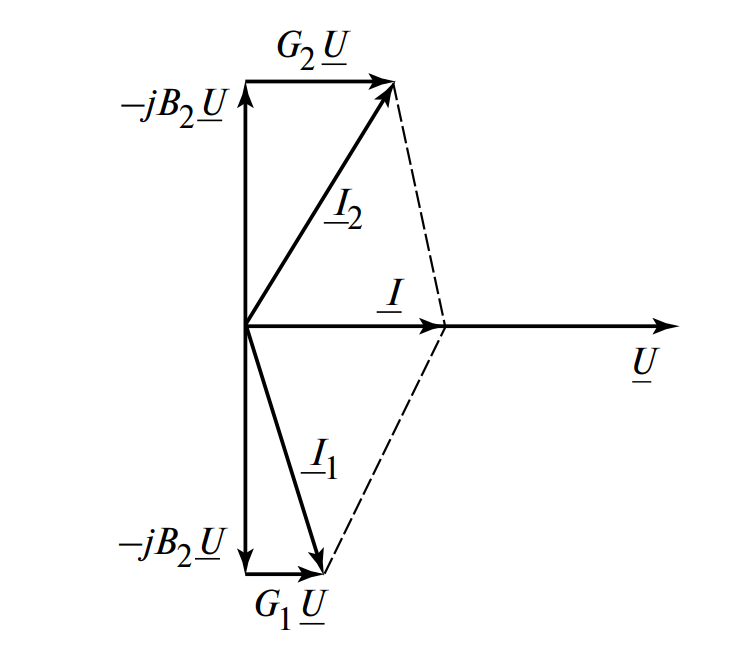
Векторная диаграмма при резонансе токов, показывающая компенсацию реактивных составляющих, приведена на рис. 2.

Рис. 2. Векторная диаграмма при резонансе токов. Видно, что общий ток I совпадает по фазе с напряжением U.

Пример расчета

Рассмотрим практическую задачу для закрепления материала.

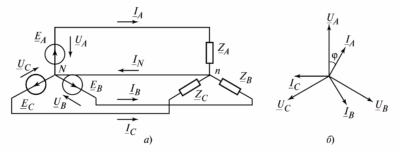
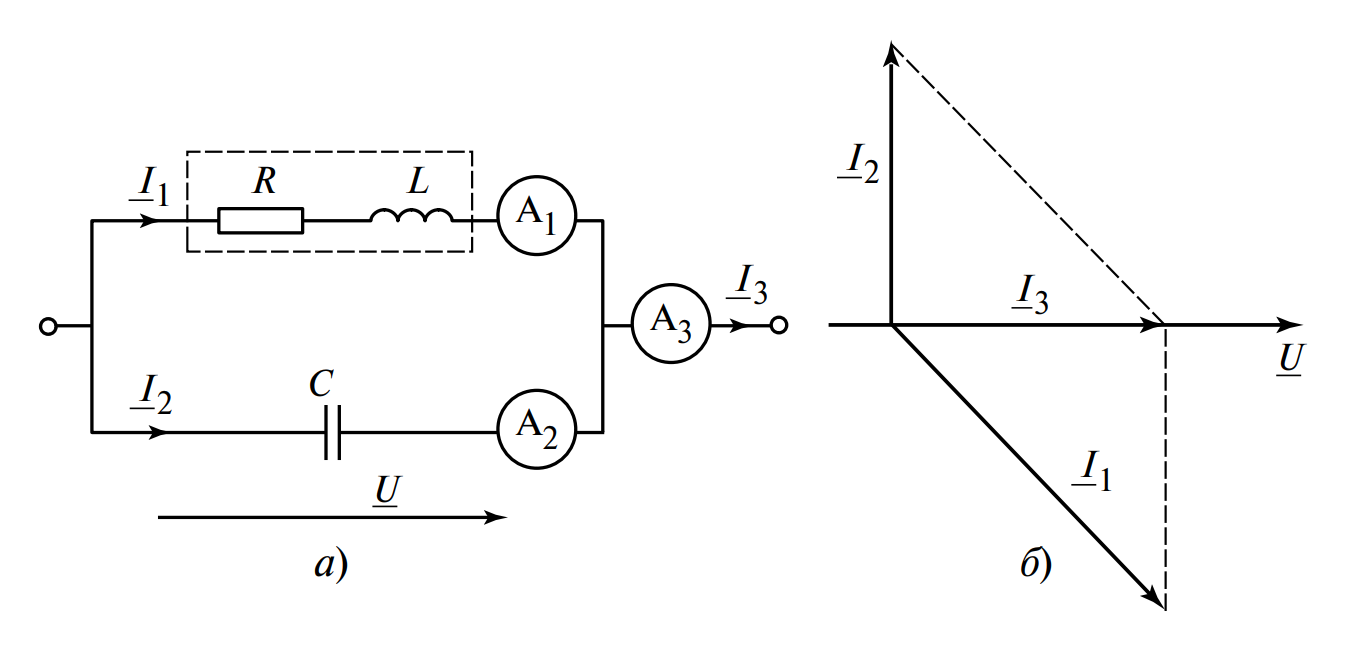
Дано: В цепи, состоящей из параллельно соединенных реактора (катушки с параметрами \( R, L \)) и конденсатора емкостью \( С \) (см. рис. 3, а), известны показания амперметров \( А_2 \) и \( А_3 \):
\( I_2 = I_3 = 1 \) А.
Известно, что имеет место резонанс токов.
Найти: Показание амперметра \( А_1 \) в ветви реактора.

Рис. 3. К примеру: а) схема цепи с амперметрами; б) векторная диаграмма токов.

Решение

Анализ условия резонанса: Так как в цепи резонанс токов, общий входной ток совпадает по фазе с напряжением источника (см. рис. 3, б). Это значит, что входной ток является чисто активным.
Анализ токов: Комплекс тока в емкостном элементе (ветвь с амперметром \( А_2 \)) опережает по фазе напряжение на 90° (так как конденсатор идеальный, \( R_2 \approx 0 \)).
Применение закона Кирхгофа: По первому закону Кирхгофа векторная сумма токов ветвей равна общему току:
\( \vec{I}_{вх} = \vec{I}_1 + \vec{I}_2 \). В нашем случае \( I_3 \) — это общий ток, \( I_2 \) — ток конденсатора, \( I_1 \) — искомый ток реактора.
Геометрический расчет: Из векторной диаграммы следует, что ток реактора \( \vec{I}_1 \) должен компенсировать реактивную составляющую тока конденсатора и обеспечивать активную составляющую общего тока.Так как \( I_3 = 1 \) А (активный ток) и \( I_2 = 1 \) А (чисто емкостный ток), то ток реактора \( I_1 \) будет гипотенузой прямоугольного треугольника с катетами, равными активной и реактивной составляющим.Активная составляющая \( I_1 \) должна быть равна \( I_3 = 1 \) А.
Реактивная (индуктивная) составляющая \( I_1 \) должна компенсировать \( I_2 = 1 \) А.

I_1 = \sqrt{I_{актив}^2 + I_{реактив}^2} = \sqrt{1^2 + 1^2} = \sqrt{2} \approx 1,41 \text{ А}

Ответ: Показание амперметра \( А_1 \) составляет 1,41 А.

Сравнение: Резонанс токов vs Резонанс напряжений

Для более глубокого понимания полезно сравнить параллельный резонанс (токов) с последовательным (напряжений).

Характеристика	Резонанс напряжений (Последовательный)	Резонанс токов (Параллельный)
Схема соединения	R, L, C соединены последовательно	Ветвь L и ветвь C соединены параллельно
Импеданс (Z) при резонансе	Минимален (= R)	Максимален (в идеальном LC контуре стремится к бесконечности)
Ток от источника	Максимален	Минимален
Опасный фактор	Перенапряжение на L и C (может пробить изоляцию)	Большие токи внутри контура (могут перегреть обмотки)
Применение	Входные цепи радиоприемников (для пропускания сигнала)	Заграждающие фильтры, выходные каскады передатчиков

Преимущества и недостатки использования резонанса токов

Преимущества:

Высокое сопротивление на резонансной частоте позволяет использовать контур как качественный фильтр-пробку (заграждающий фильтр) для подавления помех определенной частоты.
Возможность накопления значительной энергии в магнитном и электрическом полях контура.
Увеличение коэффициента мощности (cos φ) цепи до 1 (компенсация реактивной мощности).

Недостатки:

При неправильном расчете большие внутренние токи могут вывести из строя элементы контура (расплавить провода катушки).
Сложность настройки в цепях с изменяющимися параметрами нагрузки.

Интересные факты о резонансе

Индукционный нагрев. Явление резонанса токов используется в индукционных печах для плавки металла, где большие контурные токи разогревают сырье.
Опасность в энергетике. В высоковольтных линиях электропередач резонанс токов может возникнуть самопроизвольно, что является аварийным режимом.
Технологии RFID. RFID-метки в магазинах работают на принципе резонанса: антенна рамки на выходе создает поле, и контур внутри метки резонирует, посылая ответ.
Идеальное сопротивление. Идеальный параллельный контур без потерь (R=0) имел бы бесконечное сопротивление на резонансной частоте.
Суть добротности. Понятие «добротность» (Q-factor) показывает, во сколько раз ток в контуре больше тока источника при резонансе токов.
Природа микроволн. Микроволновые печи используют резонанс молекул воды, но это уже молекулярный резонанс, хотя принцип «накачки» энергии схож с электрическим контуром.
Теория и практика. «Безразличный резонанс» — это теоретический казус, который на практике почти невозможно реализовать идеально из-за паразитных параметров компонентов.

Часто задаваемые вопросы (FAQ)

❓ 1. Почему при резонансе токов общий ток уменьшается?

Потому что индуктивный и емкостный токи находятся в противофазе (сдвинуты на 180 градусов). Катушка «отдает» ток, когда конденсатор его «принимает», и наоборот. Токи циркулируют внутри контура, а от источника требуется только ток для компенсации тепловых потерь на резисторах.

❓ 2. Можно ли получить резонанс, изменяя только сопротивление резистора?

В общей формуле резонансной частоты присутствуют \( R_1 \) и \( R_2 \). Это значит, что изменение активного сопротивления смещает точку резонанса. Однако, если \( R \) слишком велико (превышает \( \rho \)), резонанс может стать невозможным.

❓ 3. Что такое «контур-пробка»?

Это параллельный LC-контур, включенный последовательно с нагрузкой. На резонансной частоте он имеет огромное сопротивление и не пропускает сигнал этой частоты, «затыкая» его проход.

❓ 4. Где применяется резонанс токов в быту?

В блоках питания компьютеров и энергосберегающих лампах (корректоры коэффициента мощности), в радиоприемниках для настройки на станцию, в бесконтактных зарядках для телефонов.

❓ 5. Как влияет емкость C на резонансную частоту?

Частота обратно пропорциональна корню из емкости (\( \omega \sim 1/\sqrt{C} \)). Увеличение емкости в 4 раза снизит резонансную частоту в 2 раза.

Заключение

Резонанс токов — это фундаментальное явление в электротехнике, позволяющее управлять частотными характеристиками цепей. Понимание того, как взаимодействуют индуктивность и емкость в параллельных ветвях, критически важно для инженеров-энергетиков и разработчиков электроники. Грамотное использование этого эффекта лежит в основе работы современной радиосвязи, фильтрации сигналов и систем компенсации реактивной мощности.

Нормативная база

ГОСТ Р 52002-2003 «Электротехника. Термины и определения основных понятий». (Определяет понятия резонанса в электрических цепях).
ГОСТ 19880-74 «Электротехника. Основные понятия. Термины и определения».
ГОСТ IEC 60050-151-2014 «Международный электротехнический словарь. Часть 151. Электрические и магнитные устройства».

Список литературы:

Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Юрайт, 2020.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. — СПб.: Энергоатомиздат, 2009.
Зевеке Г.В., Ионкин П.А. Основы теории цепей. — М.: Энергия, 1989.