Четырехполюсники: теория, параметры и схемы замещения

Содержание страницы

1. Основные уравнения и параметры четырехполюсников
2. Определение коэффициентов четырехполюсников
3. Вторичные параметры четырехполюсников
4. Активные четырехполюсники
Сравнение систем параметров четырехполюсников
Преимущества и недостатки метода
Интересные факты о четырехполюсниках
Часто задаваемые вопросы (FAQ)
Заключение

Что такое четырехполюсник? В теории электрических цепей четырехполюсником называют любую электрическую цепь или ее часть, которая имеет две пары зажимов (два «полюса» на вход и два на выход). Одна пара зажимов, 1-1′, именуется входной, а вторая, 2-2′, — выходной.

Концепция четырехполюсника — это мощный метод «черного ящика». Вместо того чтобы анализировать каждое внутреннее соединение сложной схемы (например, усилителя, фильтра или длинной линии электропередачи), мы описываем ее поведение исключительно через связь между токами и напряжениями на ее входе и выходе. Этот подход значительно упрощает анализ сложных систем.

Краткая история: Развитие теории четырехполюсников началось в конце XIX – начале XX века, во многом благодаря работам по анализу телеграфных и телефонных линий. Ученым требовался способ моделирования затухания и искажения сигнала в длинных кабелях. Это привело к разработке концепций характеристического сопротивления и постоянной передачи, которые и легли в основу теории четырехполюсников, став фундаментальным инструментом в электротехнике, радиотехнике и электронике.

Примечание: Представьте четырехполюсник как музыкальный усилитель. У него есть «вход» (куда вы подключаете гитару) и «выход» (куда вы подключаете колонку). Теория четырехполюсников позволяет нам, не зная точной схемы внутри усилителя, создать математическую модель, которая скажет: «Если на вход подать 1 Вольт, на выходе будет 10 Вольт». Это и есть основная задача данного метода — установить связь между входом и выходом.

Исследование режима работы сложной электрической цепи часто сводится к установлению связи между токами и напряжениями различных ее ветвей. При этом режим остальной части цепи может оставаться неизвестным, хотя все ее параметры учитываются при решении задачи.

В таких условиях рассматриваемая цепь может определяться обобщенными параметрами на соответствующих зажимах, относительно которых параметры заданы или должны быть найдены. Обычно рассматривают цепь относительно входных и выходных зажимов.

Классификация четырехполюсников

Часть электрической цепи, содержащую два входных и два выходных зажима, называют четырехполюсником. На рисунке 1 изображены различные типы четырехполюсников.

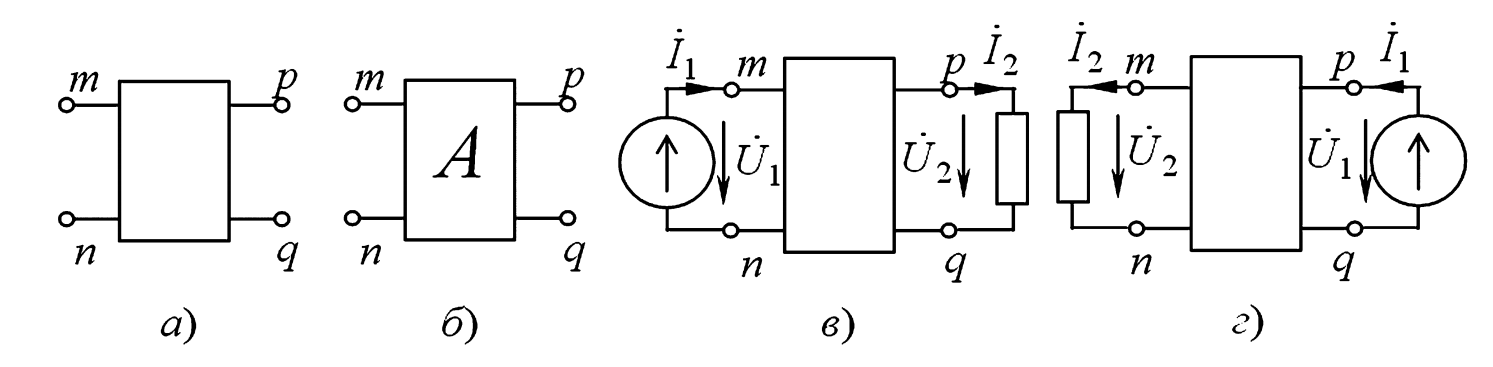
Рисунок 1 — Схемы четырехполюсников:

а — пассивного; б — активного; в — при прямом включении; г — при обратном включении.

- Пассивный четырехполюсник (рис. 1, а) не содержит в своей структуре источников ЭДС или тока. Он может только рассеивать или накапливать энергию (например, фильтры из резисторов, конденсаторов, катушек).
- Активный четырехполюсник (рис. 1, б) содержит во внутренней схеме замещения источники тока или ЭДС (например, усилители на транзисторах или операционных усилителях).

Если на разомкнутых зажимах четырехполюсника (т. е. когда он отключен от внешних источников) обнаруживается напряжение, то такой активный четырехполюсник называется автономным. У неавтономного четырехполюсника внутренняя ЭДС имеет расчетный характер (например, схема замещения транзистора содержит источник тока или источник ЭДС, но если транзистор никуда не подключен, то на его зажимах напряжения не обнаруживается).

Рисунки 1, в и 1, г иллюстрируют прямое (источник на входе 1-1′) и обратное (источник на входе 2-2′) включение.

Схемы замещения пассивных четырехполюсников

При работе пассивного четырехполюсника в качестве связующего звена между источником и нагрузкой предполагается, что могут изменяться нагрузка и напряжение на входе, но схема внутренних соединений и значения сопротивлений остаются неизменными. Поэтому такие четырехполюсники называют проходными.

Схемы замещения проходных пассивных четырехполюсников содержат, как правило, минимальное число элементов (2 или 3). Для уравновешенных схем замещения — 4 или 5 элементов.

На рисунке 2 представлены наиболее распространенные схемы замещения проходных четырехполюсников.

Рисунок 2 — Схемы четырехполюсников:

а — Г-образная, б — П-образная, в — Т-образная, г — П-образная уравновешенная, д — Т-образная уравновешенная, е, ж — мостовые.

Часто вместо базового используют Г-образный четырехполюсник (рис. 2, а). Объединяя два таких четырехполюсника той или иной стороной, получают Т-образные (рис. 2, в) или П-образные (рис. 2, б) симметричные четырехполюсники. При этом чтобы в Т- и П-образных схемах замещения в продольной ветви было сопротивление $Z_1$, необходимо задать в Г-образной схеме замещения в продольной ветви сопротивление $Z_1/2$. Аналогично, чтобы в Т- и П-образных схемах замещения в поперечной ветви было сопротивление $Z_2$, необходимо задать в Г-образной схеме замещения в поперечной ветви сопротивление $2Z_2$.

1. Основные уравнения и параметры четырехполюсников

Для анализа четырехполюсников используются различные системы параметров, связывающие входные и выходные величины. Выбор системы зависит от задачи и способа соединения четырехполюсников.

1.1. А-параметры (параметры передачи)

Между входными и выходными токами и напряжениями (для схемы на рис. 1, в, где ток $\dot{I}_2$ направлен внутрь четырехполюсника) можно установить следующую зависимость:

$$
\begin{cases}
\dot{U}_1 = A \dot{U}_2 + B \dot{I}_2 \\
\dot{I}_1 = C \dot{U}_2 + D \dot{I}_2
\end{cases}
\quad (1)
$$

Уравнения (1) называют основными уравнениями четырехполюсника (в форме A-параметров). Коэффициенты A, B, C, D — это комплексные числа, характеризующие свойства самого четырехполюсника.

Для пассивных и обратимых (reciprocal) четырехполюсников (свойства которых не меняются при смене входа и выхода) коэффициенты связаны соотношением:

$$ AD — BC = 1 \quad (2) $$

Если источник сигнала подключен к зажимам 2-2′ (p и q), а нагрузка — к зажимам 1-1′ (m и n) (рис. 1, г), то уравнения четырехполюсника при обратном включении имеют вид:

$$
\begin{cases}
\dot{U}_2 = D \dot{U}_1 + B \dot{I}_1 \\
\dot{I}_2 = C \dot{U}_1 + A \dot{I}_1
\end{cases}
$$

Если при перемене местами источника и нагрузки токи в источнике и нагрузке не изменяются, то такой четырехполюсник называют симметричным. У него выполняется условие:

$$ A = D $$

Симметричные четырехполюсники (например, симметричные Т- и П-схемы) применяются чаще несимметричных (например, Г-схема).

1.2. Z, Y и h-параметры

Различают также взаимные (обратимые) и невзаимные (необратимые) четырехполюсники. Схемы замещения взаимных четырехполюсников содержат только пассивные R, L, C элементы, а схемы невзаимных — еще и управляемые источники (например, транзисторы).

Наряду с приведенными A-параметрами, применяют еще три варианта уравнений, записанных через Z, Y и h-параметры.

Замечание: При составлении уравнений, записанных через Z, Y и h-параметры, направление тока $\dot{I}_2$ в схеме на рисунке 1, в изменяют на противоположное, т.е. считают его вытекающим из четырехполюсника (положительным для нагрузки).

Z-параметры (параметры сопротивления):

$$
\begin{cases}
\dot{U}_1 = Z_{11} \dot{I}_1 + Z_{12} \dot{I}_2 \\
\dot{U}_2 = Z_{21} \dot{I}_1 + Z_{22} \dot{I}_2
\end{cases}
$$

Y-параметры (параметры проводимости):

$$
\begin{cases}
\dot{I}_1 = Y_{11} \dot{U}_1 + Y_{12} \dot{U}_2 \\
\dot{I}_2 = Y_{21} \dot{U}_1 + Y_{22} \dot{U}_2
\end{cases}
$$

h-параметры (гибридные параметры):

$$
\begin{cases}
\dot{U}_1 = h_{11} \dot{I}_1 + h_{12} \dot{U}_2 \\
\dot{I}_2 = h_{21} \dot{I}_1 + h_{22} \dot{U}_2
\end{cases}
\quad (3)
$$

У симметричных четырехполюсников $Z_{11} = Z_{22}$ и $Y_{11} = Y_{22}$. У обратимых (взаимных) $Z_{12} = Z_{21}$ и $Y_{12} = Y_{21}$.

2. Определение коэффициентов четырехполюсников

Коэффициенты (первичные параметры) A, B, C, D можно определить экспериментально или расчетным путем.

2.1. Экспериментальный метод

При экспериментальном определении коэффициентов используют два классических режима: режим холостого хода (ХХ) и режим короткого замыкания (КЗ). С помощью вольтметра, амперметра и ваттметра (или фазометра) определяют входные сопротивления в этих режимах: $Z_{1xx}$, $Z_{1k}$, $Z_{2k}$ (и $Z_{2xx}$ для несимметричных).

1. Режим холостого хода (XX) на выходе:

Ток $ \dot{I}_2 = 0 $. Уравнения (1) упрощаются:

$\dot{U}_1 = A \dot{U}_2$

$\dot{I}_1 = C \dot{U}_2$

Входное сопротивление $Z_{1xx}$ при холостом ходе на выходе:

$$ Z_{1xx} = \frac{\dot{U}_1}{\dot{I}_1} = \frac{A \dot{U}_2}{C \dot{U}_2} = \frac{A}{C} $$

Коэффициенты A и C можно найти как отношения измеряемых величин:

$A = \dot{U}_{1xx} / \dot{U}_{2xx}$ (коэффициент передачи по напряжению в режиме ХХ)

$C = \dot{I}_{1xx} / \dot{U}_{2xx}$ (имеет размерность проводимости)

2. Режим короткого замыкания (КЗ) на выходе:

Напряжение $ \dot{U}_2 = 0 $. Уравнения (1) упрощаются:

$\dot{U}_1 = B \dot{I}_2$

$\dot{I}_1 = D \dot{I}_2$

Входное сопротивление $Z_{1k}$ при коротком замыкании на выходе:

$$ Z_{1k} = \frac{\dot{U}_1}{\dot{I}_1} = \frac{B \dot{I}_2}{D \dot{I}_2} = \frac{B}{D} $$

Коэффициенты B и D можно найти как:

$B = \dot{U}_{1k} / \dot{I}_{2k}$ (имеет размерность сопротивления)

$D = \dot{I}_{1k} / \dot{I}_{2k}$ (коэффициент передачи по току в режиме КЗ)

Дополняя эти зависимости уравнением $AD — BC = 1$, можно полностью определить все четыре коэффициента. Например, для симметричных четырехполюсников ($A = D$) имеем $Z_{1k} = Z_{2k}$ и $Z_{1xx} = Z_{2xx}$. Тогда:

$A = D = \sqrt{Z_{1xx} / (Z_{1xx} — Z_{1k})}$ (формула не всегда удобна)

Более практичный подход — использовать вторичные параметры (см. раздел 3).

2.2. Расчетный метод

Расчетный метод применяют тогда, когда известна его схема, и она достаточно проста. Этот метод также использует режимы ХХ и КЗ, но уже в аналитическом виде.

Пример 1. Определение коэффициентов Т-образной схемы

Задача: Для схемы, представленной на рисунке 3, а, определить коэффициенты A, B, C, D четырехполюсника.

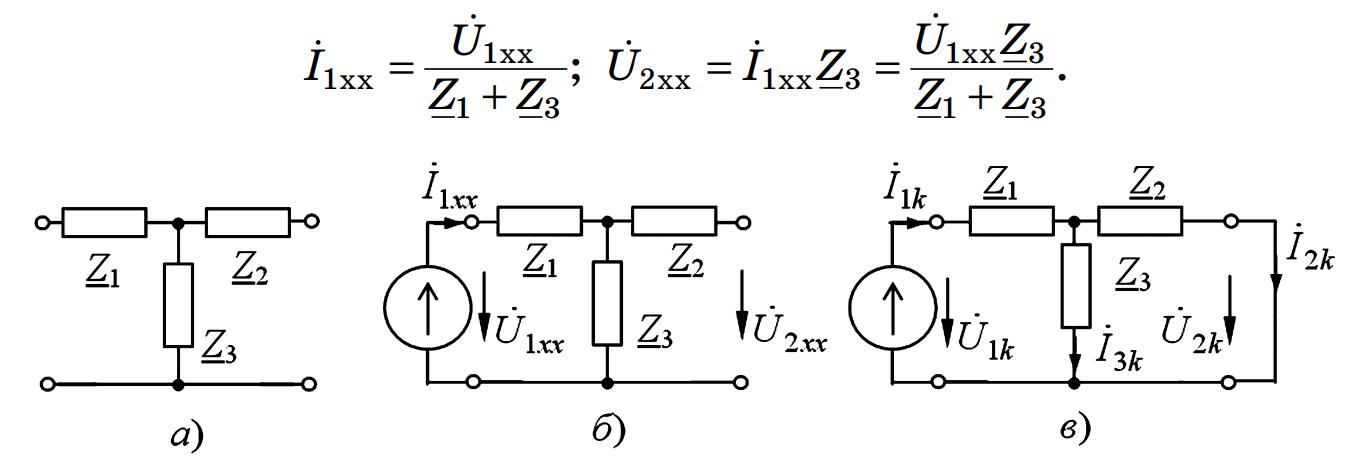
Рисунок 3 — К примеру 1:

а — схема четырехполюсника (Т-схема); б — режим холостого хода; в — режим короткого замыкания.

Решение:

1. Рассматриваем режим холостого хода (рис. 3, б), когда выходные зажимы четырехполюсника разомкнуты ($\dot{I}_2 = 0$), а к входным зажимам подключен источник напряжения $\dot{U}_1$.

Входной ток $\dot{I}_{1xx}$ проходит через $Z_1$ и $Z_3$. Входное сопротивление:

$Z_{1xx} = Z_1 + Z_3$

Входное напряжение: $\dot{U}_{1xx} = \dot{I}_{1xx} Z_{1xx} = \dot{I}_{1xx} (Z_1 + Z_3)$

Напряжение на выходе $\dot{U}_{2xx}$ (напряжение на $Z_3$):

$\dot{U}_{2xx} = \dot{I}_{1xx} Z_3$

2. Используя определенные значения $\dot{I}_{1xx}$ и $\dot{U}_{2xx}$, рассчитываем коэффициенты A и C:

$$ A = \frac{\dot{U}_{1xx}}{\dot{U}_{2xx}} = \frac{\dot{I}_{1xx} (Z_1 + Z_3)}{\dot{I}_{1xx} Z_3} = \frac{Z_1 + Z_3}{Z_3} = 1 + \frac{Z_1}{Z_3} $$
$$ C = \frac{\dot{I}_{1xx}}{\dot{U}_{2xx}} = \frac{\dot{I}_{1xx}}{\dot{I}_{1xx} Z_3} = \frac{1}{Z_3} $$

3. Рассматриваем режим короткого замыкания (рис. 3, в), когда выходные зажимы замкнуты и напряжение $\dot{U}_{2k} = 0$.

Входной ток $\dot{I}_{1k}$ разветвляется на $\dot{I}_2$ (через $Z_2$) и ток через $Z_3$. Общее входное сопротивление $Z_{1k}$ — это $Z_1$ последовательно с параллельным соединением $Z_2$ и $Z_3$:

$Z_{1k} = Z_1 + \frac{Z_2 Z_3}{Z_2 + Z_3} = \frac{Z_1 Z_2 + Z_1 Z_3 + Z_2 Z_3}{Z_2 + Z_3}$

Входное напряжение: $\dot{U}_{1k} = \dot{I}_{1k} Z_{1k}$

Ток $\dot{I}_{2k}$ (с направлением «внутрь» четырехполюсника) найдем по правилу делителя тока (со знаком «плюс», т.к. $\dot{I}_{1k}$ делится):

$\dot{I}_{2k} = \dot{I}_{1k} \frac{Z_3}{Z_2 + Z_3}$

4. Затем рассчитываем коэффициенты B и D:

$$ B = \frac{\dot{U}_{1k}}{\dot{I}_{2k}} = \frac{\dot{I}_{1k} Z_{1k}}{\dot{I}_{1k} \frac{Z_3}{Z_2 + Z_3}} = Z_{1k} \frac{Z_2 + Z_3}{Z_3} = \left( \frac{Z_1 Z_2 + Z_1 Z_3 + Z_2 Z_3}{Z_2 + Z_3} \right) \left( \frac{Z_2 + Z_3}{Z_3} \right) = \frac{Z_1 Z_2 + Z_1 Z_3 + Z_2 Z_3}{Z_3} $$
$$ B = Z_1 + Z_2 + \frac{Z_1 Z_2}{Z_3} $$
$$ D = \frac{\dot{I}_{1k}}{\dot{I}_{2k}} = \frac{\dot{I}_{1k}}{\dot{I}_{1k} \frac{Z_3}{Z_2 + Z_3}} = \frac{Z_2 + Z_3}{Z_3} = 1 + \frac{Z_2}{Z_3} $$

(Проверка: для симметричной Т-схемы $Z_1 = Z_2$, тогда $A = D$, что и наблюдается).

3. Вторичные параметры четырехполюсников

В качестве вторичных параметров четырехполюсников используют характеристические сопротивления $Z_{C1}$, $Z_{C2}$ и постоянную передачи $g$.

Для симметричного четырехполюсника ($A = D$) $Z_{C1} = Z_{C2} = Z_C$.

Характеристическое сопротивление $Z_C$ равно такому сопротивлению нагрузки $Z_н = Z_C$, при котором входное сопротивление четырехполюсника также равно этому сопротивлению $Z_{вх} = Z_C$.

Режим работы, при котором сопротивление нагрузки равно характеристическому сопротивлению четырехполюсника, называют согласованным режимом. В большинстве практических задач (линии связи, ВЧ-устройства) он является желательным, т.к. обеспечивает передачу максимальной мощности и отсутствие отражений сигнала.

Так как у симметричного четырехполюсника $A = D$ и

$$ Z_{вх} = \frac{\dot{U}_1}{\dot{I}_1} = \frac{A \dot{U}_2 + B \dot{I}_2}{C \dot{U}_2 + D \dot{I}_2} = \frac{A (\dot{I}_2 Z_н) + B \dot{I}_2}{C (\dot{I}_2 Z_н) + A \dot{I}_2} = \frac{A Z_н + B}{C Z_н + A} $$

то, подставляя $Z_{вх} = Z_C$ и $Z_н = Z_C$, получим:

$Z_C = (A Z_C + B) / (C Z_C + A)$ $\implies$ $Z_C (C Z_C + A) = A Z_C + B$

$C Z_C^2 + A Z_C = A Z_C + B$ $\implies$ $C Z_C^2 = B$

$$ Z_C = \sqrt{\frac{B}{C}} $$

Для несимметричного четырехполюсника характеристическое сопротивление со стороны входа $Z_{C1}$ связано с таким сопротивлением нагрузки, равном сопротивлению $Z_{C2}$, при котором входное сопротивление равно $Z_{C1}$. Для $Z_{C2}$ сопротивления связаны аналогично.

Практически их находят через опыты ХХ и КЗ:

$$ Z_{C1} = \sqrt{Z_{1xx} Z_{1k}} \quad \text{и} \quad Z_{C2} = \sqrt{Z_{2xx} Z_{2k}} $$

(Примечание: в тексте примера `Z_{C1} = \sqrt{AB/CD}` и `Z_{C2} = \sqrt{BD/AC}` являются следствием Z-параметров, но формулы через ХХ/КЗ более практичны).

Постоянная передачи (g)

Постоянная передачи $g$ является комплексным числом $g = a + jb$, которое показывает, как изменяется комплексная амплитуда сигнала при прохождении через четырехполюсник в согласованном режиме.

$$ \frac{\dot{U}_1}{\dot{U}_2} = \frac{\dot{I}_1}{\dot{I}_2} = e^g = e^{a+jb} = e^a \cdot e^{jb} $$

$a = \ln(U_1 / U_2)$ — коэффициент затухания. Измеряется в Неперах (Нп).
$b = \phi_1 — \phi_2$ — коэффициент фазы (фазовый сдвиг). Измеряется в радианах (рад).

Затуханию в 1 Нп соответствует отношение напряжений $U_1 / U_2 = e^1 \approx 2.718$. На практике чаще используют децибелы (дБ):

$$ a \text{ (дБ)} = 20 \lg \left( \frac{U_1}{U_2} \right) $$

Соотношение: 1 Нп $\approx$ 8.686 дБ.

Постоянная передачи симметричного четырехполюсника может быть определена через А-параметры. В согласованном режиме $\dot{U}_2 = \dot{I}_2 Z_C$:

$\dot{U}_1 = A \dot{U}_2 + B \dot{I}_2 = A \dot{U}_2 + B (\dot{U}_2 / Z_C) = \dot{U}_2 (A + B/Z_C)$

$e^g = \dot{U}_1 / \dot{U}_2 = A + B/Z_C$

Подставляя $Z_C = \sqrt{B/C}$ и $AD-BC=1$ (при $A=D$), $A^2-BC=1$, получаем:

$$ e^g = A + \sqrt{BC} = A + \sqrt{A^2 — 1} $$

Отсюда следует важное соотношение:

$$ A = \frac{e^g + e^{-g}}{2} = \cosh(g) $$

Зная $A = \cosh(g)$ и $Z_C = \sqrt{B/C}$, можно определить все A-параметры через вторичные:

$A = D = \cosh(g)$
$B = Z_C \sinh(g)$
$C = (1 / Z_C) \sinh(g)$

При этом уравнения симметричного четырехполюсника через вторичные параметры имеют вид:

$$
\begin{cases}
\dot{U}_1 = \dot{U}_2 \cosh(g) + \dot{I}_2 Z_C \sinh(g) \\
\dot{I}_1 = \dot{U}_2 (1/Z_C) \sinh(g) + \dot{I}_2 \cosh(g)
\end{cases}
\quad (4)
$$

Входное сопротивление симметричного четырехполюсника при произвольной нагрузке $Z_н$:

$$ Z_{вх} = \frac{\dot{U}_1}{\dot{I}_1} = Z_C \frac{Z_н \cosh(g) + Z_C \sinh(g)}{Z_н \sinh(g) + Z_C \cosh(g)} = Z_C \frac{Z_н + Z_C \tanh(g)}{Z_н \tanh(g) + Z_C} $$

Из этой формулы легко получить сопротивления в режимах КЗ и ХХ:

При коротком замыкании ($Z_н = 0$): $Z_k = Z_C \tanh(g)$
При холостом ходе ($Z_н \to \infty$): $Z_{xx} = Z_C / \tanh(g)$

Перемножив эти два выражения, получаем практический способ определения $Z_C$ и $g$:

$$ Z_C = \sqrt{Z_{xx} Z_k} \quad \text{и} \quad \tanh(g) = \sqrt{\frac{Z_k}{Z_{xx}}} \quad (5) $$

Таким образом, измерив экспериментально $Z_{xx}$ и $Z_k$, можно определить оба вторичных параметра.

Пример 2. Каскадное соединение

Задача: Три симметричных четырехполюсника, имеющие одинаковые параметры $Z_C$ и $g$, соединены каскадно (последовательно один за другим). Определить входное сопротивление и постоянную передачи каскада, если сопротивление нагрузки $Z_н = Z_C$.

Рисунок 4 — Схема к примеру 2

Решение:

1. Учитывая, что входное сопротивление четырехполюсника при согласованном режиме включения (т. е. при $Z_н = Z_C$) также равно $Z_{вх} = Z_C$, получим, что все три четырехполюсника оказались включенными в согласованном режиме. Нагрузкой для третьего 4П является $Z_C$, значит его входное сопротивление $Z_C$. Это сопротивление является нагрузкой для второго 4П, и т.д.

Входное сопротивление всего каскада равно $Z_{вх.общ} = Z_C$.

2. Так как выходное напряжение $\dot{U}_2$ первого каскада является входным напряжением второго каскада (рис. 4), т. е. $\dot{U}_2 = \dot{U}_1’$ и аналогично $\dot{U}_2′ = \dot{U}_1»$, то:

$\dot{U}_1 / \dot{U}_2 = e^g$

$\dot{U}_1′ / \dot{U}_2′ = e^g \implies \dot{U}_2 / \dot{U}_2′ = e^g$

$\dot{U}_1» / \dot{U}_2» = e^g \implies \dot{U}_2′ / \dot{U}_2» = e^g$

Общее отношение $\dot{U}_1 / \dot{U}_2»$:

$$ \frac{\dot{U}_1}{\dot{U}_2»} = \frac{\dot{U}_1}{\dot{U}_2} \cdot \frac{\dot{U}_2}{\dot{U}_2′} \cdot \frac{\dot{U}_2′}{\dot{U}_2»} = e^g \cdot e^g \cdot e^g = e^{3g} $$

Общая постоянная передачи каскада: $g_{общ} = g + g + g = 3g$.

Вывод: При каскадном соединении согласованных четырехполюсников их постоянные передачи (и затухания в Неперах/дБ) складываются.

4. Активные четырехполюсники

В автоматике, связи, информатике, радиоэлектронике применяют электрические схемы, выполняющие функции усилителей, генераторов, а также более сложных устройств, таких как отрицательные резисторы, имитаторы индуктивности, частотно-зависимые элементы и т.д. Реализуют эти элементы обычно с помощью схем с операционными усилителями (ОУ).

Для анализа различных схем и моделирования на ЭВМ оказалось целесообразным ввести в качестве базисных элементов наряду с двухполюсниками R, L, C зависимые (управляемые) источники — такие четырехполюсники, у которых значение выходной функции (представляющей источник тока или ЭДС) зависит от входного напряжения или тока.

4.1. Зависимые источники

Наряду с двухполюсными идеализированными элементами (источниками тока и ЭДС), применяют четырехполюсные идеализированные элементы — зависимые источники. Для четырех возможных сочетаний входной и выходной величин вводят четыре типа зависимых источников.

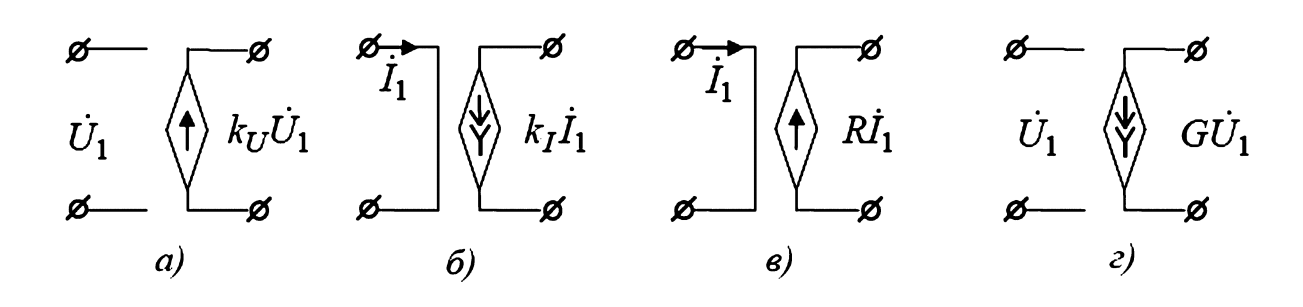
Рисунок 5 — Зависимые источники:

а — ИНУН; б — ИТУТ; в — ИНУТ; г — ИТУН.

Зависимый источник напряжения, управляемый напряжением (ИНУН) (рис. 5, а). Идеализация усилителя напряжения.Уравнения: $\dot{I}_1 = 0$; $\dot{U}_2 = k_U \dot{U}_1$.Входное сопротивление бесконечно велико.
Зависимый источник тока, управляемый током (ИТУТ) (рис. 5, б). Идеализация усилителя тока.Уравнения: $\dot{U}_1 = 0$; $\dot{I}_2 = k_I \dot{I}_1$.Входное сопротивление равно нулю.
Зависимый источник напряжения, управляемый током (ИНУТ) (рис. 5, в).Уравнения: $\dot{U}_1 = 0$; $\dot{U}_2 = R \dot{I}_1$.Входное сопротивление равно нулю.
Зависимый источник тока, управляемый напряжением (ИТУН) (рис. 5, г).Уравнения: $\dot{I}_1 = 0$; $\dot{I}_2 = G \dot{U}_1$.Входное сопротивление бесконечно велико.

Уравнения зависимых источников можно записать в матричной форме. Например, для ИНУН (через h-параметры, но с $\dot{I}_2$ как выходной функцией) или для ИТУН (через Y-параметры):

Матрица Y для ИТУН: $ [Y] = \begin{bmatrix} 0 & 0 \\ G & 0 \end{bmatrix} $

4.2. Операционный усилитель (ОУ)

Идеальный операционный усилитель (ОУ) представляет собой ИНУН с бесконечно большим коэффициентом усиления ($k_U \to \infty$) и бесконечно большим входным сопротивлением. Выходное сопротивление считается нулевым.

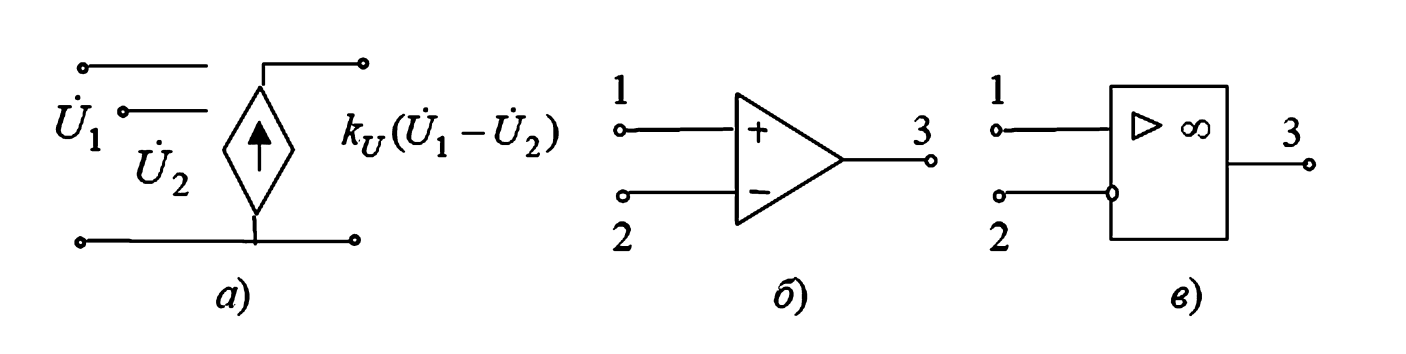
Рисунок 6 — Обозначения ОУ:

а — как ИНУН; б — как элемент в теории цепей; в — как в электрических схемах (по ГОСТ).

Третий вариант (рис. 6, в) используется по ГОСТ 2.721-74 (ЕСКД. Обозначения условные графические в схемах. Общие положения) для изображения реальной микросхемы на принципиальных электрических схемах.

У ОУ имеется два входа — инвертирующий (обозначается «-«) и неинвертирующий (обозначается «+»). Полярность напряжения инвертирующего входа обратна полярности напряжения на выходе ОУ, а у неинвертирующего входа — одинакова.

Так как коэффициент усиления ОУ $k_U \to \infty$, то для конечного выходного напряжения разность входных напряжений $\dot{U}_+ — \dot{U}_-$ стремится к нулю. Это «виртуальное» равенство потенциалов — ключ к анализу схем на ОУ.

На рисунке 7, а представлена простейшая схема инвертирующего усилителя.

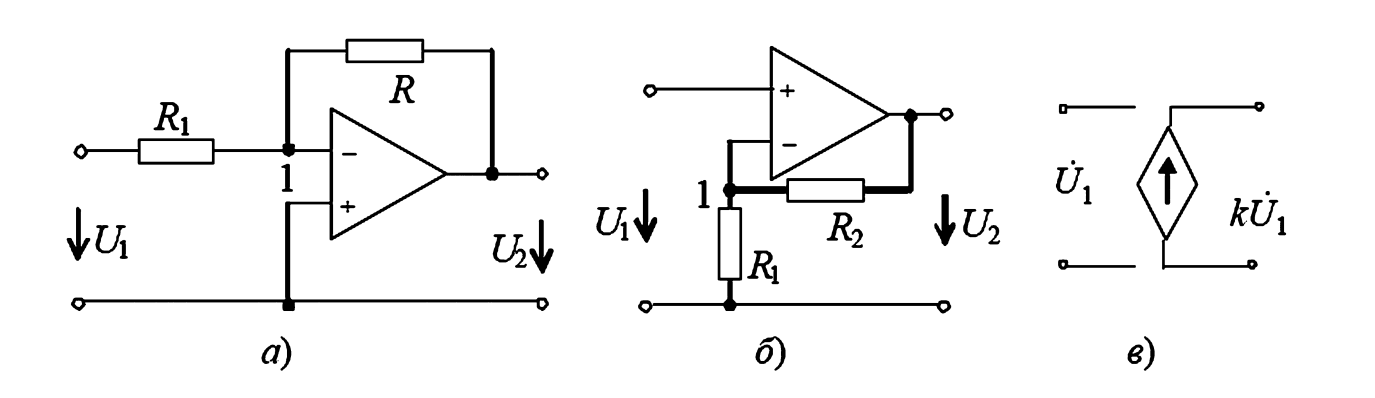
Рисунок 7 — Схемы усилителей:

а — инвертирующего; б — неинвертирующего; в — ИНУН.

Анализ инвертирующего усилителя (рис. 7, а):

Так как неинвертирующий вход («+») заземлен ($\dot{U}_+ = 0$), то из-за $k_U \to \infty$, потенциал инвертирующего входа («-«) также равен нулю ($\dot{U}_- \approx 0$, «виртуальная земля»). Входной ток ОУ равен нулю ($I_{вх} = 0$), поэтому ток через $R_1$ равен току через $R_2$. По 1-му закону Кирхгофа для узла 1 (инвертирующий вход):

$\dot{I}_1 + \dot{I}_2 = 0$

$\frac{\dot{U}_1 — \dot{U}_-}{R_1} + \frac{\dot{U}_2 — \dot{U}_-}{R_2} = 0$

Подставляя $\dot{U}_- = 0$, получаем:

$\frac{\dot{U}_1}{R_1} + \frac{\dot{U}_2}{R_2} = 0$

$$ \frac{\dot{U}_2}{\dot{U}_1} = — \frac{R_2}{R_1} $$

Выходное напряжение $\dot{U}_2$ находится в противофазе со входным $\dot{U}_1$.

Анализ неинвертирующего усилителя (рис. 7, б):

Здесь $\dot{U}_+ = \dot{U}_1$. Из-за $k_U \to \infty$, $\dot{U}_- \approx \dot{U}_+ = \dot{U}_1$. Ток в ОУ не течет. Сумма токов в узле 1 (инвертирующий вход):

$\frac{0 — \dot{U}_-}{R_1} + \frac{\dot{U}_2 — \dot{U}_-}{R_2} = 0$

Подставляя $\dot{U}_- = \dot{U}_1$:

$\frac{-\dot{U}_1}{R_1} + \frac{\dot{U}_2 — \dot{U}_1}{R_2} = 0 \implies \frac{\dot{U}_2}{R_2} = \frac{\dot{U}_1}{R_1} + \frac{\dot{U}_1}{R_2} = \dot{U}_1 \left( \frac{R_1 + R_2}{R_1 R_2} \right) $

$$ \frac{\dot{U}_2}{\dot{U}_1} = R_2 \left( \frac{R_1 + R_2}{R_1 R_2} \right) = \frac{R_1 + R_2}{R_1} = 1 + \frac{R_2}{R_1} $$

Выходное напряжение $\dot{U}_2$ синфазно со входным $\dot{U}_1$.

При расчетах обе эти схемы могут быть представлены как ИНУН (рис. 7, в) с $k = -R_2/R_1$ или $k = 1 + R_2/R_1$.

4.3. Конвертор и инвертор сопротивлений

С помощью ОУ можно получить активные четырехполюсники, которые преобразуют комплексное сопротивление, присоединенное на выходе.

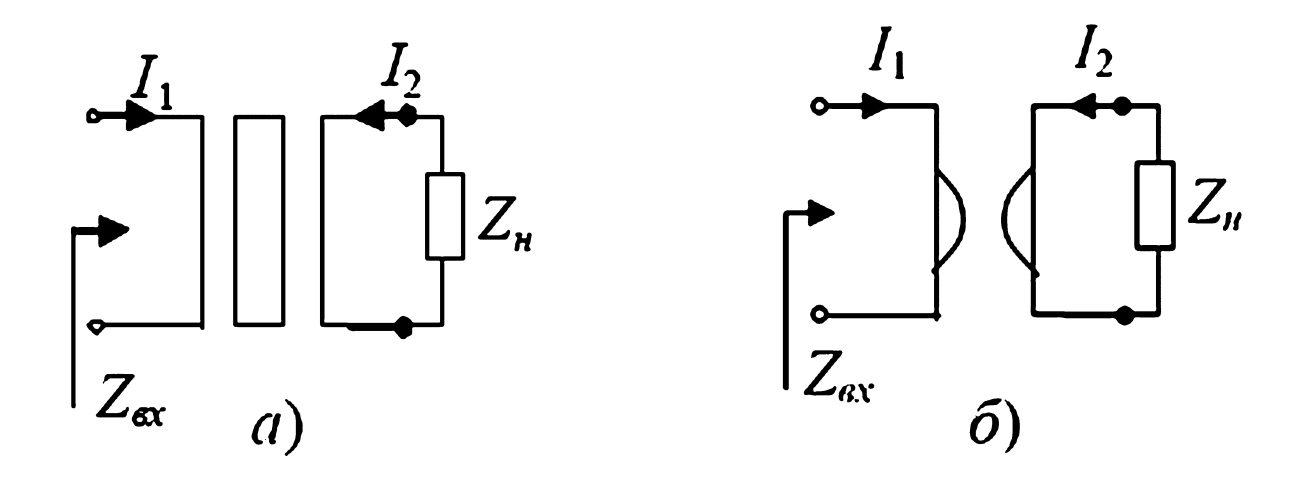
Обозначение преобразователей сопротивлений — конвертор и инвертор

Рисунок 8 — Обозначение преобразователей сопротивлений:

а — конвертор; б — инвертор.

А. Конвертор сопротивления (рис. 8, а)

Четырехполюсник, у которого первичные параметры $B = 0$ и $C = 0$, позволяет изменять значение сопротивления. У него:

$$ Z_{вх} = \frac{A Z_н + B}{C Z_н + D} = \frac{A Z_н}{D Z_н} = \left( \frac{A}{D} \right) Z_н = k Z_н $$

Если A и D имеют одинаковые знаки, это конвертор положительного сопротивления (похож на идеальный трансформатор). Если знаки разные — конвертор отрицательного сопротивления (НИК – Негативный Импедансный Конвертер). Отрицательные сопротивления используются для создания генераторов и компенсации потерь.

Б. Инвертор сопротивлений (рис. 8, б)

Четырехполюсник, у которого $A = 0$ и $D = 0$, является инвертором сопротивлений. У него:

$$ Z_{вх} = \frac{A Z_н + B}{C Z_н + D} = \frac{B}{C Z_н} = \frac{k}{Z_н} $$

Входное сопротивление обратно пропорционально сопротивлению нагрузки.

Частный случай инвертора — гиратор. С помощью гиратора и емкости можно имитировать индуктивность. Это имеет огромное практическое значение в микроэлектронике.

Действительно, при $Z_н = Z_C = 1 / (j \omega C)$:

$$ Z_{вх} = \frac{k}{Z_н} = \frac{k}{1 / (j \omega C)} = j \omega (k C) = j \omega L_{экв} $$

Входное сопротивление такой схемы эквивалентно индуктивности $L_{экв} = kC$.

Это позволяет создавать фильтры и колебательные контуры в интегральных микросхемах, где изготовление физических катушек индуктивности больших номиналов технологически невозможно или очень дорого.

Каскадное соединение двух гираторов эквивалентно идеальному трансформатору.

Сравнение систем параметров четырехполюсников

Выбор системы параметров (A, Z, Y, h) диктуется удобством анализа конкретной схемы.

Тип параметров	Независимые переменные	Зависимые переменные	Определяющие уравнения	Основное применение
A (Передачи)	$\dot{U}_2, \dot{I}_2$ (Выход)	$\dot{U}_1, \dot{I}_1$ (Вход)	$\dot{U}_1 = A\dot{U}_2 + B\dot{I}_2$ $\dot{I}_1 = C\dot{U}_2 + D\dot{I}_2$	Анализ каскадных соединений (матрицы A перемножаются), линии передачи.
Z (Сопротивления)	$\dot{I}_1, \dot{I}_2$ (Токи)	$\dot{U}_1, \dot{U}_2$ (Напряжения)	$\dot{U}_1 = Z_{11}\dot{I}_1 + Z_{12}\dot{I}_2$ $\dot{U}_2 = Z_{21}\dot{I}_1 + Z_{22}\dot{I}_2$	Анализ последовательного соединения четырехполюсников (матрицы Z складываются).
Y (Проводимости)	$\dot{U}_1, \dot{U}_2$ (Напряжения)	$\dot{I}_1, \dot{I}_2$ (Токи)	$\dot{I}_1 = Y_{11}\dot{U}_1 + Y_{12}\dot{U}_2$ $\dot{I}_2 = Y_{21}\dot{U}_1 + Y_{22}\dot{U}_2$	Анализ параллельного соединения четырехполюсников (матрицы Y складываются).
h (Гибридные)	$\dot{I}_1, \dot{U}_2$ (Смешанные)	$\dot{U}_1, \dot{I}_2$ (Смешанные)	$\dot{U}_1 = h_{11}\dot{I}_1 + h_{12}\dot{U}_2$ $\dot{I}_2 = h_{21}\dot{I}_1 + h_{22}\dot{U}_2$	Моделирование электронных компонентов, особенно биполярных транзисторов (BJT).

Преимущества и недостатки метода

Преимущества

Модульность: Позволяет анализировать очень сложные системы, разбивая их на простые, стандартно описанные блоки.
Упрощение: Скрывает ненужную внутреннюю детализацию, фокусируясь только на поведении «вход-выход».
Универсальность: Метод применим не только к электрическим цепям, но и к акустическим, механическим и оптическим системам, где есть вход и выход.
Стандартизация: Позволяет легко комбинировать компоненты (например, при каскадном соединении A-матрицы просто перемножаются).

Недостатки

Линейность: Классическая теория четырехполюсников применима только для линейных цепей (где $U$ пропорционально $I$). Она не работает для нелинейных компонентов при больших сигналах.
«Черный ящик»: Метод не дает информации о физических процессах, протекающих внутри устройства, или о его энергопотреблении (если это не активный 4П).
Ограничения по частоте: Параметры (A, Z, Y, h) являются частотно-зависимыми. Модель, рассчитанная для 1 кГц, будет неверной для 1 ГГц.

Интересные факты о четырехполюсниках

Телефонные линии как 4П: Теория четырехполюсников во многом была разработана для моделирования тысяч километров телефонных и телеграфных линий, позволяя рассчитать затухание сигнала и необходимость в усилителях.
Матрицы — это удобно: При каскадном соединении (усилитель -> фильтр -> линия) общая A-матрица системы равна произведению A-матриц каждого блока: $[A]_{общ} = [A]_1 \cdot [A]_2 \cdot [A]_3$.
Идеальный трансформатор — это 4П: Идеальный трансформатор с коэффициентом $n$ — это конвертор сопротивления, у которого $A=n$, $D=1/n$, а $B=0$ и $C=0$.
«Невозможная» индуктивность: Гираторы (активные 4П) позволяют создавать в микросхемах «синтетические» катушки индуктивности, используя только транзисторы и конденсаторы.
Создание колебаний: Активные четырехполюсники с отрицательным сопротивлением (НИК) являются ключевым элементом во многих генераторах (осцилляторах), так как они компенсируют потери в колебательном контуре, «подкачивая» в него энергию.

Часто задаваемые вопросы (FAQ)

1. В чем разница между симметричным и обратимым (взаимным) четырехполюсником?

Это разные свойства. Симметричный — это «геометрическое» свойство. Он выглядит одинаково со стороны входа и выхода (например, Т-схема с $Z_1=Z_2$). У него $A=D$. Обратимый (взаимный) — это «физическое» свойство. Он не содержит управляемых источников (транзисторов, ОУ). Если поменять местами идеальный источник ЭДС и амперметр, показания амперметра не изменятся. У него $AD-BC=1$ (для пассивных) или $Z_{12}=Z_{21}$. Пассивный симметричный 4П всегда обратим, но обратимый не всегда симметричен (например, Г-схема).

2. Зачем менять направление тока I₂ для Z, Y и h-параметров?

Это вопрос соглашения. A-параметры (параметры передачи) удобны, когда мы «следим» за сигналом слева направо, поэтому $\dot{I}_1$ и $\dot{I}_2$ направляют в одну сторону (например, внутрь 4П). Z, Y, h-параметры (параметры цепи) удобнее, когда 4П рассматривается как «элемент» схемы. Для любого элемента (как резистор) принято, что ток, втекающий в зажим, является положительным. Поэтому $\dot{I}_1$ и $\dot{I}_2$ направляют внутрь четырехполюсника (или $\dot{I}_2$ направляют наружу, в нагрузку, что меняет знак в уравнениях). Важно всегда проверять условное направление токов в используемой литературе.

3. Что такое «согласованная нагрузка» и почему она важна?

Согласованная нагрузка — это когда сопротивление нагрузки $Z_н$ равно характеристическому сопротивлению $Z_C$ четырехполюсника (или линии передачи). Это критически важно по двум причинам: 1) Максимальная передача мощности: При $Z_н = Z_C$ в нагрузку от источника передается максимальная мощность. 2) Отсутствие отражений: В высокочастотных цепях (ТВ-кабель, Ethernet) несогласованность приводит к отражению сигнала от конца линии обратно к источнику, что вызывает искажения («двоение» изображения, ошибки данных).

4. Можно ли использовать теорию четырехполюсников для цепей постоянного тока (DC)?

Да, абсолютно. В этом случае все комплексные сопротивления (импедансы $Z$) становятся активными сопротивлениями ($R$). Катушки индуктивности ($Z_L = j\omega L$) становятся коротким замыканием ($R=0$), а конденсаторы ($Z_C = 1 / (j\omega C)$) — разрывом цепи ($R \to \infty$). Все уравнения (1)-(5) остаются справедливыми, просто все коэффициенты (A, B, C, D) становятся вещественными числами.

5. Что такое Непер (Нп) и почему он используется вместо децибел (дБ)?

И Непер, и децибел — это логарифмические единицы для измерения затухания или усиления. Непер (Нп) основан на натуральном логарифме (ln) и естественно возникает в уравнениях линий передачи (как $e^g$). Затухание в 1 Нп означает, что напряжение уменьшилось в $e^1 \approx 2.718$ раз. Децибел (дБ) основан на десятичном логарифме (lg) и исторически более популярен в акустике и радиотехнике. $a \text{ (дБ)} = 20 \lg(U_1/U_2)$. Обе единицы равноправны, 1 Нп $\approx$ 8.686 дБ.

Заключение

Теория четырехполюсников — это краеугольный камень современного анализа электрических цепей. Она предоставляет инженерам и студентам мощный и гибкий математический аппарат для «декомпозиции» сложных систем — от пассивных фильтров и линий электропередачи до сложных активных схем на операционных усилителях.

Понимание A, Z, Y, h-параметров, а также вторичных характеристик ($Z_C$ и $g$), позволяет не просто рассчитывать токи и напряжения, но и проектировать системы с заданными свойствами: нужным усилением, требуемой полосой пропускания и согласованием для максимальной эффективности. От анализа простой Т-схемы до синтеза индуктивности на гираторе — метод четырехполюсников остается универсальным и незаменимым инструментом в арсенале специалиста по электронике и электротехнике.

Нормативные документы

ГОСТ Р 52002-2003 — Электротехника. Термины и определения основных понятий. (Устанавливает основную терминологию, включая «четырехполюсник»).
ГОСТ 2.721-74 — Единая система конструкторской документации (ЕСКД). Обозначения условные графические в схемах. Общие положения. (Регламентирует графическое обозначение элементов, включая операционные усилители).

Четырехполюсники: уравнения, параметры (A, Z, Y, h) и схемы замещения