Расчет цепей с взаимной индуктивностью

Содержание страницы

Магнитные потоки и определение взаимной индуктивности
Разметка катушек и экспериментальное определение M
Расчет разветвленных цепей с взаимными индуктивностями
Метод устранения индуктивных связей («Развязка»)
Трансформатор без ферромагнитного сердечника (Воздушный)
Преимущества и недостатки индуктивной связи
Сравнение согласного и встречного включения
Интересные факты о взаимной индуктивности
FAQ: Часто задаваемые вопросы
Заключение

Основой для понимания взаимной индукции служит закон электромагнитной индукции Фарадея. В то время как самоиндукция описывает ЭДС, возникающую в контуре при изменении тока в этом же контуре, взаимная индукция расширяет этот принцип на несколько контуров. Это явление, при котором изменение тока в одном элементе цепи (например, в катушке) приводит к появлению электродвижущей силы (ЭДС) в другом, гальванически не связанном с ним элементе.

Если два таких элемента расположены достаточно близко, их магнитные поля взаимодействуют. Считают, что эти два элемента индуктивно связаны, а возникающую ЭДС называют ЭДС взаимной индукции. Это явление было независимо открыто Майклом Фарадеем в Англии (1831 г.) и Джозефом Генри в США (1832 г.). Оно лежит в основе работы трансформаторов, беспроводной передачи энергии, индукционных плит и многих других устройств.

Магнитные потоки и определение взаимной индуктивности

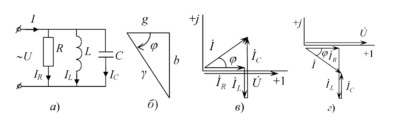
На рисунке 1а схематично представлено распределение магнитных потоков у двух близко расположенных индуктивных катушек. У магнитного потока первой катушки $\Phi_1$ часть потока $\Phi_{11}$ связана (сцеплена) только с витками этой катушки (поток рассеяния), а часть потока $\Phi_{12}$ пронизывает вторую катушку (взаимный поток), т. е. $\Phi_1 = \Phi_{11} + \Phi_{12}$.

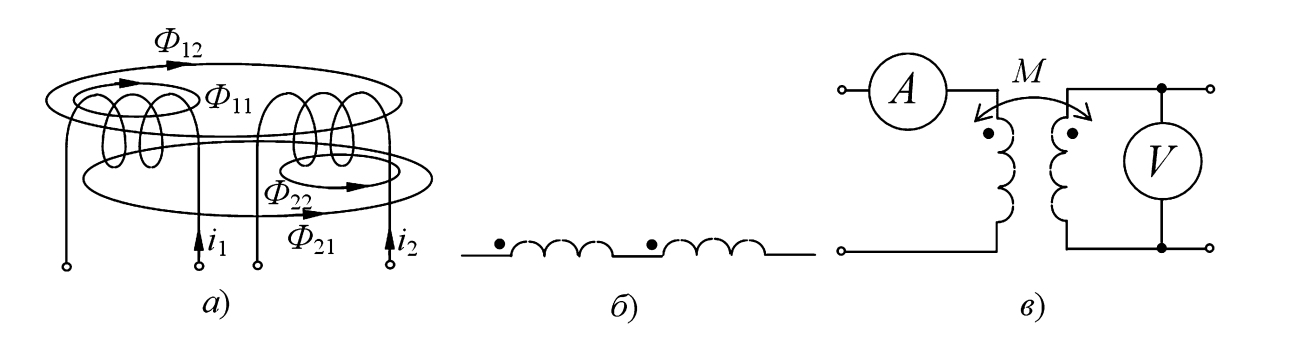
Рис. 1. Цепь со взаимной индуктивностью:
a — схема магнитных потоков;
б — разметка концов индуктивно связанных катушек;
в — определение взаимной индуктивности.

У второй катушки, аналогично, $\Phi_2 = \Phi_{22} + \Phi_{21}$. В итоге, полное потокосцепление первой катушки, имеющей $w_1$ витков, равно:

$$ \Psi_1 = w_1(\Phi_{11} + \Phi_{12}) \pm w_1\Phi_{21} = \Psi_{11} + \Psi_{12} \pm \Psi_{21} $$

Аналогично потокосцепление у второй катушки с $w_2$ витками:

$$ \Psi_2 = w_2(\Phi_{22} + \Phi_{21}) \pm w_2\Phi_{12} = \Psi_{22} + \Psi_{21} \pm \Psi_{12} $$

Часть потока от соседней катушки может оказаться со знаком плюс, когда потоки направлены согласно, или со знаком минус, когда потоки направлены встречно.

Потокосцепление $\Psi_{21}$ (создаваемое током $i_2$ и сцепленное с катушкой 1) пропорционально току $i_2$, а $\Psi_{12}$ (создаваемое током $i_1$ и сцепленное с катушкой 2) — току $i_1$, т. е.:

$$ \Psi_{21} = w_1\Phi_{21} = M_{21}i_2 $$
$$ \Psi_{12} = w_2\Phi_{12} = M_{12}i_1 $$

Коэффициент пропорциональности $M$ (измеряемый в Генри, Гн) называют взаимной индуктивностью. В линейных цепях доказывается справедливость принципа взаимности: $M = M_{21} = M_{12}$.

При изменении токов в катушках в них наводятся ЭДС. Полное потокосцепление катушек с учетом самоиндукции ($L_1$, $L_2$) и взаимной индукции ($M$) равно:

$$ \Psi_{1полн} = L_1i_1 \pm Mi_2 $$
$$ \Psi_{2полн} = L_2i_2 \pm Mi_1 $$

Согласно закону Фарадея, наведенные ЭДС равны:

$$ e_1 = -\frac{d\Psi_{1полн}}{dt} = -\frac{d(L_1i_1 \pm Mi_2)}{dt} = -L_1\frac{di_1}{dt} \mp M\frac{di_2}{dt} = e_{L1} \pm e_{M1} $$
$$ e_2 = -\frac{d\Psi_{2полн}}{dt} = -\frac{d(L_2i_2 \pm Mi_1)}{dt} = -L_2\frac{di_2}{dt} \mp M\frac{di_1}{dt} = e_{L2} \pm e_{M2} $$

Их называют соответственно $e_L$ — ЭДС самоиндукции, $e_M$ — ЭДС взаимоиндукции.

Коэффициент связи и энергия поля

Для оценки степени индуктивной связи вводят коэффициент связи $k_{св}$:

$$ k_{св} = \frac{M}{\sqrt{L_1 L_2}} $$

Коэффициент связи всегда меньше или равен единице ($k_{св} \le 1$). Значение $k_{св} = 1$ соответствует идеальной связи без потоков рассеяния (весь поток одной катушки сцеплен с другой), что является теоретической идеализацией. В реальных устройствах $k_{св} < 1$ из-за наличия потоков рассеяния ($\Phi_{11}$ и $\Phi_{22}$).

Магнитная энергия, накопленная в поле двух индуктивно связанных катушек, определяется выражением:

$$ W_M = \frac{L_1 i_1^2}{2} + \frac{L_2 i_2^2}{2} \pm Mi_1 i_2 $$

Знак «+» берется при согласном включении, «–» — при встречном.

Разметка катушек и экспериментальное определение M

Чтобы знать, согласно или встречно включены катушки, делают разметку их концов. На схемах начала обмоток (или концы с одинаковой полярностью наводимой ЭДС) условно обозначают точкой или звездочкой (рис. 1б). Если токи $i_1$ и $i_2$ одновременно входят в «точечные» зажимы, их потоки складываются (согласное включение). Если один ток входит, а другой выходит, потоки вычитаются (встречное).

Выполнить разметку концов и определить взаимную индуктивность можно экспериментально. Для этого включают обе катушки последовательно под напряжение $U$ (см. рис. 1в, но с последовательным соединением).

1. Метод последовательного включения

Если катушки включены согласно (начало одной к концу другой, и их потоки складываются), то уравнение напряжений для синусоидального тока будет иметь вид:

$$ u = iR_1 + L_1\frac{di}{dt} + M\frac{di}{dt} + iR_2 + L_2\frac{di}{dt} + M\frac{di}{dt} $$

В комплексном виде (для действующих значений):

$$ \dot{U} = \dot{I}R_1 + j\omega L_1 \dot{I} + j\omega M \dot{I} + \dot{I}R_2 + j\omega L_2 \dot{I} + j\omega M \dot{I} $$
$$ \dot{U} = \dot{I}[(R_1 + R_2) + j\omega(L_1 + L_2 + 2M)] = \dot{I} \cdot Z_{согл} $$

где $X_{согл} = \omega(L_1 + L_2 + 2M)$ — суммарное реактивное сопротивление.

Если катушки включены встречно (начало к началу или конец к концу, их потоки вычитаются):

$$ \dot{U} = \dot{I}[(R_1 + R_2) + j\omega(L_1 + L_2 — 2M)] = \dot{I} \cdot Z_{вст} $$

где $X_{вст} = \omega(L_1 + L_2 — 2M)$.

Примечание: Как видно, при встречном включении полное сопротивление цепи $Z_{вст}$ меньше, чем $Z_{согл}$ (поскольку $L_1 + L_2 — 2M < L_1 + L_2 + 2M$). Следовательно, при неизменном напряжении $U$ ток $I_{вст}$ будет больше, чем $I_{согл}$. Это и является критерием для разметки концов катушек: то включение, при котором ток больше, является встречным.

Для определения значения взаимной индуктивности, измерив $X_{согл}$ и $X_{вст}$ (например, методом вольтметра-амперметра-ваттметра), можно вычислить $M$:

$$ X_{согл} — X_{вст} = 4\omega M $$
$$ M = \frac{X_{согл} — X_{вст}}{4\omega} $$

2. Метод холостого хода

Можно определить взаимную индуктивность и другим способом (см. рис. 1в). На первую катушку подается напряжение $U_1$, измеряется ток $I_1$. На разомкнутых концах второй катушки измеряется напряжение $U_2$, которое равно ЭДС взаимоиндукции $E_{M2}$, пропорциональное току в первой катушке:

$$ \dot{U}_2 = \dot{E}_{M2} = j\omega M \dot{I}_1 $$

Тогда модуль $M$ можно найти как:

$$ M = \frac{U_2}{\omega I_1} $$

Расчет разветвленных цепей с взаимными индуктивностями

При расчете разветвленных цепей с взаимными индуктивностями составляют уравнения по законам Кирхгофа. Можно применять метод контурных токов, но нельзя применять классический метод узловых потенциалов.

Почему метод узловых потенциалов неприменим?
Классический метод узловых потенциалов основан на том, что ток в ветви зависит только от разности потенциалов на ее концах ($I = Y \cdot (V_a — V_b)$). В цепях с взаимной индуктивностью это не так. Напряжение на катушке $L_1$ зависит не только от тока $I_1$, но и от изменения тока $I_2$ в другой ветви ($u_1 = L_1(di_1/dt) \pm M(di_2/dt)$). Это нарушает базовую предпосылку метода узловых потенциалов. Для расчета таких цепей используют модифицированный метод узловых потенциалов или метод контурных токов.

Для примера составим уравнения по второму закону Кирхгофа для схемы, представленной на рисунке 2.

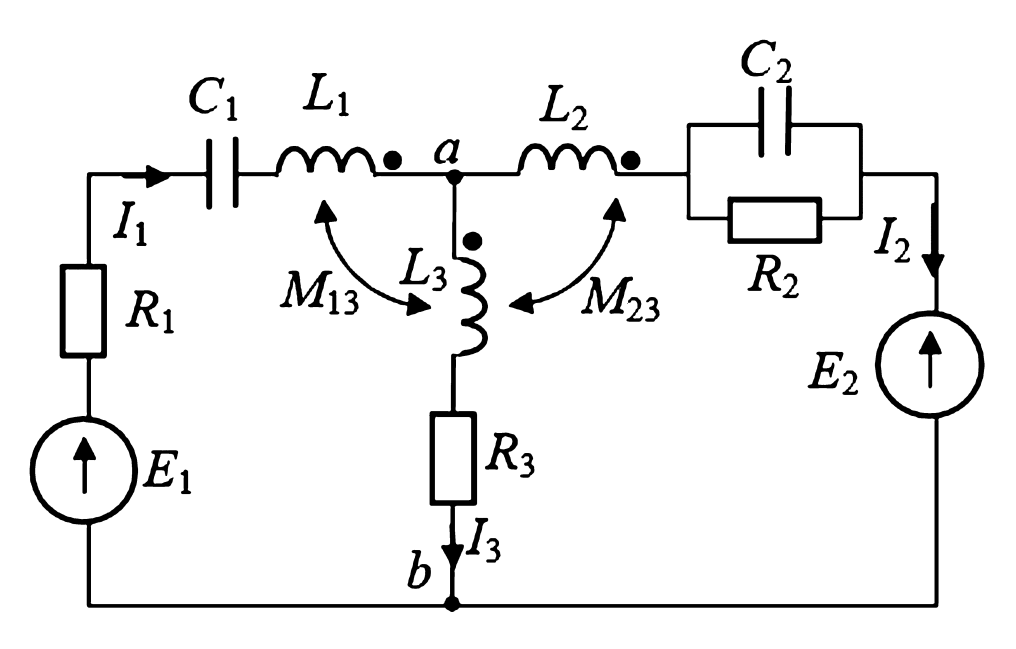
Рис. 2. Схема электрической цепи при наличии взаимных индуктивностей (L2 и L3 связаны).

Уравнения в комплексной форме (с учетом, что $\dot{I}_1 = \dot{I}_2 + \dot{I}_3$):

$$ \dot{I}_1 — \dot{I}_2 — \dot{I}_3 = 0 $$
$$ \dot{U}_{ab} = \dot{I}_2 Z_2 + \dot{I}_3 Z_3 \text{ (для внешнего контура)} $$

Или для внутренних контуров (предполагая источники $\dot{E}_1$ и $\dot{E}_2$):

$$ \dot{I}_1 Z_1 + \dot{I}_2 Z_2 + \dot{E}_1 = \dot{E}_2 \text{ (для левого контура)} $$
$$ \dot{I}_2 Z_2 — \dot{I}_3 Z_3 = \dot{E}_2 \text{ (для правого контура)} $$

В оригинальном примере (рис. 2) уравнения для контуров `ab1a` и `ab2a` (контурные токи $\dot{I}_{ab1}$ и $\dot{I}_{ab2}$) могли бы выглядеть так (приводя к системе):

$$ \dot{I}_1 Z_1 + (\dot{I}_1 — \dot{I}_3) Z_{13} = \dot{U}_{ab} — \dot{E}_1 $$
$$ \dot{I}_2 Z_2 + (\dot{I}_2 — \dot{I}_3) Z_{23} \pm j\omega M_{23} \dot{I}_3 = \dot{U}_{ab} — \dot{E}_2 $$
$$ \dot{I}_3 Z_3 + (\dot{I}_3 — \dot{I}_2) Z_{23} \pm j\omega M_{23} \dot{I}_2 + (\dot{I}_3 — \dot{I}_1) Z_{13} = \dot{U}_{ab} $$

(Примечание: точная система зависит от выбора контуров; исходный текст примера 3.25 был неполным и заменен на общее описание).

Важно обратить внимание на знаки. Если в катушках $L_2$ и $L_3$ токи направлены встречно (например, ток $\dot{I}_3$ входит в начало катушки $L_3$, а ток $\dot{I}_2$ — в конец $L_2$), то слагаемые с $M$ (в данном случае $Z_{23} = \pm j\omega M$) берутся со знаком минус.

Метод устранения индуктивных связей («Развязка»)

Чтобы упростить составление уравнений разветвленной цепи (и, в том числе, применить любой метод расчета, например, метод узловых потенциалов), применяют так называемое развязывание магнитно-связанных цепей.

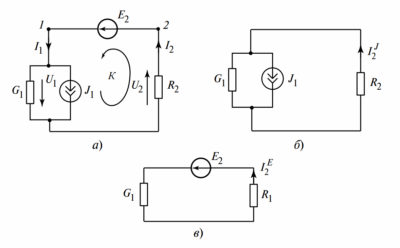
Если две ветви, имеющие взаимную индуктивность $M$, подключены к общему узлу 3 (рис. 3а), то, заменив эту схему на схему, представленную на рисунке 3б, получим полностью эквивалентную схему, но не содержащую индуктивных связей.

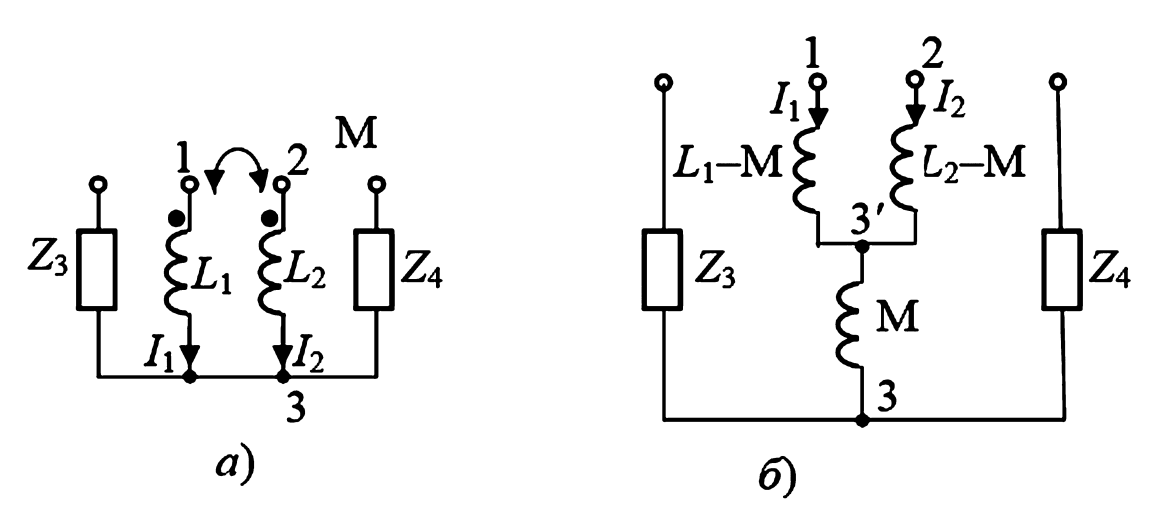
Рис. 3. «Развязка» индуктивно связанных цепей:
а — исходная схема (с индуктивной связью $M$);
б — преобразованная (эквивалентная) схема цепи (без индуктивной связи).

Действительно, для первой схемы (рис. 3а) с индуктивными связями (при согласном включении):

$$ \dot{U}_{13} = j\omega L_1 \dot{I}_1 + j\omega M \dot{I}_2 $$
$$ \dot{U}_{23} = j\omega L_2 \dot{I}_2 + j\omega M \dot{I}_1 $$

Для второй схемы (рис. 3б) без индуктивной связи (ток в общей ветви $\dot{I}_3 = \dot{I}_1 + \dot{I}_2$):

$$ \dot{U}_{13} = j\omega(L_1 — M)\dot{I}_1 + j\omega M (\dot{I}_1 + \dot{I}_2) = j\omega L_1 \dot{I}_1 + j\omega M \dot{I}_2 $$
$$ \dot{U}_{23} = j\omega(L_2 — M)\dot{I}_2 + j\omega M (\dot{I}_1 + \dot{I}_2) = j\omega L_2 \dot{I}_2 + j\omega M \dot{I}_1 $$

Уравнения идентичны. Необходимо следить за тем, чтобы токи $\dot{I}_1$ и $\dot{I}_2$ были направлены к общему узлу 3. Если при этом окажется, что катушки включены встречно, то знаки, стоящие перед $M$ в эквивалентной схеме (рис. 3б), меняются на противоположные (т. е. индуктивности ветвей будут $L_1 + M$, $L_2 + M$, а индуктивность общей ветви –$M$).

Пример 1. Расчет входного сопротивления

Задача: Определить входное сопротивление цепи (схема автотрансформатора), показанной на рисунке 4а.

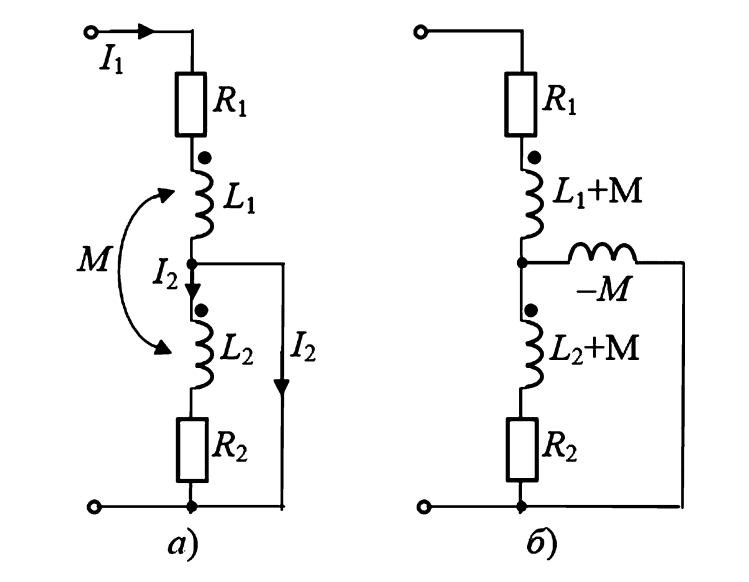
Рис. 4. Схема автотрансформатора:
а — исходная;
б — преобразованная методом «развязки».

Решение. Применим «развязывание», предполагая согласное включение (рис. 4б). Схема представляет собой две параллельные ветви, подключенные последовательно к $R_1$.

Ветвь 1: $Z_{в1} = j\omega M$

Ветвь 2: $Z_{в2} = R_2 + j\omega(L_2 — M)$

Индуктивность $L_1$ также «развязывается» на $L_1-M$ и $M$. Элемент $R_1$ и $(L_1-M)$ включены последовательно с параллельным участком.

Входное сопротивление $Z_{вх}$ равно:

$$ Z_{вх} = R_1 + j\omega(L_1 — M) + \frac{[R_2 + j\omega(L_2 — M)] \cdot (j\omega M)}{R_2 + j\omega(L_2 — M) + j\omega M} $$
$$ Z_{вх} = R_1 + j\omega(L_1 — M) + \frac{j\omega M [R_2 + j\omega(L_2 — M)]}{R_2 + j\omega L_2} $$

Трансформатор без ферромагнитного сердечника (Воздушный)

Трансформатор представляет собой техническое устройство, использующее явление взаимоиндукции для передачи энергии из одной цепи в другую, как правило, с изменением уровней напряжения и тока. Это позволяет гальванически разделить цепи, преобразовать напряжение и токи, согласовать сопротивления.

Обычно силовой трансформатор содержит ферромагнитный сердечник для концентрации магнитного потока (достижения $k_{св} \approx 1$), однако при этом он становится нелинейным устройством (из-за кривой намагничивания $B(H)$). Рассмотрим линейный трансформатор без ферромагнитного сердечника (рис. 5а), называемый иногда воздушным трансформатором.

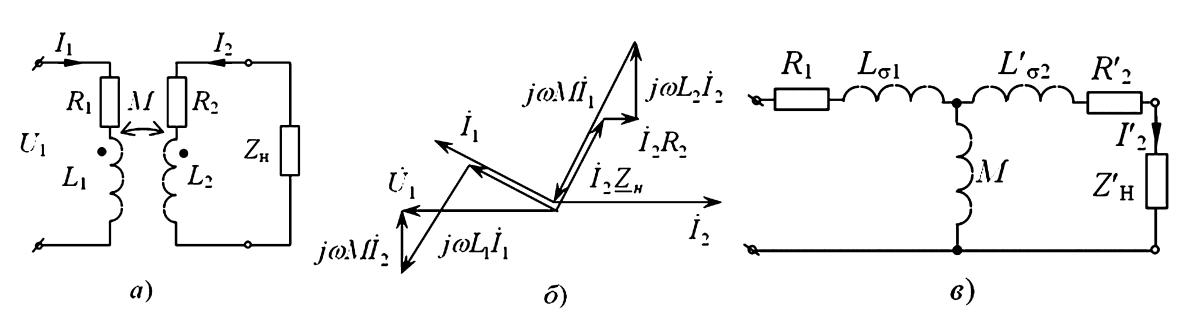
Рис. 5. Трансформатор:
а — схема;
б — векторная диаграмма;
в — приведенная схема трансформатора (Т-образная).

Запишем уравнения трансформатора в комплексной форме (по второму закону Кирхгофа):

Для первичной цепи (контура):

$$ \dot{U}_1 = \dot{I}_1 R_1 + j\omega L_1 \dot{I}_1 + j\omega M \dot{I}_2 $$

Для вторичной цепи (контура):

$$ 0 = \dot{I}_2 R_2 + j\omega L_2 \dot{I}_2 + \dot{I}_2 Z_н + j\omega M \dot{I}_1 $$

Перегруппируем:

$$ \dot{U}_1 = \dot{I}_1 (R_1 + j\omega L_1) + \dot{I}_2 (j\omega M) $$
$$ 0 = \dot{I}_1 (j\omega M) + \dot{I}_2 (R_2 + j\omega L_2 + Z_н) $$

Решая эти уравнения, определим входное сопротивление $Z_1 = \dot{U}_1 / \dot{I}_1$. Из второго уравнения выразим $\dot{I}_2$:

$$ \dot{I}_2 = — \frac{j\omega M \dot{I}_1}{R_2 + j\omega L_2 + Z_н} $$

Подставим в первое уравнение:

$$ \dot{U}_1 = \dot{I}_1 (R_1 + j\omega L_1) — \frac{(j\omega M)^2 \dot{I}_1}{R_2 + j\omega L_2 + Z_н} $$
$$ Z_{вх} = \frac{\dot{U}_1}{\dot{I}_1} = (R_1 + j\omega L_1) + \frac{(\omega M)^2}{R_2 + j\omega L_2 + Z_н} $$

Входное сопротивление состоит из собственного сопротивления первичной обмотки $Z_1 = R_1 + j\omega L_1$ и внесенного сопротивления $Z_{вн}$:

$$ Z_{вн} = R_{вн} + jX_{вн} = \frac{(\omega M)^2}{R_2 + j\omega L_2 + Z_н} $$

Это $Z_{вн}$ — сопротивление, вносимое из вторичной цепи в первичную. При уменьшении сопротивления нагрузки $Z_н$ (ток $\dot{I}_2$ увеличивается), увеличивается вносимое сопротивление. Обратите внимание, что $X_{вн}$ часто получается со знаком минус (имеет емкостный характер), что уменьшает индуктивное сопротивление первичной обмотки и приводит к увеличению тока $\dot{I}_1$. То есть, увеличение тока $\dot{I}_2$ автоматически приводит к увеличению тока $\dot{I}_1$.

Баланс мощности

Определим комплексную мощность, обусловленную взаимной индукцией. Мощность, передаваемая из-за ЭДС $e_{M1} = -j\omega M \dot{I}_2$ в первичную цепь:

$$ \dot{S}_{M1} = \dot{E}_{M1} \dot{I}_1^* = (-j\omega M \dot{I}_2) \dot{I}_1^* = -j\omega M \dot{I}_2 \dot{I}_1^* $$

Мощность, передаваемая из-за ЭДС $e_{M2} = -j\omega M \dot{I}_1$ во вторичную цепь:

$$ \dot{S}_{M2} = \dot{E}_{M2} \dot{I}_2^* = (-j\omega M \dot{I}_1) \dot{I}_2^* $$

Активная и реактивная мощности (при $I_1=I_1 e^{j\phi_1}$, $I_2=I_2 e^{j\phi_2}$):

$$ P_{1M} = \omega M I_1 I_2 \sin(\phi_1 — \phi_2) = — P_{2M} $$
$$ Q_{1M} = \omega M I_1 I_2 \cos(\phi_1 — \phi_2) $$

Если $P_{1M} > 0$, то активная мощность передается из первичной обмотки во вторичную.

Векторная диаграмма трансформатора

На рисунке 5б приведена векторная диаграмма трансформатора. Построение выполняется в следующем порядке:

Отложим по вещественной оси ток $\dot{I}_2$.
Под углом $\phi_н$ к $\dot{I}_2$ откладываем напряжение на нагрузке $\dot{U}_н = \dot{I}_2 Z_н$.
Строим падение напряжения на активном сопротивлении вторичной обмотки $\dot{I}_2 R_2$ (параллельно вектору $\dot{I}_2$).
Строим падение напряжения на индуктивности $j\omega L_2 \dot{I}_2$ (перпендикулярно $\dot{I}_2$, опережая на 90°).
В соответствии со вторым уравнением трансформатора (в форме $\dot{E}_{M2} + \dot{I}_2 R_2 + j\omega L_2 \dot{I}_2 + \dot{I}_2 Z_н = 0$), сумма этих напряжений равна ЭДС взаимоиндукции $\dot{E}_{M2} = -j\omega M \dot{I}_1$. Вектор $\dot{E}_{M2}$ замыкает многоугольник напряжений (направлен к началу координат).
Определив $\dot{E}_{M2}$, можно определить направление тока $\dot{I}_1$, так как вектор $\dot{E}_{M2}$ отстает от $\dot{I}_1$ на 90° (умножение на $-j\omega M$). (Или, как в исходном тексте, $\dot{U}_{M2} = j\omega M \dot{I}_1$ опережает $\dot{I}_1$ на 90°).
Зная направление $\dot{I}_1$, строим $\dot{I}_1 R_1$ (параллельно $\dot{I}_1$) и $j\omega L_1 \dot{I}_1$ (перпендикулярно $\dot{I}_1$).
Добавляем вектор ЭДС $\dot{E}_{M1} = -j\omega M \dot{I}_2$ (отстает от $\dot{I}_2$ на 90°).
Сумма векторов $\dot{I}_1 R_1$, $j\omega L_1 \dot{I}_1$ и $\dot{E}_{M1}$ (или $\dot{I}_1 Z_1 + \dot{U}_{M2}$) в соответствии с первым уравнением дает $\dot{U}_1$.

Приведенная схема замещения (Т-схема)

Соединив нижние концы обмоток трансформатора (при этом ничего не изменится) и применив «развязывание» индуктивно-связанных цепей (как на рис. 3), получим Т-образную схему замещения трансформатора без индуктивных связей (рис. 5в).

Часто используется приведенная схема замещения, в которой, кроме «развязывания», вторичная цепь приведена к первичной. Параметры вторичной цепи ($R_2$, $L_2$, $Z_н$) умножаются на квадрат коэффициента трансформации $k^2$:

$$ Z’_н = k^2 Z_н $$
$$ R’_2 = k^2 R_2 $$
$$ L’_2 = k^2 L_2 $$

При этом «приведенные» ток и напряжение равны:

$$ \dot{I}’_2 = \dot{I}_2 / k $$
$$ \dot{U}’_2 = k \dot{U}_2 $$

Выбирая $k = U_{1xx} / U_{2xx} \approx w_1 / w_2$ (коэффициент трансформации в режиме холостого хода), получим схему, где $\dot{U}’_2 \approx \dot{U}_1$ и $\dot{I}’_2 \approx \dot{I}_1$.

При этом в Т-схеме (рис. 5в) индуктивность $L_{S1} = L_1 — M$ называется индуктивностью рассеяния первичной обмотки, а $L’_{S2} = k^2(L_2 — M)$ — приведенной индуктивностью рассеяния вторичной обмотки. Ветвь $j\omega M$ (или $j\omega M’$) называется ветвью намагничивания.

Трансформатор часто используют как согласующий элемент. В приведенной схеме (рис. 5в), пренебрегая сопротивлениями $R_1$, $R’_2$ и индуктивностями рассеяния $L_{S1}$, $L’_{S2}$, и считая сопротивление $j\omega M$ (намагничивания) достаточно большим (т.е. $I_{1xx} \approx 0$), можно увидеть, что входное сопротивление трансформатора:

$$ Z_{вх} \approx Z’_н = k^2 Z_н = \left(\frac{w_1}{w_2}\right)^2 Z_н $$

Иногда используют понятие «идеальный трансформатор», у которого элементы $R_1, R_2, L_{S1}, L_{S2}$ равны нулю (нет потерь и рассеяния) и $M \to \infty$ (и $L_1, L_2 \to \infty$, но $k$ = const). Тогда $U_1 = kU_2$, $I_1 = I_2 / k$ и $Z_{вх} = k^2 Z_н$.

Преимущества и недостатки индуктивной связи

Явление взаимной индукции имеет как фундаментальные преимущества, так и существенные недостатки, в зависимости от области применения.

Преимущества

Гальваническая развязка: Позволяет передавать энергию между цепями без прямого электрического контакта, что критически важно для безопасности (в медицинском оборудовании) и для устранения «земельных петель» в измерительных системах.
Трансформация напряжений и токов: Основа работы трансформаторов, позволяющая эффективно повышать напряжение для ЛЭП (снижая потери) и понижать его для потребителей.
Согласование импедансов: Как показано выше, $Z_{вх} = k^2 Z_н$. Это позволяет согласовать низкоомную нагрузку (например, динамик) с высокоомным выходом усилителя для передачи максимальной мощности.
Беспроводная передача энергии: Современные системы (Qi, A4WP) используют магнитную индукцию для зарядки устройств.

Недостатки (Паразитная связь)

Электромагнитные помехи (EMI): Взаимная индукция является одной из главных причин перекрестных помех в электронике. Сильноточный кабель может наводить помехи в чувствительном сигнальном кабеле, проложенном рядом.
Сложность анализа: Как видно из статьи, расчет цепей с $M$ значительно сложнее, чем без нее.
Потоки рассеяния: Неидеальный коэффициент связи ($k < 1$) приводит к появлению индуктивностей рассеяния, которые ограничивают КПД и частотные характеристики трансформаторов.
Проблемы в ВЧ-технике: На высоких частотах даже короткие параллельные дорожки на печатной плате обладают заметной взаимной индуктивностью, что требует сложного моделирования (EMC/EMI).

Сравнение согласного и встречного включения

Разница в подключении индуктивно связанных катушек кардинально меняет параметры итоговой цепи.

Характеристика	Согласное включение	Встречное включение
Направление потоков	Магнитные потоки $\Phi_1$ и $\Phi_2$ суммируются.	Магнитные потоки $\Phi_1$ и $\Phi_2$ вычитаются.
Эквивалентная индуктивность (при послед. соед.)	$L_{экв} = L_1 + L_2 + 2M$	$L_{экв} = L_1 + L_2 — 2M$
Накопленная энергия поля	$W_M = \frac{L_1 i_1^2}{2} + \frac{L_2 i_2^2}{2} + Mi_1 i_2$	$W_M = \frac{L_1 i_1^2}{2} + \frac{L_2 i_2^2}{2} — Mi_1 i_2$
Реактивное сопротивление (при послед. соед.)	$X_{согл} = \omega(L_1 + L_2 + 2M)$ (Максимальное)	$X_{вст} = \omega(L_1 + L_2 — 2M)$ (Минимальное)
Ток в цепи (при U=const, послед. соед.)	Минимальный (т.к. $Z$ максимальное)	Максимальный (т.к. $Z$ минимальное)

Интересные факты о взаимной индуктивности

Беспроводная зарядка — это $M$: Все современные беспроводные зарядки (стандарт Qi) работают исключительно на принципе взаимной индуктивности между катушкой в базе и катушкой в устройстве.
Мечта Теслы: Никола Тесла был одержим идеей передачи энергии на большие расстояния через индукцию (Резонансная индуктивная связь), что, по сути, является оптимизированной взаимной индукцией.
$M$ может быть «отрицательной»: Взаимная индуктивность $M$ по определению всегда положительна. Однако в уравнениях цепи (например, $L_1 \pm M$) знак «минус» (встречное включение) можно математически представить как $L_1 + (-M)$, где $-M$ учитывает ориентацию обмоток.
«Точки» — это условность: Маркировка точками (dot convention) — это лишь один из способов учесть полярность. В сложных 3D-моделях для EMC-анализа используются матрицы парциальных индуктивностей, где $M_{ij}$ — взаимная индуктивность между $i$-м и $j$-м проводником.
Индуктивность рассеяния — враг энергетика: Именно индуктивность рассеяния ($L_S = L_1 — M$) в силовых трансформаторах вызывает падение напряжения под нагрузкой и ограничивает ток короткого замыкания.
Дроссели на основе $M$: Синфазные дроссели (Common Mode Choke), используемые во всех блоках питания, — это две катушки на одном сердечнике. Они имеют высокую взаимную индуктивность ($k \to 1$) и включены так, что для полезного (дифференциального) сигнала их потоки вычитаются ($L_{экв} \approx L_S$), а для помехи (синфазной) — складываются ($L_{экв} \approx L+M$), эффективно подавляя ее.
«Генри» в честь Генри: Единица измерения индуктивности «Генри» (Гн) названа в честь Джозефа Генри, который открыл самоиндукцию и взаимную индукцию независимо от Майкла Фарадея.

FAQ: Часто задаваемые вопросы

1. Что физически означает коэффициент связи $k$?

Коэффициент связи $k$ — это безразмерная величина (от 0 до 1), показывающая, какая доля магнитного потока, созданного одной катушкой, пронизывает (сцепляется) витки второй катушки. $k=1$ — идеальная связь (весь поток общий, нет рассеяния). $k=0$ — связи нет (катушки бесконечно далеко или ортогональны).

2. Почему нельзя использовать метод узловых потенциалов (МУП) для цепей с $M$?

Классический МУП требует, чтобы ток в ветви был функцией только потенциалов на ее концах (например, $I = V/Z$). Взаимная индукция нарушает это: напряжение на катушке $L_1$ зависит от тока в другой ветви (через $M \cdot di_2/dt$). Существуют модифицированные МУП, которые обходят это, но классический — неприменим.

3. Что такое «развязка» цепи и зачем она нужна?

«Развязка» — это метод математического преобразования схемы. Мы заменяем две индуктивно связанные катушки на три катушки без индуктивной связи (Т-схема, см. Рис. 3б). Новая схема полностью эквивалентна старой, но в ней нет $M$. Это позволяет рассчитывать ее любыми классическими методами, включая МУП.

4. В чем разница между «воздушным» и силовым трансформатором?

Главное отличие — в сердечнике. Воздушный (без сердечника или на диэлектрическом) — линейное устройство, $k$ очень мал (0.01-0.2), используется в ВЧ-технике (радио). Силовой (с ферромагнитным сердечником) — нелинейный, $k$ близок к 1 (0.95-0.99), используется для передачи энергии на 50/60 Гц.

5. Что такое «внесенное сопротивление»?

Это «кажущееся» сопротивление, которое «видит» источник в первичной цепи из-за того, что к вторичной цепи подключена нагрузка. Энергия, потребляемая нагрузкой $Z_н$ во вторичной цепи, «отражается» в первичную цепь как дополнительное сопротивление $Z_{вн} = (\omega M)^2 / (Z_2 + Z_н)$.

6. Как на практике определить начала обмоток (поставить «точки»)?

Помимо метода с вольтметром/амперметром (сравнение $I_{согл}$ и $I_{вст}$), можно использовать импульсный метод. Подать на одну обмотку импульс постоянного тока (например, от батарейки) и посмотреть полярность ЭДС на другой обмотке стрелочным вольтметром. Если при замыкании цепи 1 вольтметр на цепи 2 отклоняется в ту же сторону, что и при прямом подключении к батарейке, то «плюс» батарейки и «плюс» вольтметра — одноименные зажимы («точки»).

7. Что такое индуктивность рассеяния?

Это часть индуктивности обмотки, связанная с магнитным потоком, который не участвует во взаимной индукции и замыкается только вокруг своей обмотки (потоки $\Phi_{11}$ и $\Phi_{22}$ на Рис. 1а). В Т-схеме (Рис. 5в) она представлена $L_{S1} = L_1 — M$ и $L_{S2} = L_2 — M$. Это паразитный, но неизбежный параметр.

Заключение

Взаимная индуктивность является фундаментальным понятием в теории электрических цепей, описывающим неразрывную связь между электрическими и магнитными явлениями. Понимание принципов расчета цепей с индуктивными связями критически важно для проектирования широкого спектра устройств — от миниатюрных радиочастотных контуров и беспроводных зарядных устройств до мощных силовых трансформаторов, питающих города.

Методы анализа, такие как использование законов Кирхгофа с учетом ЭДС взаимоиндукции и эквивалентное преобразование («развязка») цепей, позволяют свести сложную задачу анализа магнитно-связанных систем к более привычным методам расчета. Учет как полезных (трансформация), так и паразитных (помехи) аспектов взаимной индукции является ключевой компетенцией инженера-электрика.

Нормативные документы (ГОСТ)

ГОСТ 34845-2021 «Трансформаторы силовые. Термины и определения.» (Действующий, введен взамен ГОСТ 16110-82).
ГОСТ Р 52002-2003 «Электротехника. Термины и определения. Основные понятия.» (Действующий).
ГОСТ 8.417-2002 «Государственная система обеспечения единства измерений (ГСИ). Единицы величин.» (Определяет единицы СИ, включая Генри, Вебер, Тесла).

Характеристика	Согласное включение	Встречное включение
Направление потоков	Магнитные потоки \(\Phi_1\) и \(\Phi_2\) суммируются.	Магнитные потоки \(\Phi_1\) и \(\Phi_2\) вычитаются.
Эквивалентная индуктивность (при послед. соед.)	\(L_{экв} = L_1 + L_2 + 2M\)	\(L_{экв} = L_1 + L_2 — 2M\)
Накопленная энергия поля	\(W_M = \frac{L_1 i_1^2}{2} + \frac{L_2 i_2^2}{2} + Mi_1 i_2\)	\(W_M = \frac{L_1 i_1^2}{2} + \frac{L_2 i_2^2}{2} — Mi_1 i_2\)
Реактивное сопротивление (при послед. соед.)	\(X_{согл} = \omega(L_1 + L_2 + 2M)\) (Максимальное)	\(X_{вст} = \omega(L_1 + L_2 — 2M)\) (Минимальное)
Ток в цепи (при U=const, послед. соед.)	Минимальный (т.к. \(Z\) максимальное)	Максимальный (т.к. \(Z\) минимальное)

Цепи с взаимными индуктивностями: Теоретический анализ и методы расчета